2. Интерференция света от двух точечных источников.

Свет от двух когерентных источников, находящихся на расстоянии друг от друга, падает на экран, на котором наблюдается система интерференционных полос. Расстояние от источников до экрана равно.

Найти координаты максимумов и минимумов интенсивности на экране и расстояние между ними.

Разность хода соответствует разности фаз. Из условия максимума интенсивностиможно найти координаты, где будут расположены полосы наибольшей интенсивности.Рис.1 Схема опыта Юнга

или,.

Минимумы (тёмные полосы) будут располагаться там, где

при  = (2q+1), то есть

,

Расстояние между двумя светлыми или тёмными полосами составляет:

, и величина называется шириной интерференционной полосы.

Заметим, что для тех точек, куда волны приходят в фазе, выполняется условие , то есть на длинеукладывается чётное число полуволн или целое число волн. При интерференции волны усиливают друг друга. В этих точках наблюдается максимум интенсивности и при равных амплитудах волн суммарная амплитуда в 2 раза больше, а интенсивность в 4 раза больше интенсивности каждой из волн.

В тех точках, куда волны приходят в противофазе, и выполняется условие , то есть на длинеукладывается нечётное число полуволн или полуцелое число волн, и волны гасят друг друга.

Из закона сохранения энергии следует, что уменьшение энергии в области тёмных полос должно компенсироваться увеличением энергии в области светлых полос.Если , результирующая интенсивность в интерференционной картине описывается выражением: (См. рис.2 распределение интенсивности)

Рис.2. Простейшие интерференционные схемы

Опыт Юнга

Проведённый расчёт интерференционной картины является общим для многих интерференционных схем, которые сводятся к эквивалентной схеме из двух когерентных источников.

3. Простейшие интерференционные схемы.

Р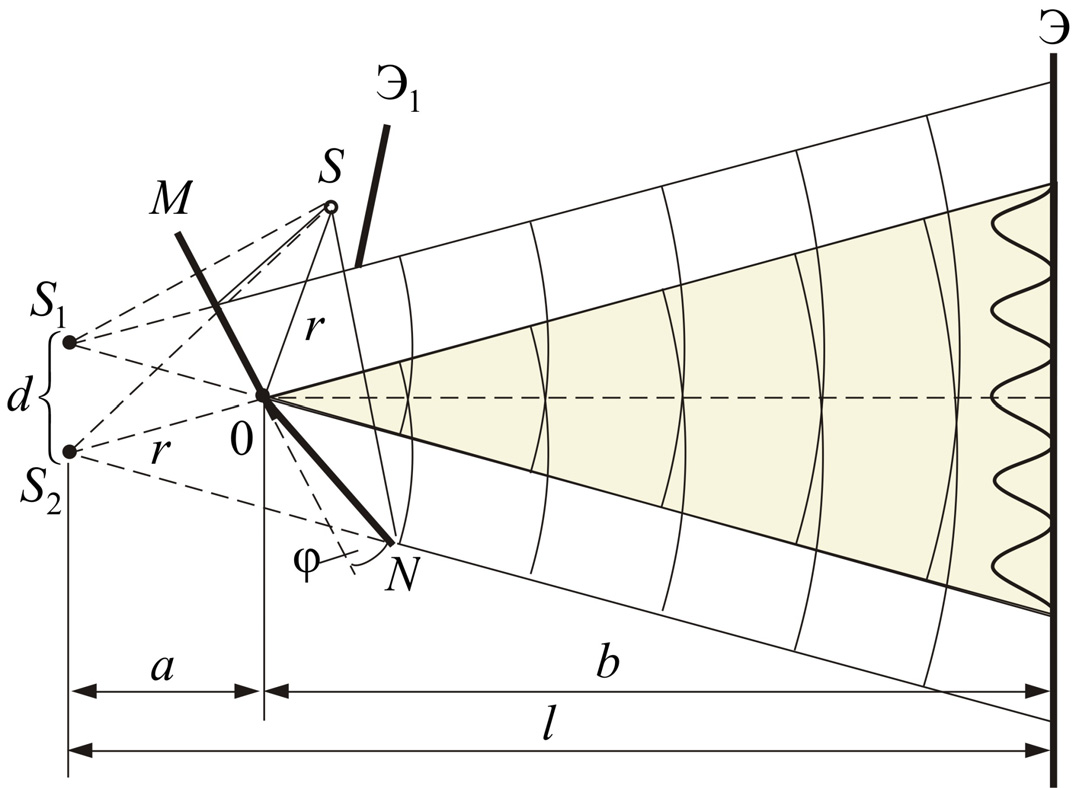ассмотрим на примере ( бипризма Френеля (рис.3), бизеркала Френеля (рис.4), билинза Бийё (рис.5).

.

Рис.3 Рис.4

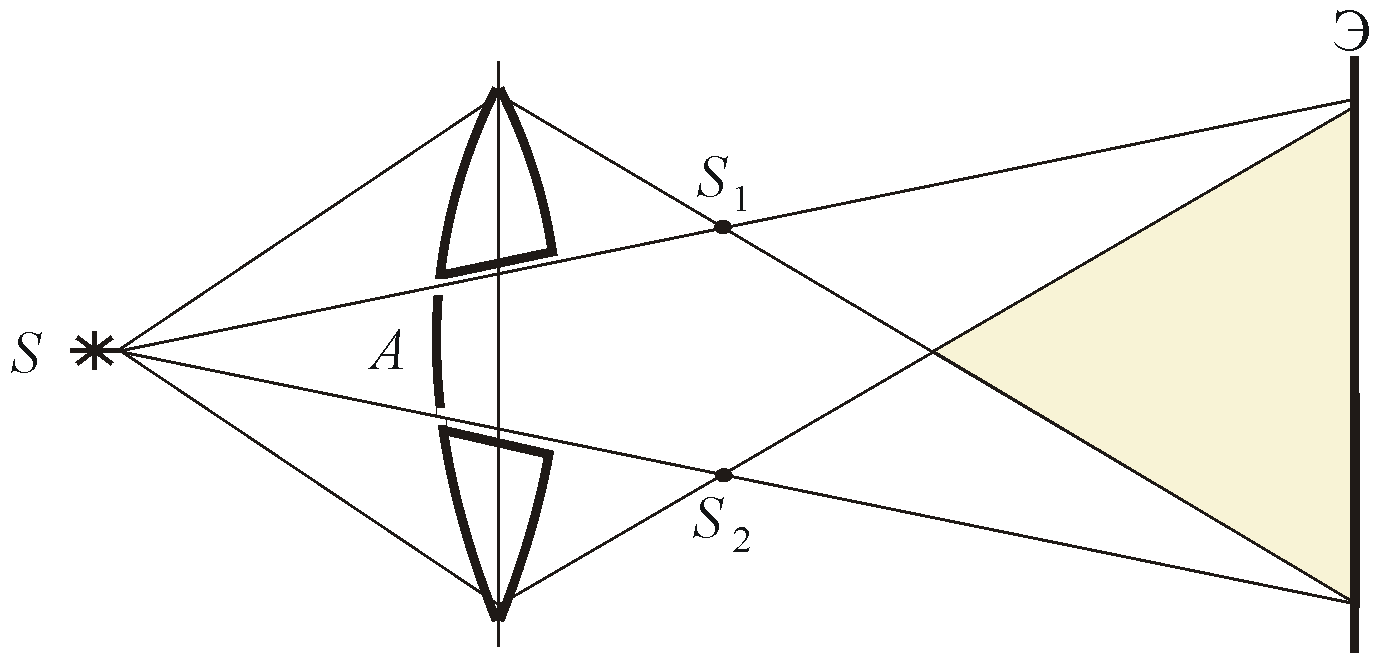
Рис.5

Д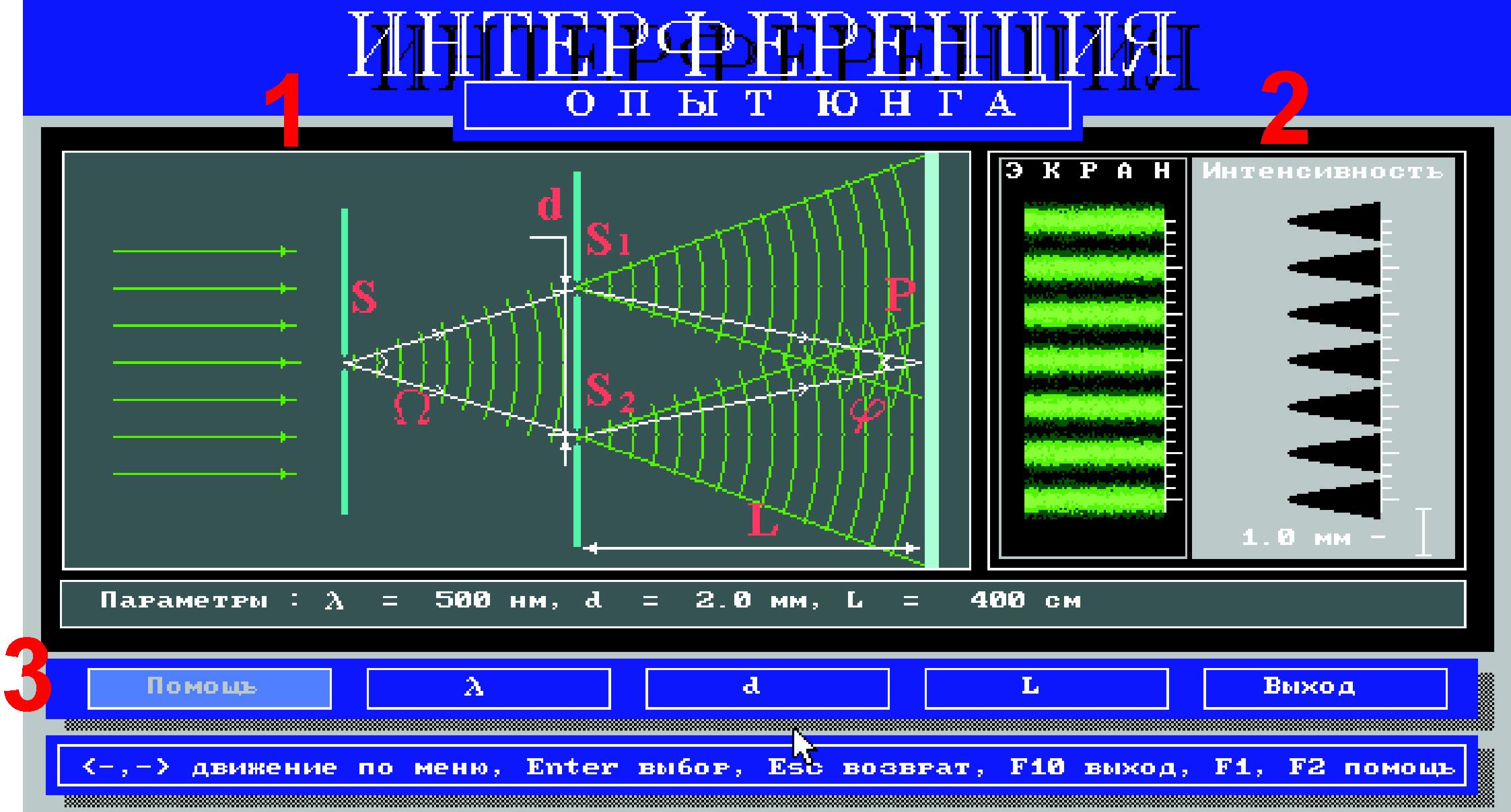ЕМОНСТРАЦИЯ КОМПЬЮТЕРНОЙ МОДЕЛИ (ПО ВЫБОРУ ПРЕПОДАВАТЕЛЯ)

Рис.6

Компьютерная программа «Интерференция» иллюстрирует основные законы интерференции световых волн. Моделируются различные широко известные двухлучевые оптические интерференционные схемы: oпыт Юнга, бизеркала Френеля, интерферометр Майкельсона, интерференция в плоскопараллельной пластинке и др. Предусмотрена возможность изменения параметров интерференционных схем, а также длины волны света.

На рис. 6 приведен вид экрана в данной программе. Цифра 1 соответствует виду интерференционной картины, цифра 2- графику распределения интенсивности, цифра 3 - окно изменяемых параметров интерференционной схемы.

НАПРИМЕР: В схеме опыта Юнга программа позволяет, меняя параметры схемы: d - расстояние между источниками (щелями) и ,L -расстояние от щелей до экрана наблюдения и длину волны , следить за изменением ширины интерференционных полос и интенсивности на экране.