Билет 14.

Вопрос 2.

Свободные гармоничесие колебания. Колебания с одной степенью свободы. Сложения колебаний. Биения. Фигуры Лиссажу.

Среди различных процессов втречаются периодически повторяющиеся (колебания). Колебательный процесс может возникнуть за счёт внешней силы, которая вывела систему из равнвесия и перестала действовать, а колебания происходят под действием только внутренних сил, без участия внешних. Такие колебания наз. собственными. Колебания содной степенью свободы– это колебания при которых движения системы можно описать одним независимым параметром (координатой). Пример: колебания математического маятника, колебания физического маятника (твёрдое тело, подвешенное за точку и способное колебаться вокруг оси, не проходящей через ц. м.), колебания груза на пружинке.

Уравнения для физического маятника: J=–mgasin–mga, приведённая длинна физического маятника, равна длинне математического маятника с тем же периодом –l=J₀+ma²/ma.T=, решение этого уравнения:=₀cos(t+),₀,определяются начальными условиями,– параметр системы.Колебания происходящие по законуsinуса илиcosинуса наз.гармоническими.

Сложение гармонических колебаний одинаковой частоты. x₁=A₁cos(t+₁),x₂=A₂cos(t+₂). Представим в комплексной форме: x=x₁+x₂=A₁e^i(t+1)+ A₂e^i(t+2)=e^it(A₁e^i1+A₂e^i2), A₁e^i1+A₂e^i2=Ae^i, A²=A₁²+A₂²+2 A₁A₂cos(₁–₂,), tg =(A₁sin₁+A₂sin₂)/(A₁cos₁+A₂cos₂)  x=x₁+x₂=Ae^i(t+)  x=Acos( t–).

Сложения гармонических колебаний с близкими частотами. x₁=A₁cos(₁t+₁),x₂=A₂cos(₂t+₂). Каждое из колебаний представим в комплексной форме, а сложение будем производить векторно. ПустьA₁>A₂.Cуммой двух колебаний с близкими частотами является колебание с изменяющейся амплитудой (от А₁–А₂до А₁+А₂) и с частотой |₁–₂|. Колебания амплитуды с частотой=|₁–₂| называются с биениями, а частота– частотой биения.

Фигуры Лиссажу.

Билет 15.

Вопрос 1.

Уравнение движения в релятивистской меканике. Импульс и энергия. Энергия покоя.

Уравнение движения в релятивистской механике

Полную силу F, действующую на частицу, можно разложить на тангенциальную и нормальную компоненты:

Каждая из компонент силы создает в соответствующем направлении ускорение, которое определяется инертностью тела в этом направлении

;

Если ввести единичные векторы: и, то эти уравнения можно записать в виде:

Левую часть этого уравнения можно упростить.

Принимая во внимание, что:, и представляя формулу:

в видезаменимна

, прямым дифференцированием проверяем равенство, с помощью которого левую часть упрощаемого уравнения преобразуем к виду:

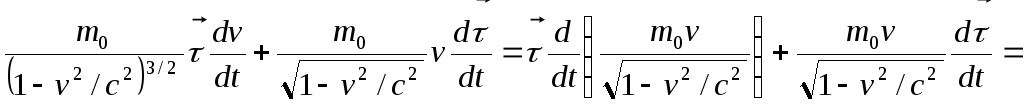
, где-скорость частицы.

Таким образом, уравнение движения в релятивистской механике:

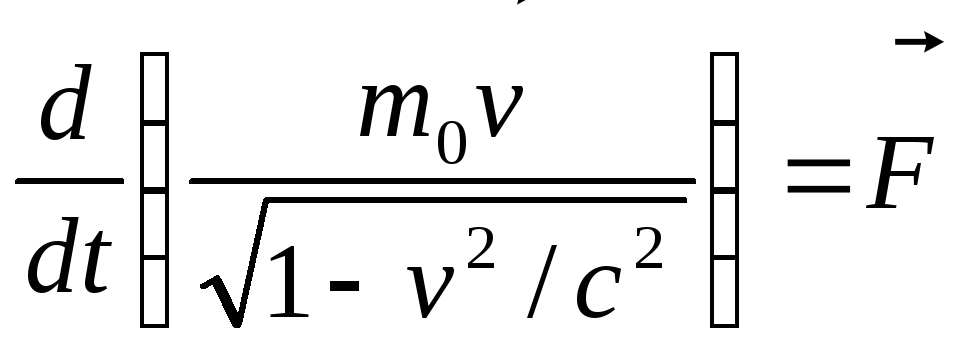, или- релятивистский импульс.

Импульс материальной точки – вектор, равный произведению массы точки на ее скорость:

Энергия покоя

получается изпри

Вопрос 2.

Затухающие колебания. Показатель (коэффициэнт) затухания, логарифмический декремент, добротность.

Затухающие колебания. Воспользуемся наиболее простым случаем «жидкого» или «вязкого» трения, когда сила трения направлениа противоположно скорости и пропорциональна скорости. Колебания при наличии трения становятся затухающими:

. - коэффициент трения,

Решение этого уравнения удобно искать в виде

. Учитывая, что,

, находим

Решение этого уравфнения:, где

, (*)

При не очень больших

- вещественная величина и

- гармоническая функция

Вещественная часть колебания, описываемого равенством (*), представляется формулой:

Отсюда видно, что амплитуда колебаний уменьшается в е=2,7раза в течение времени

-время затухания, а- показатель (коэффициент, декремент) затухания.

Всё выше написанное относится к случаю не очень больщих коэффициентов трения и когда – действительное число.

Логарифмический декремент

, ,

- логарифмический декремент

Другая интерпретация:

Приамплитуда уменьшается вераз, поэтому

Добротность. Q=A_рез/А_ст=₀/2=2/2T=/, т. к._рез²=₀²+2².