
СЕМИНАР 1 Кинематика точки Вектор скорости, модуль вектора скорости, вектор ускорения, модуль вектора ускорения.
![]()
![]()
![]()
![]()
![]()
![]()
Тангенциальное ускорение.
![]() - тангенциальное ускорение
– производная от модуля скорости по
времени. Для нахождения тангенциального
ускорения сначала находим модуль
скорости как функцию времени и затем
дифференцируем эту функцию по времени.
- тангенциальное ускорение
– производная от модуля скорости по
времени. Для нахождения тангенциального
ускорения сначала находим модуль
скорости как функцию времени и затем
дифференцируем эту функцию по времени.
Нормальное ускорение.
Вектору скорости присущи два
атрибута: модуль и направление в
пространстве. Производная вектора
скорости по времени, может быть
представлена в виде суммы двух слагаемых.
Одно из этих слагаемых – это тангенциальное
(касательное) ускорение. Другое слагаемое
характеризует быстроту изменения
направления скорости – это нормальное
ускорение. Таким образом, имеем
![]() .
.
В соответствии с теоремой
Пифагора, получаем полезную формулу
![]() .
.
Радиус кривизны траектории.
Можно показать, что нормальное
ускорение, характеризующее быстроту
изменения направления скорости, связано
с величиной скорости формулой
![]() .
Здесь ρ – радиус кривизны траектории.
Отсюда получаем
.
Здесь ρ – радиус кривизны траектории.
Отсюда получаем
![]() .
Именно такой формулой будем пользоваться
для нахождения радиуса кривизны
траектории в этом разделе.
.
Именно такой формулой будем пользоваться
для нахождения радиуса кривизны
траектории в этом разделе.
Вращательное движение твердого тела вокруг постоянной оси
Угловая скорость, угловое ускорение.
При описании вращательного
движения твердого тела, наряду с векторами
перемещения любых точек твердого тела,
вводят единый для всех точек вектор
элементарного угла поворота
![]() .
Кроме линейных скоростей точек твердого
тела, вводят единую для всех точек
угловую скорость
.
Кроме линейных скоростей точек твердого
тела, вводят единую для всех точек
угловую скорость
![]() .
Угловое ускорение
.
Угловое ускорение
![]() .
Формула, связывающая величину угловой
скорости и частоты вращения
.
Формула, связывающая величину угловой
скорости и частоты вращения![]() .
.
Связь угловых характеристик движения с линейными.
![]() ,
,![]() ;
;
![]() ,
,
![]() ;
;
![]() ,
,
![]() .
Здесь
.
Здесь
![]() - радиус – вектор, рассматриваемой точки
твердого тела, начинающийся в любой
точке оси вращения; R
– расстояние от рассматриваемой точки
твердого тела до оси вращения.
- радиус – вектор, рассматриваемой точки
твердого тела, начинающийся в любой
точке оси вращения; R
– расстояние от рассматриваемой точки
твердого тела до оси вращения.
Кинематика относительного движения (Галилей, Кориолис)
![]() ,
,
![]() - скорость и ускорение
материальной точки относительно
S - СО;
- скорость и ускорение
материальной точки относительно
S - СО;
![]() ,
,
![]() -
скорость и ускорение материальной точки
относительно S
- СО;
-
скорость и ускорение материальной точки
относительно S
- СО;
![]() - радиус-вектор материальной точки
относительно S
- СО;
- радиус-вектор материальной точки
относительно S
- СО;
![]() ,
,
![]() - скорость и ускорение S
- СО относительно S
– СО в поступательном
движении;
- скорость и ускорение S
- СО относительно S
– СО в поступательном
движении;
![]() ,
,
![]() - угловая скорость и угловое ускорение
S
- СО относительно S
– СО во вращательном
движении. Тогда формула
пересчета скорости из движущейся S
- СО в «неподвижную» S
– СО имеет вид:
- угловая скорость и угловое ускорение
S
- СО относительно S
– СО во вращательном
движении. Тогда формула
пересчета скорости из движущейся S
- СО в «неподвижную» S
– СО имеет вид:
![]() ,
то есть, скорость материальной точки
относительно “неподвижной”
S – СО
складывается из скорости материальной
точки относительно движущейся S
- СО и скорости
,
то есть, скорость материальной точки
относительно “неподвижной”
S – СО
складывается из скорости материальной
точки относительно движущейся S
- СО и скорости
![]() точки S
- СО, через которую
проходит (в этот момент) материальная
точка, относительно S
– СО.
точки S
- СО, через которую
проходит (в этот момент) материальная
точка, относительно S
– СО.
Формула пересчета ускорения из движущейся s - со в «неподвижную» s - со
![]() тоже утверждает, что ускорение
материальной точки относительно
“неподвижной” S
– СО складывается из
ускорения материальной точки относительно
движущейся S
- СО и ускорения
тоже утверждает, что ускорение
материальной точки относительно
“неподвижной” S
– СО складывается из
ускорения материальной точки относительно
движущейся S
- СО и ускорения
![]() точки S
- СО, через которую
проходит (в этот момент) материальная
точка, относительно S
– СО. Кориолисово
ускорение
точки S
- СО, через которую
проходит (в этот момент) материальная
точка, относительно S
– СО. Кориолисово
ускорение
![]() .
Оно связано, во-первых,
с тем, что вектор
.
Оно связано, во-первых,
с тем, что вектор
![]() поворачивается вместе
с S
- СО и, во-вторых, с тем,
что из-за перемещения материальной
точки относительно S
- СО, изменяется
радиус-вектор
поворачивается вместе
с S
- СО и, во-вторых, с тем,
что из-за перемещения материальной
точки относительно S
- СО, изменяется
радиус-вектор
![]() ,
а значит и
скорость
,
а значит и
скорость
![]() .
.
СЕМИНАР 2 ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ И ПОСТУПАТЕЛЬНО ДВИЖУЩЕГОСЯ ТВЕРДОГО ТЕЛА
Инерциальные системы отсчета
Важная роль выбора системы отсчета впервые продемонстрирована Коперником (около 1500г.). В системе отсчета введенной Коперником, связанной с Солнцем и звездами, настолько упростился характер движения планет, что трудолюбивый Кеплер (в 1609-1619гг.) сумел сформулировать три знаменитых закона, описывающих движение планет. Следуя Копернику, Ньютон навсегда в качестве тел отсчета выбрал Солнце и звезды. Опираясь на законы Кеплера, Ньютон установил закон всемирного тяготения, а затем и три закона движения (около 1666г.). Все это было сделано применительно к коперниковой (гелиоцентрической), инерциальной системе отсчета.
Первый закон Ньютона содержит не только закон инерции Галилея, но и определение инерциальной системы отсчета:
Существуют такие системы отсчета, назовем их инерциальными (ИСО), в которых тело, изолированное от других тел, сохраняет свою скорость постоянной.
Нахождение силы из закона движения.
Импульсом материальной точки
называется величина, равная произведению
массы точки на ее скорость
![]() .
По определению, сила – это величина,
показывающая, как быстро изменяется
импульс материальной точки со временем,
то есть
.
По определению, сила – это величина,
показывающая, как быстро изменяется
импульс материальной точки со временем,
то есть
![]() ,
причем последние два равенства
справедливы, если масса тела постоянна.
,
причем последние два равенства
справедливы, если масса тела постоянна.
Интегрирование уравнения движения. Сила линейно зависит от времени.
![]() -
уравнение движения материальной точки
в векторной форме. В проекции на оси
прямоугольной системы координат
уравнения движения принимают вид
-
уравнение движения материальной точки
в векторной форме. В проекции на оси
прямоугольной системы координат
уравнения движения принимают вид
![]() ;
;
![]() ;
;
![]()
Интегрируем соответствующее дифференциальное уравнение методом разделения переменных.
Интегрирование уравнения движения. Сила зависит от координаты.
В уравнении движения
![]() делаем замену
делаем замену![]() .
Тогда уравнение принимает вид
.
Тогда уравнение принимает вид
![]() ,
то есть переменные разделились и можно
выполнить интегрирование.
,
то есть переменные разделились и можно
выполнить интегрирование.
Неинерциальные системы отсчета
Система отсчета, относительно которой материальная точка движется с ускорением, при условии, что на эту точку не действуют другие тела, называется неинерциальной (НСО).
Можно сказать иначе. Система отсчета, которая движется поступательно с ускорением и/или вращается относительно инерциальной системы отсчета (ИСО), называется неинерциальной (НСО).
Введем следующие обозначения:
![]() ,
,
![]() -
скорость и ускорение материальной точки
относительно неинерциальной
S
- СО;
-
скорость и ускорение материальной точки
относительно неинерциальной
S
- СО;
![]() - радиус-вектор материальной
точки относительно неинерциальной
S
- СО;
- радиус-вектор материальной
точки относительно неинерциальной
S
- СО;
![]() - ускорение неинерциальной
S
- СО относительно
инерциальной S
– СО в поступательном
движении;
- ускорение неинерциальной
S
- СО относительно
инерциальной S
– СО в поступательном
движении;
![]() ,
,
![]() - угловая скорость и угловое ускорение
неинерциальной S
- СО относительно
инерциальной S
– СО во вращательном
движении.
- угловая скорость и угловое ускорение
неинерциальной S
- СО относительно
инерциальной S
– СО во вращательном
движении.
В этих обозначениях уравнение
движения материальной точки в
неинерциальной системе отсчета имеет
вид:
![]() .
.
В правой части уравнения:
![]() - сумма
всех сил, действующих на материальную
точку со стороны других тел, то есть тех
сил, которые определены в рамках системы
законов Ньютона;
- сумма
всех сил, действующих на материальную
точку со стороны других тел, то есть тех
сил, которые определены в рамках системы
законов Ньютона;
![]() - сила
инерции, действующая в НСО, движущейся
поступательно с ускорением
- сила
инерции, действующая в НСО, движущейся
поступательно с ускорением
![]() ;
;
![]() - сила инерции, действующая
в НСО, вращающейся с угловым ускорением
- сила инерции, действующая
в НСО, вращающейся с угловым ускорением![]() ;
;
![]() - центробежная сила инерции,
действующая в НСО, вращающейся с угловой
скоростью
- центробежная сила инерции,
действующая в НСО, вращающейся с угловой
скоростью
![]() ;
;
![]() - сила инерции Кориолиса,
действующая в НСО, вращающейся с угловой
скоростью
- сила инерции Кориолиса,
действующая в НСО, вращающейся с угловой
скоростью
![]() ,
если материальная точка движется
относительно НСО со скоростью
,
если материальная точка движется
относительно НСО со скоростью![]() и при условии, что векторы
и при условии, что векторы
![]() и
и
![]() составляют угол, не равный 00
или 1800.
составляют угол, не равный 00
или 1800.
СЕМИНАР 3 ИМПУЛЬС, МЕХАНИЧЕСКАЯ ЭНЕРГИЯ И МОМЕНТ ИМПУЛЬСА (ЗАКОНЫ ИЗМЕНЕНИЯ И СОХРАНЕНИЯ)
Закон изменения импульса для одной материальной точки.
Второй закон Ньютона для
материальной точки, когда на нее действует
постоянная сила, может быть переписан
в виде закона изменения импульса
![]() - приращение импульса материальной
точки равно импульсу силы (произведению
силы на время, за которое импульс точки
изменился на
- приращение импульса материальной
точки равно импульсу силы (произведению
силы на время, за которое импульс точки
изменился на![]() ),
действующей на материальную точку.
),
действующей на материальную точку.
Система материальных точек.
Импульс системы материальных
точек – это сумма (конечно векторная)
импульсов материальных точек:
![]() .
Производная импульса системы материальных
точек по времени равна сумме всех сил,
действующих на систему, и, с учетом
третьего закона Ньютона, равна сумме
внешних сил, действующих на систему
материальных точек:
.
Производная импульса системы материальных
точек по времени равна сумме всех сил,
действующих на систему, и, с учетом
третьего закона Ньютона, равна сумме
внешних сил, действующих на систему
материальных точек:
![]() .
.
Сохранение импульса системы взаимодействующих тел.
Из закона изменения импульса
![]() следует, что если
следует, что если
![]() ,
то
,
то![]() .
Для проекций на выделенное направление
X можно утверждать,
что из
.
Для проекций на выделенное направление
X можно утверждать,
что из
![]() следует
следует
![]() ,
если
,
если
![]() .
.
Уравнение движения тела с
изменяющееся массой – уравнение
Мещерского
![]() Здесь m – масса,
Здесь m – масса,
![]() - ускорение тела в рассматриваемый
момент времени,
- ускорение тела в рассматриваемый
момент времени,
![]() - сумма всех внешних сил,
- сумма всех внешних сил,
![]() - реактивная сила.
- реактивная сила.
Центр масс. Система отсчета центра масс.
Центром масс системы
материальных точек называется точка
пространства, радиус-вектор которой
находится по формуле
![]() .
Соответственно скорость центра масс
равна
.
Соответственно скорость центра масс
равна
![]() .
Системой отсчета центра масс (Ц-системой)
называется такая система отсчета,
относительно которой покоится центр
масс рассматриваемой системы частиц,
и, которая движется поступательно
относительно инерциальной системы
отсчета.
.
Системой отсчета центра масс (Ц-системой)
называется такая система отсчета,
относительно которой покоится центр
масс рассматриваемой системы частиц,
и, которая движется поступательно
относительно инерциальной системы
отсчета.
Работа постоянной силы.
![]() - работа постоянной силы,
приложенной к телу, определяется как
скалярное произведение вектора силы
на вектор перемещения тела.
- работа постоянной силы,
приложенной к телу, определяется как
скалярное произведение вектора силы
на вектор перемещения тела.
Работа переменной силы.
Разделяем конечное перемещение
![]() на такие элементарные перемещения
на такие элементарные перемещения![]() ,
чтобы на любом из них можно было считать
силу постоянной по величине и по
направлению. Тогда можно ввести понятие
элементарной работы
,
чтобы на любом из них можно было считать
силу постоянной по величине и по
направлению. Тогда можно ввести понятие
элементарной работы
![]() .
Затем учитываем замечательное свойство
работы - аддитивность (свойство
складываться):
.
Затем учитываем замечательное свойство
работы - аддитивность (свойство
складываться):
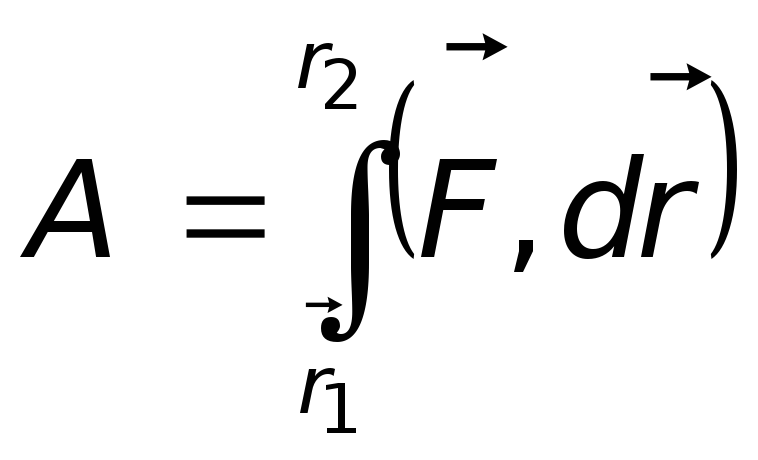 .
.
Мощность силы
![]() .
.
Теорема о приращении
кинетической энергии.
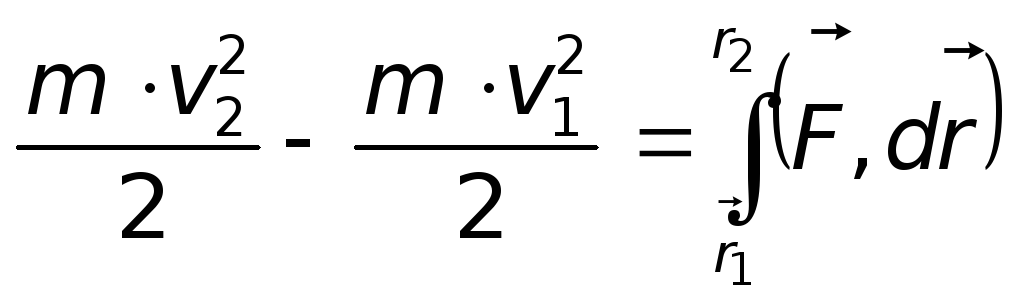 -
приращение кинетической энергии
материальной точки или поступательно
движущегося твердого тела равно работе
всех сил, приложенных к материальной
точке или к телу.
-
приращение кинетической энергии
материальной точки или поступательно
движущегося твердого тела равно работе
всех сил, приложенных к материальной
точке или к телу.
Потенциальная энергия взаимодействия системы материальных точек.
Для того, чтобы работа силы,
приложенной к телу, при переносе тела
из позиции 1 в позицию 2
 не зависела от формы траектории,
необходимо, чтобы сумма
не зависела от формы траектории,
необходимо, чтобы сумма![]()
![]() была полным дифференциалом. В свою
очередь, для того, чтобы указанная сумма
была полным дифференциалом, должны
выполняться равенства
была полным дифференциалом. В свою
очередь, для того, чтобы указанная сумма
была полным дифференциалом, должны
выполняться равенства
![]() ;
;
![]() ;
;
![]() .
Только при выполнении этих условий
можно сопоставить точкам пространства
.
Только при выполнении этих условий
можно сопоставить точкам пространства
![]() некоторую функцию координат
некоторую функцию координат
![]() и назвать ее потенциальной энергией, а
силу потенциальной или консервативной.
Определение формулируется не для
потенциальной энергии, а для ее приращения
и назвать ее потенциальной энергией, а
силу потенциальной или консервативной.
Определение формулируется не для
потенциальной энергии, а для ее приращения
 ,
или ее убыли
,
или ее убыли
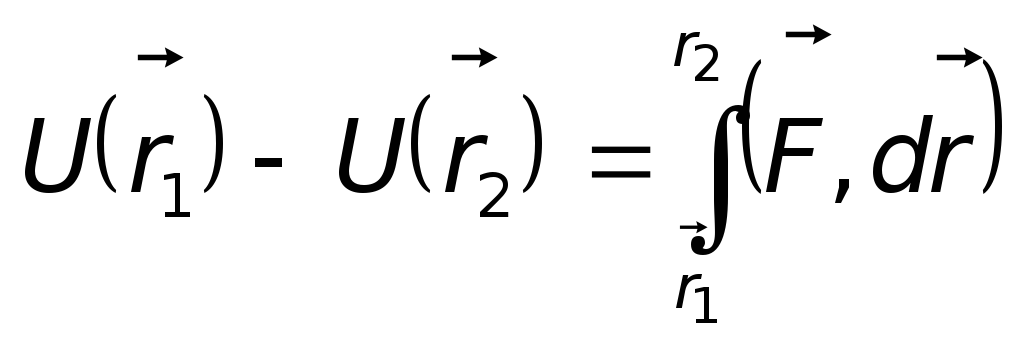 .
.
Таким образом, потенциальная
энергия неопределенна с точностью до
постоянной – уровня отсчета потенциальной
энергии. Определение приращения
потенциальной энергии в дифференциальной
форме имеет вид
![]() .
Отсюда
.
Отсюда
![]() .
.
