1 семестр МП / Лабы / Приложение к LAB 8,9

Ф

Z

r

изические основы

с

M

помощью

1. Т

   

   

   

   A

   D

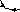   рифилярный подвес до (штрихпунктирные линии) и после «закручивания» (сплошные линии) на угол

O

B

C

R

M

2. Вектор силы натяжения нити    в пространстве

,

е

A

O

D

сли ускорение поступательного движения нижнего диска ,

C

B

( – масса нижнего диска)

A

D

O

3. П

   B

   

   роекция силы натяжения нити в плоскости нижнего диска

C

измерения момента инерции

трифилярного подвеса

Угол и угол опираются на одну и ту же дугу , поэтому для малых углов

,                                           (1)

соответственно

                                            (2)

Проекция силы натяжения нити, обеспечивающая крутильные колебания нижнего диска , равна:

                                     (3)

Соответствующий суммарный момент сил для трех нитей можно вычислить как:

                              (4)

Запишем основное уравнение динамики вращательного движения нижнего диска:

,                               (5)

где – момент инерции диска.

Преобразуем (5) к уравнению колебаний

                             (6)

Тогда период колебаний равен

                           (7)

Таким образом, экспериментально определив период , можно рассчитать момент инерции :

                           (8)