Лекция 1

Глава 1. Множества, бинарные отношения, комбинаторика

§ 1.1. Множества и бинарные отношения

Множество, способы задания множеств. Мощность конечного множества. Подмножество. Операции над множествами: дополнение, объединение, пересечение, разность, декартово произведение. Правило суммы, формула включений и исключений. Бинарное отношение на множестве. Свойства бинарных отношений: рефлексивность, симметричность, транзитивность. Отношение эквивалентности и отношение порядка.

Базовые понятия и утверждения

1. Множества и операции над ними. Под множеством понимают объединение в единое целое определенных вполне различаемых объектов. Объекты при этом называют элементами образуемого ими множества.

Для обозначения множеств используют прописные буквы, а для обозначения элементов множеств - строчные буквы латинского алфавита.

Запись означает, что является элементом множества ; в противном случае пишут .

Множество называют конечным, если оно содержит конечное число элементов, и бесконечным, если оно содержит бесконечное число элементов. Множество, не содержащее элементов, называют пустым и обозначают символом .

Число элементов конечного множества называют его мощностью и обозначают .

Множество можно описать, указав свойство, присущее элементам только этого множества. Множество всех объектов, обладающих свойством , обозначают . Конечное множество можно задать путем перечисления его элементов, т.е. .

Например, запись означает, что множество содержит два элемента - числа и .

Если каждый элемент множества есть элемент множества B , то говорят, что есть подмножество , и пишут: .

Заметим, что пустое множество считают подмножеством любого множества.

Если и , то говорят, что множества и равны, и пишут: .

Если и , то называют собственным подмножеством и, чтобы подчеркнуть это, применяют запись .

Множество всех подмножеств множества называют его булеаном и обозначают .

Например, если , то

.

Вводят целый ряд операций над множествами, позволяющих получать из одних множеств другие.

1. Множество, состоящее из тех и только тех элементов, которые принадлежат хотя бы одному из множеств и , называют объединением A и B и обозначают , т.е. .

2. Множество, состоящее из тех и только тех элементов, которые принадлежат как множеству , так и множеству , называют пересечением A и B и обозначают , т.е. .

Если , то множества и называют непересекающимися.

3. Множество, состоящее из всех элементов множества , не принадлежащих множеству , называют разностью A и B и обозначают , т.е. .

4. Обычно в конкретных рассуждениях всякое множество рассматривают как подмножество некоторого достаточно широкого множества, которое называют универсальным. Множество элементов универсального множества , не принадлежащих множеству , называют дополнением и обозначают , т.е. . Из определения следует, что .

5. Множество, состоящее из упорядоченных пар , в которых - элемент множества , а - элемент множества , называют декартовым произведением множеств A и B и обозначают , т.е. .

Удобным приемом наглядного изображения операций являются диаграммы Эйлера - Венна. На них множества представлены плоскими фигурами (чаще всего кругами). Области, соответствующие множествам, полученным в результате операции, обычно выделяют цветом. На рис. 1.1 приведены диаграммы Эйлера - Венна, иллюстрирующие некоторые из введенных операций.

Рис. 1.1.

В качестве примера найдем объединение, пересечение, разность и декартово произведение множеств и .

Поскольку , , то , , , .

Пусть задано универсальное множество . Тогда для любых множеств выполняются следующие свойства:

коммутативные законы:

1. ; 2. ;

ассоциативные законы:

3.;

4. ;

дистрибутивные законы:

5.;

6. ;

законы идемпотентности:

7. ; 8. ;

законы де Моргана:

9. ; 10. ;

законы нуля:

11. ; 12. ;

законы единицы:

13. ; 14. ;

законы поглощения:

15. ; 16. ;

законы дополнения:

17. ; 18. ;

закон двойного дополнения:

19. .

О том, как доказываются эти равенства, можно узнать во второй части данного параграфа.

Операции объединения, пересечения и декартова произведения можно обобщить на случай произвольного конечного числа участников.

Объединением множеств называют множество, любой элемент которого является элементом хотя бы одного из данных множеств. Обозначение: или .

Пересечением множеств называют множество, любой элемент которого является элементом каждого из данных множеств. Обозначение: или .

Декартовым произведением множеств называют множество

.

В частном случае одинаковых сомножителей декартово произведение обозначают .

Например, если , то

,

.

Приведем без доказательств утверждения о числе элементов конечных множеств.

1. Если между конечными множествами и существует взаимно-однозначное соответствие, то .

2. Если - конечные множества, то множество также конечно и

.

Например, если , то множество имеет мощность .

3. Если - конечные попарно-непересекающиеся множества, то множество также конечно и

.

Это утверждение называют правилом суммы.

4. Если - конечные множества, то множество также конечно и

.

Последнее равенство называется формулой включений и исключений. В частных случаях двух и трех множеств она принимает вид:

;

.

Заметим, что формула включений и исключений действует и в том случае, когда множества попарно не пересекаются (в этом случае все слагаемые в правой части формулы, содержащие пересечения множеств, обнуляются и формула трансформируется в правило суммы).

Пусть, например, , , , причем , а . Тогда можно найти по правилу суммы: , а для поиска нужно использовать формулу включений и исключений: .

Пример 1. В группе из 100 туристов 65 человек знают английский язык, 55 человек знают французский и 38 человек знают оба языка. Сколько туристов в группе знает хотя бы один из этих языков?

◄ Пусть и - множества туристов, знающих соответственно английский и французский язык. Тогда - множество туристов, знающих хотя бы один из этих языков. Число таких туристов находим по формуле включений и исключений . ►

Совокупность непустых, попарно непересекающихся подмножеств множества называют разбиением , если .

Например, для множества совокупность подмножеств разбиением является, а совокупность подмножеств не является.

2. Бинарные отношения на множестве. Бинарные отношения -простой и вместе с тем очень важный объект дискретной математики.

Определение. Бинарным отношением на множестве называется подмножество декартова произведения .

Для обозначения бинарных отношений, как правило, будем использовать строчные буквы греческого алфавита: и т.п.

Пусть - некоторое бинарное отношение на множестве . Если , то говорят, что и связаны бинарным отношением и пишут .

Пример 2. Пусть . Тогда

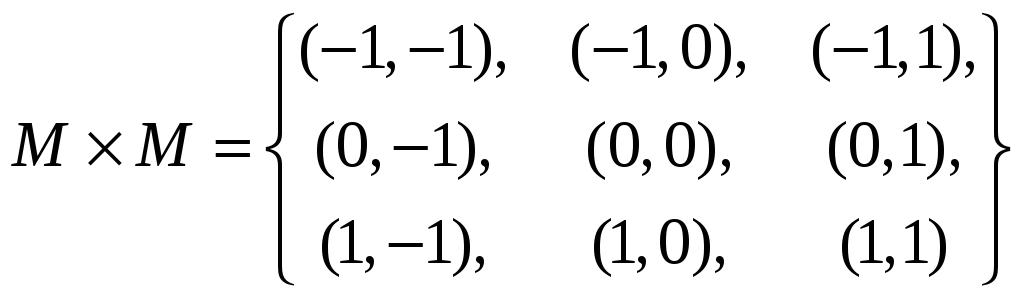
и следующие множества могут служить примерами бинарных отношений на множестве :

;

;

;

.

Перечислим ряд важных свойств, которыми могут обладать бинарные отношения.

Определенное на множестве бинарное отношение :

рефлексивно, если для выполняется ;

симметрично, если для из следует ;

антисимметрично, если для из и следует ;

транзитивно, если для из и следует .

Определение. Если бинарное отношение рефлексивно, симметрично и транзитивно одновременно, то оно называется отношением эквивалентности.

Например, бинарное отношение из примера 2 рефлексивно, антисимметрично и транзитивно, - антисимметрично и транзитивно, - рефлексивно, симметрично, антисимметрично и транзитивно, - рефлексивно, симметрично и транзитивно. Следовательно, бинарные отношения и являются отношениями эквивалентности, а и - нет.

Определение. Пусть - отношение эквивалентности на множестве и - элемент . Классом эквивалентности элемента по бинарному отношению называют множество .

Например, множества , , - классы эквивалентности элементов по отношению , а , , - классы эквивалентности элементов по .

Перечислим свойства классов эквивалентности, присущие любому отношению эквивалентности, определенному на произвольном множестве .

1. Класс эквивалентности любого элемента множества - непустое множество.

2. Классы эквивалентности любых двух элементов множества либо не пересекаются, либо совпадают.

3. Объединение классов эквивалентности всех элементов множества совпадает с самим множеством .

Доказательство этих свойств приведено во второй части параграфа.

Из свойств классов эквивалентности следует утверждение: всякое отношение эквивалентности, заданное на множестве , порождает разбиение множества на классы эквивалентности этого отношения.

Для иллюстрации этого утверждения вновь обратимся к бинарным отношениям и из примера 2.

Очевидно, что классы эквивалентности , , элементов множества по отношению не пусты, попарно не пересекаются, а их объединение совпадает с самим множеством . Следовательно, порождает разбиение множества на три подмножества: , , .

Для классов эквивалентности , , элементов по отношению имеем: классы эквивалентности элементов и совпадают и при этом не имеют общих элементов с классом эквивалентности элемента , объединение всех классов совпадает с множеством . Следовательно, отношение порождает разбиение множества на два подмножества: , .

Рассмотрим еще один важный класс бинарных отношений.

Определение. Бинарное отношение называется отношением порядка, если оно рефлексивно, антисимметрично и транзитивно.

Пусть - отношение порядка на . Если для любых двух элементов и множества верно, что либо , либо , то называют отношением линейного порядка. В противном случае говорят, что - отношение частичного порядка.

Например, отношениями порядка являются отношения и из примера 2 ( - линейного, - частичного).

Пример 3. Рассмотрим на множестве бинарное отношение , определяемое условием . Это отношение рефлексивно, антисимметрично и транзитивно, и, значит, является отношением порядка, причем частичного, поскольку элемент не связан с элементом и элемент не связан с элементом .