Изометрия

Рассмотрим наиболее широко применяемую аксонометрическую проекцию – прямоугольную изометрию.

Изометрию любого предмета начинают строить с нанесения аксонометрических осей.

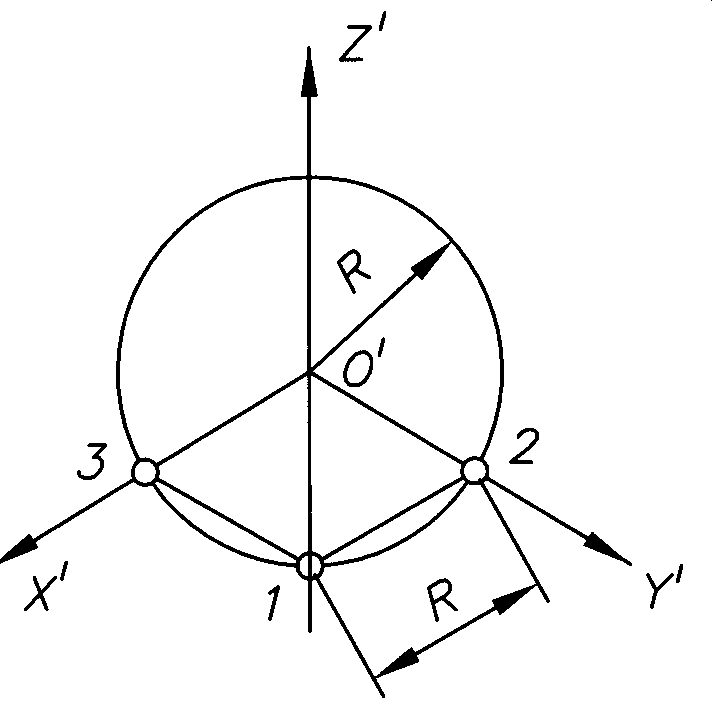
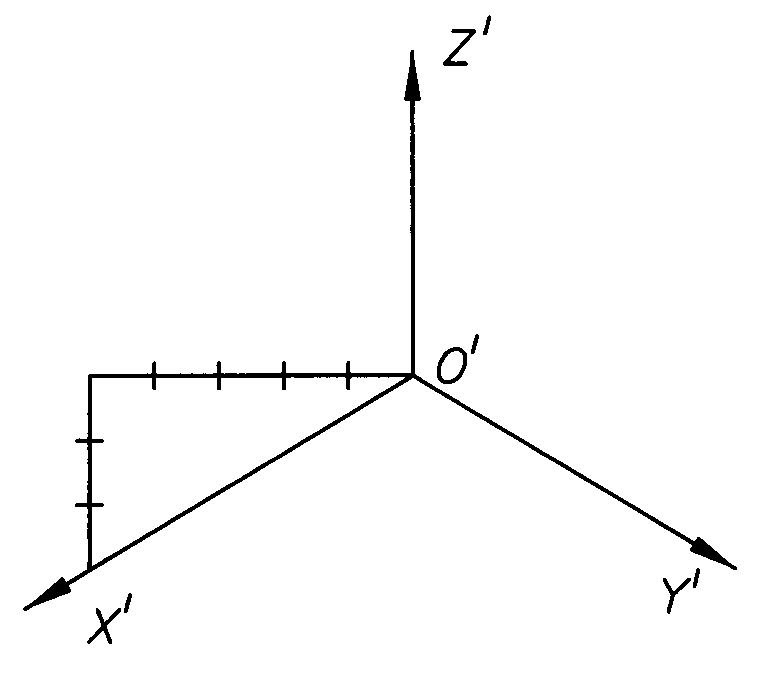
Графическое построение осей, расположенных под 120 относительно друг к другу:

1. Если используется бумага в клетку, то оси строятся, как показано на рис.4.3,а.

а б в

Рис.4.3.

2. При наличии транспортира оси строят по рис.4.3,б, отложив при построении осейX иYпо 30от горизонтальной линии.

3. С помощью циркуля оси строят по рис.4.3,в: на осиZв любом удобном месте берут центр окружностиО; произвольным радиусом проводят окружность; из точки1(пересечения окружности с осьюZ) значением радиуса окружности делают засечки на окружности влево и вправо; через полученные точки2и3и центр окружностиО проводят осиXиY.

Построение аксонометрической проекции точки

Вортогональных проекциях точка задана на рис.4.4,а.

А б

Рис.4.4.

Порядок построения аксонометрической проекции точки (рис.4.4,б):

• в произвольном масштабе на оси Xоткладывают координатуx _A;

• параллельно оси Y– координатуy_Aи получают вторичную проекциюА₁;

• из точки А₁откладывают координатуz_А, параллельно осиZи получают аксонометрическую проекциюА точкиА.

Построение аксонометрических проекций окружностей

При построении окружностей в аксонометрических плоскостях П₁,П₂,П₃следует помнить:

• изометрическая проекция окружности представляет собой эллипс;

• эллипсы, изображающие изометрические проекции окружностей в плоскостях П₁,П₂,П₃одинаковы (рис.4.5);

Рис.4.5.

• большая ось эллипса всегда направлена перпендикулярно отсутствующей в заданной плоскости оси;

• в практике черчения эллипсы заменяют овалами. Рекомендуется овал строить с помощью ромба, стороны которого параллельны осям плоскости проекции, в которой расположена заданная окружность (порядок построения см. ниже);

• большая и малая оси эллипса располагаются по диагоналям ромба.

Построение изометрии предмета по ортогональным проекциям

Построение изометрии предмета по ортогональным проекциям показано на рис.4.6. На рис.4.6,а представлены ортогональные проекции предмета. Окружность заключена в квадрат, а весь предмет – в габаритный параллелепипед.

Порядок построения:

• задавшись точкой О, строят проекции описанного квадрата, т.е. ромб (рис.4.6,б), начиная с точек1и2, лежащих на осяхXиZ и проводя стороны ромба через точку3параллельно осямXиZ ;

а б

Рис.4.6.

в г

Рис.4.6.

• проводят большую диагональ ромба;

• проекцию полуокружности – эллипс – заменяют овалом; проводят дугу из центра Ц₁;

• соединив Ц₁с верхней точкой эллипса (точкой 2) на осиZ, получают на диагонали точкуЦ₂ – центр второй дуги овала;

• достраивают передний фронтальный контур предмета по координатам точек, перенося их с ортогональных проекций;

• для построения заднего контура предмета, прежде всего полуовала, откладывают из центров Ц₁иЦ₂ по (параллельно) осиYтолщинуа, взятую с горизонтальной проекции (рис.4.6,а), и получают центрыЦ₁иЦ₂для дуг заднего контура;

• огибающую для проекции цилиндра проводят касательно к обеим дугам;

• аналогично ромбу (проекции описывающего окружность квадрата) строят отверстие (рис.4.6,в);

• разрез выполняют плоскостями проходящими через оси XиZ(рис.4.6,г); контур участков разреза ограничен осямиX иY,YиZ, а также параллельными им отрезками;

а б

Рис.4.7.

• штриховку наносят по направлению больших диагоналей ромба в каждой аксонометрической плоскости проекций (рис.4.7,а) или перпендикулярно им (рис.4.7,б);

• ребра (тонкие стенки), попадающие в продольный разрез, штрихуют.