Реферат / 28. Линии напряжённости электростатического поля. Поток вектора напряжённости. Теорема Отсроградского-Гаусса

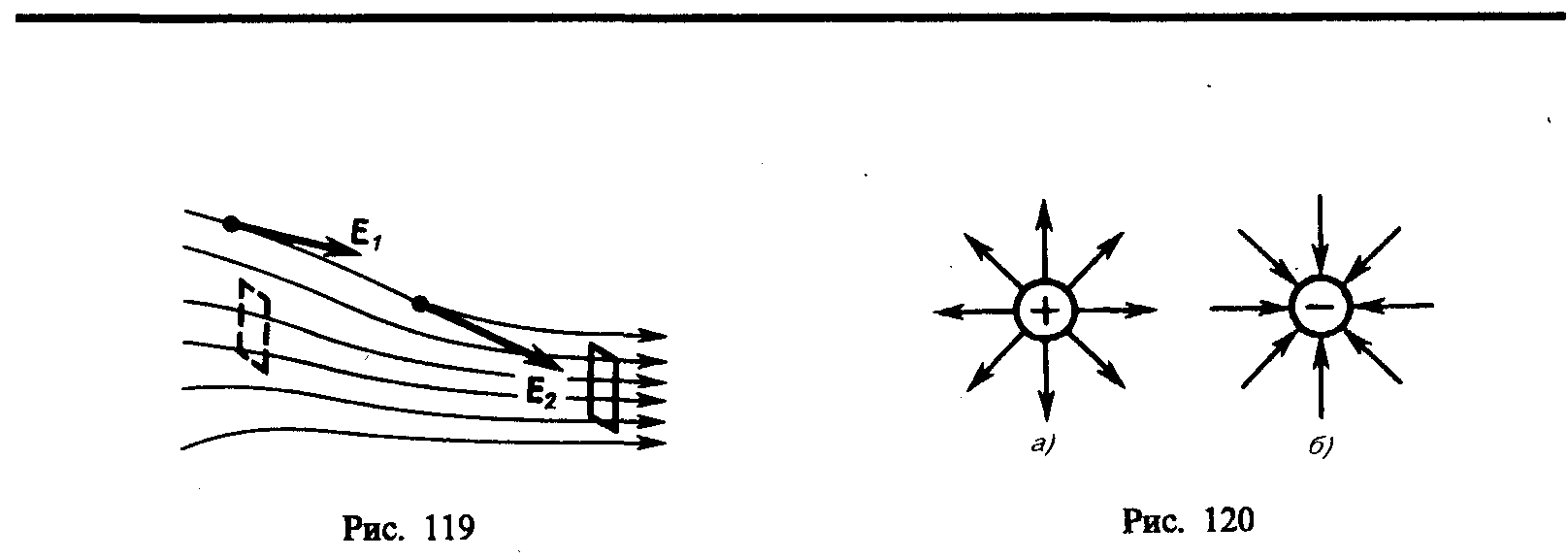
Графически электростатическое поле изображают с помощью линий напряженности — линий, касательные к которым в каждой точке совпадают с направлением вектора Е (рис. 119). Линиям напряженности приписывается направление, совпадающее с направлением вектора напряженности. Так как в каждой данной точке пространства вектор напряженности имеет лишь одно направление, то линии напряженности никогда не пересекаются. Для однородного поля (когда вектор напряженности в любой точке постоянен по величине и направлению) линии напряженности параллельны вектору напряженности. Если поле создается точечным зарядом, то линии напряженности — радиальные прямые, выходящие из заряда, если он положителен (рис. 120, а), и входя­щие в него, если заряд отрицателен (рис. 120, б). Вследствие большой наглядности графический способ представления электростатического поля широко применяется в электротехнике.

Чтобы с помощью линий напряженности можно было характеризовать не только направление, но и значение напряженности электростатического поля, условились про­водить их с определенной густотой (см. рис. 119): число линий напряженности, прони­зывающих единицу площади поверхности, перпендикулярную линиям напряженности, должно быть равно модулю вектора Е. Тогда число линий напряженности, пронизыва­ющих элементарную площадку dS, нормаль n которой образует угол  с вектором Е, равно Е dS cos = E_ndS, где Е_п—проекция вектора Е на нормаль n к площадке dS (рис. 121).Величина

называется потоком вектора напряженности через площадку dS. Здесь dS = dSn — век­тор, модуль которого равен dS, а направление совпадает с направлением нормали n к площадке. Выбор направления вектора n (а следовательно, и dS) условен, так как его можно направить в любую сторону. Единица потока вектора напряженности электростатического поля — 1 Вм.

Для произвольной замкнутой поверхности S поток вектора Е сквозь эту поверх­ность

(79.3)

где интеграл берется по замкнутой поверхности S. Поток вектора Е является алгебра­ической величиной: зависит не только от конфигурации поля Е, но и от выбора направления n. Для замкнутых поверхностей за положительное направление нормали принимается внешняя нормаль, т. е. нормаль, направленная наружу области, охватыва­емой поверхностью.

Теорема Остроградского-Гаусса.

1) поле созда­но изолированным положительным точечным зарядом q и что поверх­ностью является сфера радиуса r, в центре которой расположен точечный заряд (Риc. 6). Чему равен поток Ф через такую поверхность?

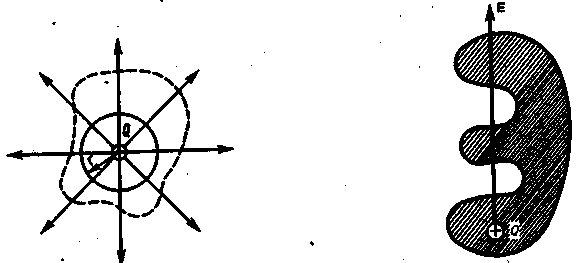
в каждой точке поверхности

`E = (1/4pe<sub>0</sub>)(q/r<sup>3</sup>)`r, а поверхность сферы S=4pr², тогда

Ф = E×4pr²= (q/4pe₀ r²) 4pr²=q/e₀.

поток не зависит от размеров сфе­ры.

2).поток не зависит и от формы поверхности,окружающей заряд q. Проведем две концентрические сферы разных радиусов. Мы увидим, что число линий напряженности электрического поля, пронизывающих сферы, одинаково. Между этими сферами линии вектора напряженности `Е идут непрерывно, нигде не заканчиваясь и не начинаясь вновь. Поэтому, если мы проведем между этими сферами замкнутую поверхность S₁ произвольной формы, тоже охватывающую заряд q, то поток вектора напряженности через эту поверхность также будет равен q/e₀.

линии напряженности электрического поля начинаются и заканчиваются только на электрических зарядах. Если замкнутая поверх­ность не охватывает заряда, то поток вектора электрического поля через эту поверхность равен нулю, т.к. число силовых линий, входящих в поверхность, рав­но числу выходящих из неё.

3). Пусть поле создается не одним точечным зарядом, а произволь­ной системой точечных зарядов q₁, q₂, q_3…q_n. По принципу суперпозиции на­пряжённость результирующего электростатического поля равна векторной сумме напряжённостей электростатических полей, создаваемых каждым из зарядов в отдельности :

E = `E<sub>1</sub>+`E₂ +`E<sub>3</sub> +…+`E_n = S`E_i.

поэтому проекция вектора `Е на на­правление нормали к площади dS равна алгебраической сумме проекций всех векторов `Е_i на это направление

Поток напряженности результирующего поля сквозь произвольную замкнутую поверхность S, охватывающую заряды q₁, q₂, …q_k , и не охватывающую заряды q_k+1…q_m, равен , но Ф_i=0, если i>k поэтому ,т.е.поток вектора напряженности электростатического поля в вакууме сквозь произвольную замкнутую поверхность равен отношению алгебраической суммы зарядов, охватываемых этой поверхностью, к электрической постоянной. Это и есть теорема Оетроградского -Гаусса применительно к электростатическому полю в вакууме. Теорема Остроградского-Гаусса выведена нами как прямое следствие из закона Кулона. Она позволяет сравнительно просто рассчитывать электрические поля при симмет­ричных распределениях зарядов и окружающих их диэлектриков.