
- •7. Дифракция Френеля на круглом отверстии.
- •6.2 Дифракция Френеля на круглом экране.
- •8. Дифракция Фраунгофера на одной щели
- •9. Дифракционная решетка. Дифракционный спектр
- •14. Поляризация при отражении и преломлении. Закон Брюстера
- •15. Двойное лучепреломление
- •17. Вращение плоскости поляризации. Определение концентрации оптически активных веществ.
- •16. Искусственное двойное лучепреломление.
- •12.1 Естественный и поляризованный свет.
- •Закон Малюса
- •11. Дифракция рентгеновских лучей на кристаллической решетке. Исследования структуры кристаллов
- •10. Дисперсия и разрешающая способность решётки.
- •2. Когерентные волны. Интерференция света. Оптическая разность хода
- •3. Интерференция света от двух когерентных источников
- •1. Световые волны
- •Шкала электромагнитного излучения
- •25. Земная атмосфера и солнечная радиация
- •18.1. Тепловое излучение
- •19.1. Абсолютно черное тело
- •18.2. Закон Кирхгофа
- •19.2. Закон Стефана-Больцмана
- •20.1. Закон смещения Вина.
- •20.2. Формула Релея-Джинса
- •21. Квантовая гипотеза и формула Планка
- •22. Оптическая пирометрия
- •23.1. Фотоэффект
- •23.2. Законы внешнего фотоэффекта
- •23.3. Уравнение Эйнштейна
- •27. Постулаты Бора
- •28. Гипотеза де Бройля
- •26.2. Модели атома Томсона и Резерфорда
- •24. Поглощение света веществом
7. Дифракция Френеля на круглом отверстии.
Сферическая волна, распространяющаяся из точечного источника S, встречает на своем пути экран с круглым отверстием. Дифракционную картину наблюдаем на экране (Э) в точке В, лежащей на линии, соединяющей S с центром отверстия (рис. 258). Экран параллелен плоскости отверстия и находится от него на расстоянии b. Вид дифракционной картины зависит от числа зон Френеля, укладывающихся в отверстии. Для точки В, согласно методу зон Френеля (см. (178.1) и (178.6)), амплитуда результирующего колебания
![]() где
знак плюс соответствует нечетным т
и минус —
четным т.
где
знак плюс соответствует нечетным т
и минус —
четным т.
Когда отверстие открывает нечетное число зон Френеля, то амплитуда (интенсивность) в точке В будет больше, чем при свободном распространении волны, если четное, то амплитуда (интенсивность) будет равна нулю. Если в отверстии укладывается две зоны Френеля, то их действия в точке В практически уничтожат друг друга из-за интерференции. Таким образом, дифракционная картина от круглого отверстия вблизи точки В будет иметь вид чередующихся темных и светлых колец с центрами в точке В (если т четное, то в центре будет темное кольцо, если m нечетное — светлое кольцо), причем интенсивность максимумов убывает с расстоянием от центра картины.
Расчет амплитуды результирующего колебания на внеосевых участках экрана более сложен, так как соответствующие им зоны Френеля частично перекрываются непрозрачным экраном. Если отверстие освещается не монохроматическим, а белым светом, то кольца окрашены.


6.2 Дифракция Френеля на круглом экране.
Сферическая волна, распространяющаяся от точечного источника S, встречает на своем пути диск. Дифракционную картину наблюдаем на экране (Э) в точке В, лежащей на линии, соединяющей S с центром диска (рис. 259). В данном случае закрытый диском участок фронта волны надо исключить из рассмотрения и зоны Френеля строить начиная с краев диска. Пусть диск закрывает т первых зон Френеля. Тогда амплитуда результирующего колебания в точке В равна
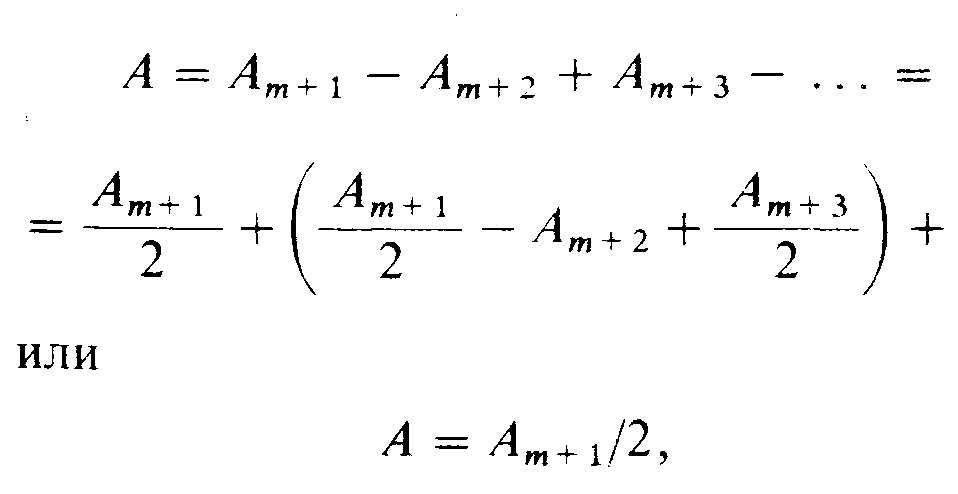
так как выражения, стоящие в скобках, равны нулю. Следовательно, в точке В всегда наблюдается интерференционный максимум (светлое пятно), соответству-ющий половине действия первой открытой зоны Френеля. Центральный максимум окружен концентрическими с ним темными и светлыми кольцами, а интенсивность максимумов убывает с расстоянием от центра картины.
8. Дифракция Фраунгофера на одной щели
Немецкий физик И. Фраунгофер рассмотрел дифракцию плоских световых волн, или дифракцию в параллельных лучах. Дифракция Фраунгофера, имеющая большое практическое значение, наблюдается в том случае, когда источник света и точка наблюдения бесконечно удалены от препятствия, вызвавшего дифракцию. Чтобы этот тип дифракции осуществить, достаточно источник света поместить в фокусе собирающей линзы, а дифракционную картину исследовать в фокальной плоскости второй собирающей линзы, установленной за препятствием.
Рассмотрим дифракцию Фраунгофера от бесконечно длинной щели (для этого практически достаточно, чтобы длина щели была значительно больше ее ширины). Пусть плоская монохроматическая световая волна падает нормально плоскости щели шириной а (рис. 260, а).
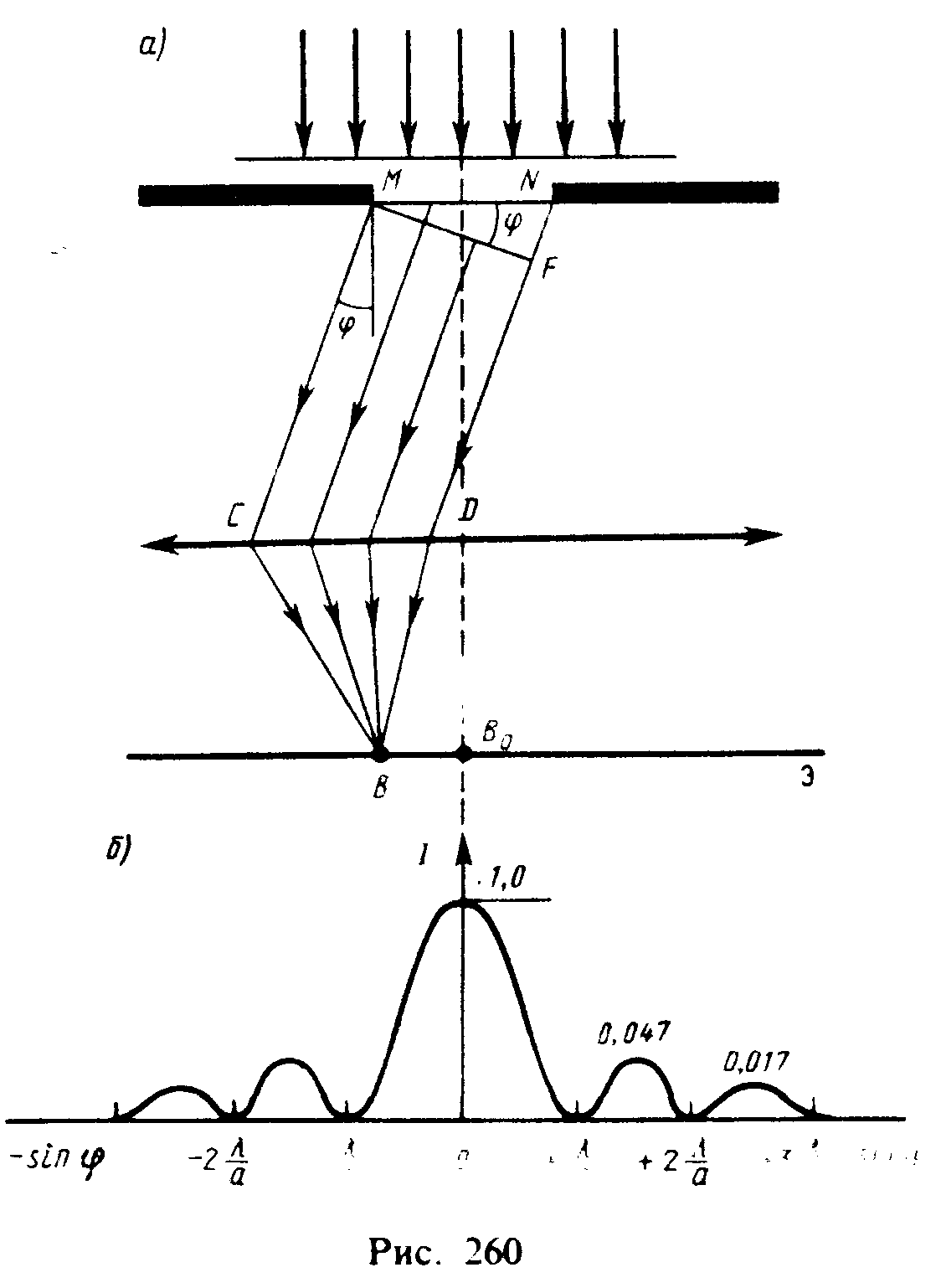
Оптическая разность хода между крайними лучами МС и ND, идущими от щели в произвольном направлении фи,
![]() где
F
— основание
перпендикуляра, опущенного
из точки М на
луч ND.
где
F
— основание
перпендикуляра, опущенного
из точки М на
луч ND.
Из выражения (180.1) вытекает, что число зон Френеля, укладывающихся на ширине щели, зависит от угла фи. От числа зон Френеля, в свою очередь, зависит результат наложения всех вторичных волн. Из приведенного построения следует, что при интерференции света от каждой пары соседних зон Френеля амплитуда результирующих колебаний равна нулю, так как колебания от каждой пары соседних зон взаимно погашают друг друга. Следовательно, если число зон Френеля четное
![]()
то в точке В наблюдается дифракционный минимум (полная темнота), если же число зон Френеля нечетное
![]()
то наблюдается дифракционный максимум, соответствующий действию одной нескомпенсированной зоны Френеля. Отметим, что в прямом направлении (фи = 0) щель действует как одна зона Френеля и в этом направлении свет распространяется с наибольшей интенсивностью, т. е. в точке В0 наблюдается центральный дифракционный максимум.
