9. ПОБУДОВА ПОВЕРХОНЬ ЗА ДОПОМОГОЮ ІНТЕРПОЛЯЦІЇ

Як це не парадоксально звучить, усі точні науки перейняті ідеєю апроксимації.

Б. Рассел

В основі методів моделювання (побудови) безперервних поверхонь на основі дискретних (точкових) масивів просторово-координованих даних лежать процедури просторової інтерполяції. При цьому використовуються як стохастичні, так і детерміновані дані.

На сьогодні існує багато методів, що дозволяють розв’язувати цю задачу. Серед них – інтерполяція на основі триангуляції Делоне, метод зворотно зважених відстаней, метод природної околиці, методи сплайнапроксимації, трендів, радіальних базисних функцій, крігінг та багато інших.

9.1. Загальні відомості про апроксимацію та інтерполяцію

Створення поверхні в ГІС – заповнення простору між наявними дискретними точками, що містять дані вимірів певного безперервного явища.

Стандартним засобом такого моделювання є інтерполяція. Наприклад, дані отримані з невпорядковано розташованих метеорологічних станцій у регіоні, можуть бути використані для створення растрових поверхонь температури, атмосферного тиску, вологості, забруднення повітря тощо. При цьому використовуються як стохастичні, так і детерміністичні підходи.

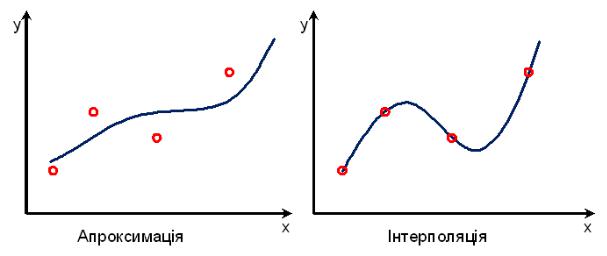
Відмінності між інтерполяцією та апроксимацією представлені на рис. 9.1.

Рис. 9.1. Відмінності апроксимації та інтерполяції

181

Процес апроксимації полягає в побудові наближеної (апроксимуючої) функції, що проходить через всі точки вихідних даних і найближче до заданої неперервної функції. Підбір емпіричної функції здійснюється вибором з усіх функцій на основі обчислених параметрів, що входять в ці функції, найбільш близько описують функціональну залежність між досліджуваними величинами.

Інтерполяція – процес отримання значень певної властивості в точках, розташованих поміж точками вимірів, тобто призначення інтер-

поляції в ГІС полягає в тому, щоб заповнити проміжки між відомими точками вимірів і таким чином змоделювати безперервний розподіл властивості (атрибуту).

Інтерполяція будується на припущенні, що просторово розподілені об’єкти корелюються в просторі, тобто об’єкти, розташовані поруч, мають схожі характеристики. Наприклад, якщо йде сніг на одній стороні вулиці, можна з великою ймовірністю стверджувати, що сніг іде і на іншій стороні вулиці. Менш імовірно, що сніг іде на території всього міста, і ще менш імовірно, що опади відбуваються на всій території області, регіону, країни тощо.

Просторова інтерполяція точкових даних ґрунтується на виборі аналітичної моделі поверхні. Процедура переходу від значень у дискретних точках до поверхні є нетривіальною і неоднозначною; для різноманітних задач і типів даних потрібні різні алгоритми (вірніше, не "потрібні", а "краще підходять", оскільки на 100 %, придатних не існує). Саме тому для створення поверхонь пропонуються різні методи створення поверхонь за точковими даними. Кожний з цих методів інтерполяції припускає різні шляхи отримання значень. Ефективність програми інтерполяції визначається:

–набором методів інтерполяції;

–можливістю дослідника керувати параметрами методів інтерполяції;

–наявністю засобів оцінки точності і достовірності побудованої поверхні;

–можливістю уточнювати отриманий результат на основі особистого досвіду експерта з урахуванням різноманітних додаткових факторів, які не могли бути відображені у вигляді вихідних даних.

Для безпосереднього створення інтерпольованої поверхні необхідний набір (мережа) точок з даними про їх просторове розміщення (координати x, y в декартовій системі або у вигляді широти / довготи в географічній системі)

ікількісне значення параметра z у цих точках (висота, тиск, температура, концентрація забруднювача тощо). Тобто для побудови інтерпольованої поверхні одним із методів, що є в арсеналі ГІС (IDW, Spline, Kriging, TIN тощо) на "вхід" утиліти інтерполяції потрібно подати набір (шар) точок.

Для більшості випадків мережа (набір, сітка) таких вихідних точок (data point) є нерегулярною (задана в деяких точках досліджуваної ділянки простору), має різну щільність, великі розриви тощо.

Завданням просторової інтерполяції є побудова на основі мережі ви-

хідних точок суцільної поверхні із заданим розміром кроку сітки вузлів, що розраховуються. Залежно від необхідної просторової точності вибирається

182

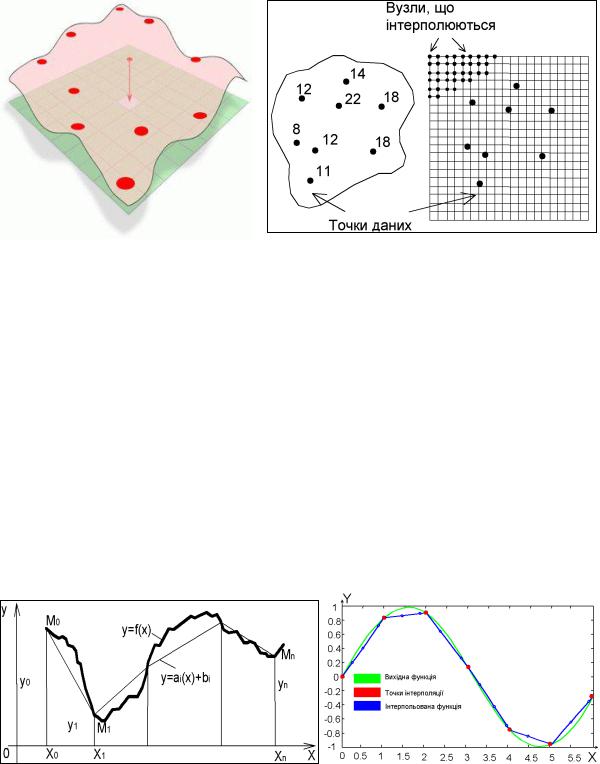
різний крок інтерполяції (наприклад, ділянка розміром 10х10 км може бути інтерпольована з кроком 100 м (100x100 вузлів сітки) або з кроком 10 м (1000x1000 вузлів). На підставі числових значень точок даних розраховується значення для кожного вузла мережі, що інтерполюється. Зазвичай процедура інтерполяції виконується для області прямокутної форми – растра (рис. 9.2).

Рис. 9.2. Приклад невпорядковано отриманих даних, для інтерполяції

Інтерполяція – відновлення функції на заданому інтервалі за відомими значеннями у кінцевій множині точок, що належать цьому інтервалу.

9.2. Створення поверхонь за допомогою лінійної інтерполяції

Лінійна інтерполяція – це інтерполяція функції f алгебраїчним двочленом P1(x) = kx + c у точках x0 та x1, які належать відрізку [a, b].

Якщо припустити, що приріст функції пропорційний приросту аргументу (лінійна інтерполяція), то функція заміняється ламаною, що складається з відрізків прямої, які з’єднують пари сусідніх значень. Вона полягає в тому, що задані точки М(xi,yi) (i = 0,1,...,n) з’єднуються прямолінійними відрізками і функція f(x) наближається до ламаної з вершинами у даних точках (рис. 9.3).

Рис. 9.3. Приклади лінійної інтерполяції

183

Інтерполяція не зводиться до заповнення значень функції для проміжних значень аргументу, а полягає в побудові за таблицею значень функції її аналітичного виразу, найчастіше багаточлена (полінома) ступеня на одиницю менше, чим кількість заданих значень (параболічна інтерполяція).

Формули для побудови такого багаточлена називаються інтерполяційними формулами. З них найчастіше застосовуються інтерполяційні формули Лагранжа, Ньютона, Бесселя, Стірлінга, Еверетта. За наявності в значеннях функції випадкових помилок треба віддати перевагу апроксимації функції багаточленами раціональними дробами, які мінімізують максимум абсолютної погрішності на всьому інтервалі. Рівняння кожного відрізку ламаної лінії в загальному випадку – різні. Оскільки маємо n інтервалів (xi, xi+1), то для кожного з них рівняння інтерполяційного полінома використовується рівняння прямої, що проходить через дві точки. Зокрема, для i-го інтервалу можна написати рівняння прямої, що проходить через дві точки (xi, yi) та (xi+1, yi+1), у вигляді:

xi 1 xi

Отже, при використанні лінійної інтерполяції спочатку потрібно визначити інтервал, у який потрапляє значення аргументу x, а потім підставити його в наведену формулу і знайти наближене значення функції в цій точці.

Інтерполяції й апроксимації використовуються, зокрема, в картографічному методі дослідження, математико-картографічному моделюванні і ГІС, у тому числі і в операціях обробки ЦМР для відновлення поверхонь за множиною її дискретних значень і проведення ізоліній (наприклад, горизонталей за сукупністю висотних позначок). Необхідність урахування особливостей, пов’язаних із просторовістю даних інтерполяції (сферичність Землі, викривлення картографічних проекцій тощо), дозволяє виділяти так звану просторову інтерполяцію з притаманними їй особливостями реалізації методів інтерполяції.

9.3. Інтерполяція на основі триангуляції Делоне

Інтерполяція на основі триангуляції Делоне за умови достатньо рівномірного розташування точок в точності моделює дії людини при побудові рельєфу в горизонталях і обчисленні висот точок, у результаті чого досягається найбільш звична картина рельєфу. При цьому спочатку будується

184