ТВ / МДЗ / MDZ2

МДЗ №2

по курсу “Теория вероятностей”

Выполнил студент факультета МП и ТК

Группы МП-22

Цыганов Илья

Таблица результатов

№	Тема	Ключевые слова	Зачет/незачет
266	Случайные величины	Описать закон распределения
281	Случайные величины	Тираж спортлото
296	Случайные величины	Закон Коши
311	Случайные величины	Бета-распределение
326	Независимые повторяемые испытания	Дожди в сентябре
341	Производящая функция	Стрельба по движущейся мишени
356	Распределение Пуассона	Опечатки
371	Нормальное распределение	Шарики для подшипников
386	Случайные векторы	Шары и ящики
401	Случайные векторы	Дефекты
416	Случайные векторы	Квадрат. Зависимость величин
431	Нормальное распределение	Эллипс рассеивания
446	Нормальное распределение	Ковариационная матрица
461	Функции случайных величин	Испытания Бернулли
476	Характеристическая функция	Биномиальное распределение
491	Характеристическая функция	Распределение Коши

Задача № 266.

Решение

	2	3	4
	0,3	0,2	0,5

Вычислим математическое ожидание

Вычислим дисперсию

Задача № 281.

Решение

При k=6 найдем вероятность как произведение вероятностей угадать номер из оставшихся номеров

При k=5 найдем вероятность как произведение вероятностей угадать номер из оставшихся

номеров, умноженной на количество способов выбрать 5 выигрышных номеров из 6

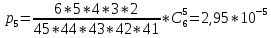
Задача № 296.

Ответ:

Решение

Для вычисления моды найдем вторую производную функции и приравняем её к нулю

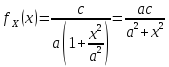
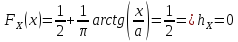
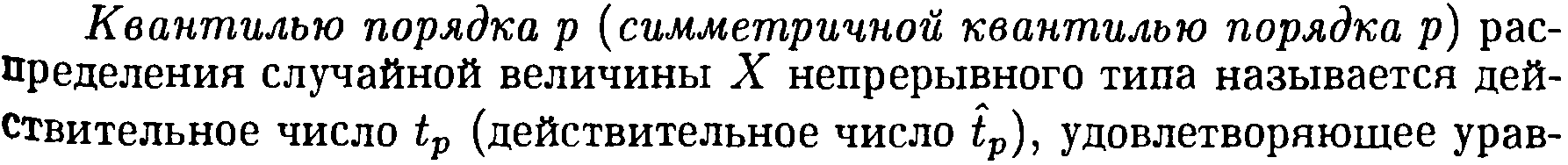
Задача № 311.

Решение

Плотность бета - распределения выражается формулой

Здесь мы воспользовались тем, что

Задача № 326.

Решение

Вероятность что наугад взятый день дождливый 

Вероятность того, что из 6 наугад выбранных дней 2 дождливых

Вероятность того, что из 6 наугад выбранных дней 3 дождливых

То есть, вероятность, что из восьми наудачу выбранных дней будет 3 дождливых, больше.

Задача № 341.

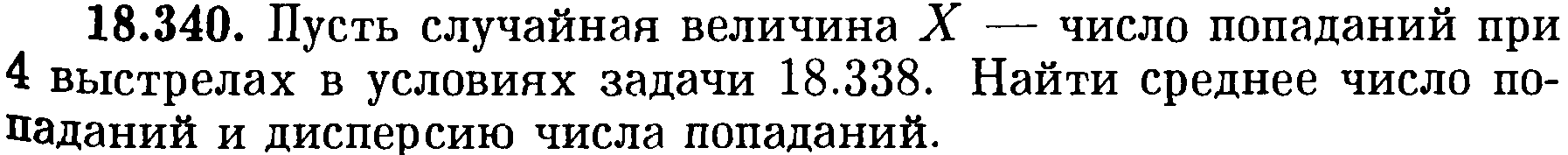
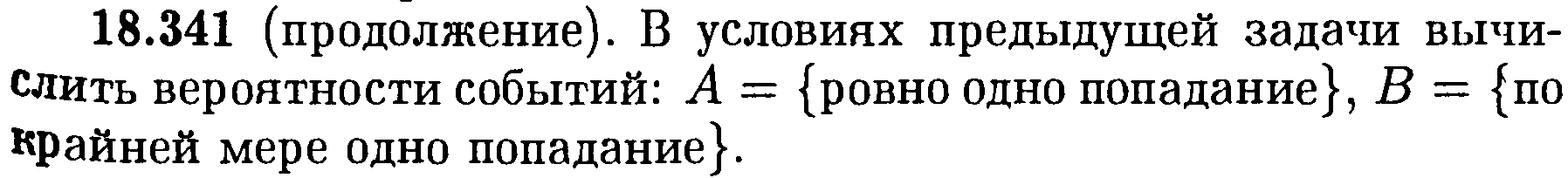
Решение

Составим производящую функцию

Тогда равна коэффициенту перед

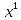
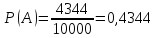
Для вычисления вероятности события B перейдем к противоположному событию

Задача № 356.

Решение

Так как и то можно считать, что случайное число опечаток подчиняется распределению Пуассона с параметром .

Данную формулу можно представить в рекуррентном виде

Очевидно, что наиболее вероятное число опечаток будет на последнем шаге, когда

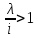
т. е.

Задача № 371.

Ответ:

Решение

Чтобы определить значение параметра решим уравнение

Из таблицы значений функции находим, что

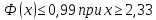
Задача № 386.

Решение

x\y	0	1	P{X=xi}
0	0,16	0,24	0,4
1	0,24	0,36	0,6
P{Y=yi}	0,4	0,6

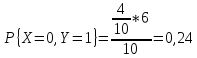
Событие {X>Y} эквивалентно событию {X=1, Y=0}

В условии задачи 18.385

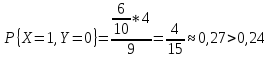
Т.е. вероятность события {X>Y} больше в условиях задачи 18.385

Задача № 401.

Решение

Введем индикаторные случайные величины:

x\y	0	1	P{X=xi}
0	0,95	0,02	0,97
1	0,005	0,025	0,03
P{Y=yi}	0,955	0,045

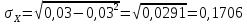
Задача № 416.

Решение

Так как распределение равномерное, то

Вычислим плотность распределения отдельных компонент

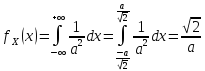
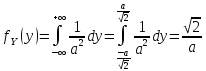
Следовательно, величины зависимы

Задача № 431.

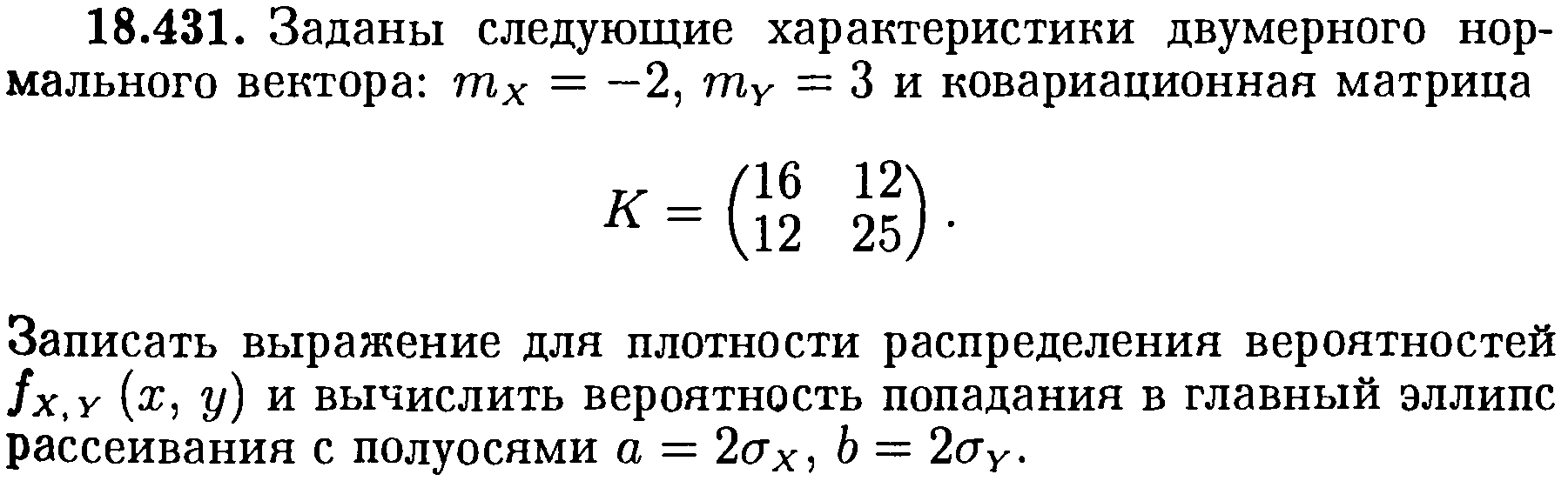
Решение

Из ковариационной матрицы находим, что

Уравнение эллипса

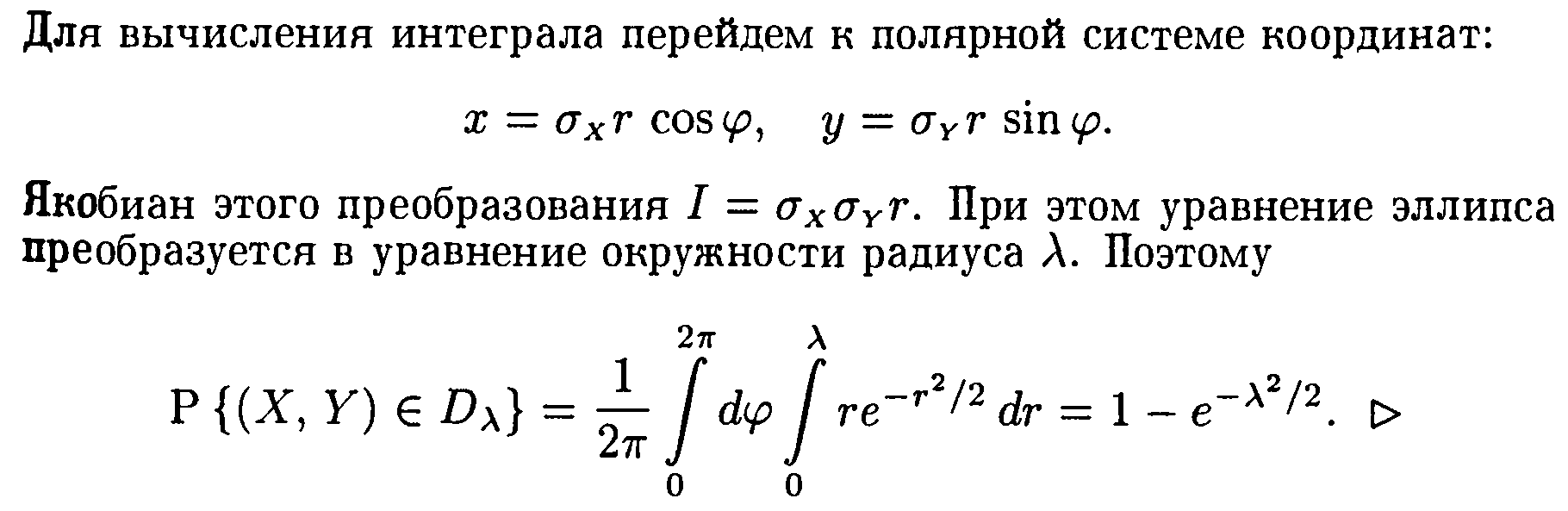
Подставляя , получаем

Задача № 446.

Решение

Также воспользуемся выражением начальных моментов через центральные

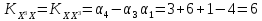
Ковариационная матрица будет выглядеть следующим образом

Задача № 461.

Решение

Задача № 476.

Решение

Здесь мы воспользовались формулой бинома Ньютона

Задача № 491.

Решение

Для каждого 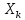характеристическая функция выглядит следующим образом

Тогда

что соответствует распределению Коши с параметрами с=0 и а=1

Задача № 506.

Решение

Задача № 521.

Решение

Задача № 536.

Решение