Bilety_Metrologia

33.Оценка истинного значения измеряемой величины с помощью доверительных интервалов с помощью

44.Погрешности измерительных приборов по соотношению быстродействия СИ и скоростью изменения

1. Этапы развития метрологии.

Древнейшие измерения. Продолжался до конца XVIII в.

Характеризуется развитием таких отношений, как:

отношение эквивалентности (равно / не равно);

отношение порядка (больше / меньше);

метрические отношения (во сколько раз больше/меньше).

Используемые единицы измерения: Локоть ~ 0,5 м; Сажень ~ 2,135 м; Ладонь ~ 10,16 см; Фут ~ 30,48 см.

Причины к поднятию вопросов о единстве измерений (эталонах) и единообразии средств измерений:

большое количество единиц измерения одних и тех же величин (локоть, сажень, ладонь);

их непостоянство (меняли свое значение в зависимости от того кто проводил измерения).

Единство измерений – состояние измерений, при котором их результаты выражены в узаконенных единицах и погрешности измерений известны с заданной вероятностью (ГОСТ 16263-70).

Единообразие средств измерений – состояние средств измерений, характеризующееся тем, что они проградуированы в узаконенных единицах и их метрические характеристики соответствуют нормам (ГОСТ 1626370).

Ввод метрической системы мер – обеспечение международного единообразия мер. Продолжался до 3й четверти XIX в.

Характеризуется осознанием необходимости обеспечения единообразия мер (создание метрической системы мер).

1791 г. – Национальное собрание Франции принимает метрическую систему мер.

научная организация, позднее преобразована во Всесоюзный Ордена Трудового Красного Знамени НИИ Метрологии имени Д.И. Менделеева.

1955 г. – В СССР организован второй крупнейший НИИ, который занимался созданием и хранением эталонов в области радиоэлектроники, службы времени и частоты, акустики – Всесоюзный Научно-исследовательский Физико-технический и Радиотехнический Институт (ВНИФТРИ).

Становление метрологии как самостоятельной науки. Продолжался до середины XX в.

Метрология («метро» – мера; «логос» – закон) – наука об измерениях, методах и средствах обеспечения их единства, и способах достижения требуемой точности.

Метрология как наука изучает следующие вопросы:

общая теория измерений;

физические величины и их системы;

методы и средства измерений;

способы определения точности измерений;

основы обеспечения единства измерений и единообразия средств измерения;

эталоны и образцовые средства измерений;

методы передачи размеров единиц от эталонов и образцовых средств измерений рабочим средствам измерений.

Регламентация измерений как вида производственной и научной деятельности.

Законодательная метрология – раздел метрологии, включающий комплексы взаимосвязанных и взаимообусловленных общих правил, требований и норм и другие вопросы, нуждающиеся в регламентации и контроле со стороны государства, и направленные на обеспечение единства и единообразия средств измерения.

Главный орган, осуществляющий контроль за измерениями – Госстандарт. Современные измерения характеризуются двумя спецификациями:

необходимость выполнения одновременного измерения нескольких величин;

очень часто эти измерения необходимо производить в реальном времени.

Три основных понятия: ВЫЧИСЛЕНИЕ, УПРАВЛЕНИЕ, ИЗМЕРЕНИЕ разделить невозможно.

Измерения невозможно осуществлять без создания средств на базе вычислительной техники. Вычислительные средства невозможно разрабатывать, настраивать и эксплуатировать без измерительных средств.

2. Понятия физической величины, значения величины, истинного и действительного значений. Размерность физической величины.

Физическая величина – свойство, в качественном отношении присущее многим физическим объектам, их системам, многим протекающим в них процессам, но в количественном отношении индивидуальное для каждого физического объекта.

Значение физической величины - оценка величины в виде некоторого числа принятых для неё единиц.

Q = q [Q],

где Q – значение величины, q – численное значение, [Q] – единица физической величины (например,

R= 200 Ом).

Различают:

Истинное значение величины – значение величины, которое в качественном и количественном отношении

идеально отражало свойство объекта.

Действительное значение величины – значение величины, найденное эксперимент путём и настолько приближающееся к истинному значению, что для данной цели может быть принято вместо него.

Все физические величины как-то связаны между собой. Эту связь можно записать в виде уравнений – уравнений связи.

Если n - количество величин; m - количество уравнений связи, то n > m.

Выделяют k n m – физических величин, которые не определяются другими физическими величинами – это основные физические величины, а остальные называются производными физическими величинами.

Формальных правил по выделению основных величин не существует, единственный критерий – это удобство изготовления эталонов.

Размер физической величины – это количество данного свойства, содержащегося в объекте измерения. Размерность физической величины – это выражение, показывающее, во сколько раз изменяется размер

производной величины, если размер основной величины изменился в несколько раз.

3. Физические величины и их единицы. Системы единиц величин.

Физическая величина – свойство, в качественном отношении присущее многим физическим объектам, их системам, многим протекающим в них процессам, но в количественном отношении индивидуальное для каждого физического объекта.

Система физических величин – совокупность взаимосвязанных физических величин, образованная по принципу, когда одни физические величины являются независимыми (основными физическими величинами), а другие являются их функциями (производными физическими величинами).

Если коэффициент пропорциональности основных и производных единиц k=1, то система называется

когерентной. Если k 1, то система не когерентна.

Первая традиционная метрическая система – система, принятая Национальным собранием Франции в 1791г.

несовершенна

включены много лишних производных величин

не когерентна (все минимальные системы единиц не когерентны) Первая минимальная система предложена Карлом Гауссом в 1832г.

в нее входили три основные величины LMT.

названа абсолютной, т.е. меньше не бывает.

первая такая система – СГС (сантиметр, грамм, секунда) (1881 г.)

Единица силы F – дина, а энергии E – эрг.

хороша для физики, но неудобна для электричества.

–не когерентна;

–единицы производных величин в этой системе имеют размер совершенно с практической точки зрения не потребные.

Это несовершенство привело к тому, что система СГС имеет семь модификаций. Тогда же приняли систему практических единиц (Ом, Вольт, Ампер и т.д.).

Система МКГСС:

основные единицы – метр, килограмм силы, секунда.

хороша для решения задач, где надо найти силу.

недостаток : эталон килограмма силы найти невозможно. Определялся он как сила, приложенная к эталону массы таким образом, что она приобретает ускорение 1g.

В1955г формируется– СИ (SI). Целью - устранение недостатков всех уже существующих систем единиц.

не минимальна.

состоит из 7 основных единиц, 2 дополнительных и таблицы дольных и кратных приставок.

4. Международная система единиц СИ.

Основные единицы:

1 м = 1650763,7 – длин волн в вакууме излучения атома криптона-86 при переходе 2p10 5d5 1 кг – это гиря, которую сделали 1875г, здесь ничего не изменили.

1 с = 9.192.631.770 периодов колебаний излучения цезия-133.

1 А – это сила электрического тока, который, протекая по двум параллельным проводникам бесконечно малого сечения и бесконечной длины, расположенных на расстоянии 1 м друг от друга, создаёт силу 2 10 7 H .

1K 273.161 температуры тройной точки воды (температура, при которой вода в чистом виде находиться в 3-х агрегатных состояниях).

1 Кандела – это сила света испускаемого идеальным источником (абсолютно черным телом) в направлении

платины и при нормальном давлении, которое составляет 101325 Па.

1 моль – это такое количество вещества, в котором содержится столько молекул или атомов или частиц, сколько атомов содержится в нуклиде углерода-12 массой 0,012кг. Как трактовать или молекул, или атомов, или частиц? Если вещество имеет молекулярную структуру, то нужно брать молекулы, если молекулярной структуры нет, то количество атомов, а если и атомарной структуры нет (например, в плазме), то количество частиц.

Дополнительные единицы:

1 радиан 5717'44,8'' - это угол, образованный в окружности двумя радиусами и вырезающий в этой окружности дугу длиной равной радиусу.

1 стерадиан = 65 32' это такой телесный угол, помещённый в центр сферы, у которого длина образующих равна радиусу сферы (получается конус) и он вырезает на поверхности сферы некоторую фигуру, которая должна иметь площадь равную площади квадрата со стороной, равной радиусу сферы.

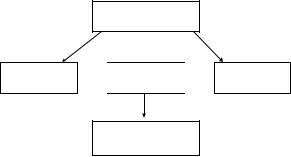
5. Понятие измерения. Измерительные отношения.

Схема измерения

Количественное содержание какого-то свойства называется мерой. Определение по схеме:

Измерение – это сравнение искомой величины с ей подобной принятой за единицу.

Определение по ГОСТу: Измерение – это нахождение значения величины опытным путём с помощью специальных технических средств.

Измерительное отношение – отношение искомой величины к подобной, принятой за единицу.

Процесс измерения мы можем трактовать как отображение множества состояний объекта измерений в множество результатов.

6. Измерительное отображение. Свойства измерительного отображения.

Схема измерений:

:→ ,

где X – множество состояний объекта измерений, А – мн-во результат измерений, J – измерительное отображение.

:

Отображение – некая «функция», связь между состоянием объекта и результатом измерения. Обратное отображение:

Промежуточные отображения:

→&&

7. Классификация измерений. Виды измерений. Примеры.

Виды измерений:

1.Косвенные – определение искомого значения физической величины на основании результата прямых измерений других физических величин, функционально связанных с искомой величиной. (+ расчет => прямые)

Пример: если измерить силу тока амперметром, а напряжение вольтметром, то по известной функциональной взаимосвязи всех трёх величин (сила тока, напряжение, мощность) можно рассчитать мощность электрической цепи.

2.Совместные – это измерения 2+ неоднородных физических величин для определения зависимости между ними.

Пример: измерение температурного коэффициента линейного расширения. Измерение изменения температуры образца испытываемого материала и соответствующего приращения его.

3.Совокупные – проводятся одновременные измерения нескольких одноименных величин, при которых искомое значение величин определяется путем решения системы уравнений, получаемых при измерениях этих величин в различных состояниях. (+ система уравнений => прямые)

Пример: измерение сопротивлений резисторов, соединенных треугольником, путем измерений сопротивлений между различными вершинами треугольника; по результатам трех измерений определяют сопротивления резисторов.

Прямое измерение – измерение, при котором искомое значение физической величины получается непосредственно.

Все виды измерений сводятся у прямым.