-
Типы отверстий в печатных платах, обработка контура печатной платы, учет технологии изготовления при проектировании печатной платы.
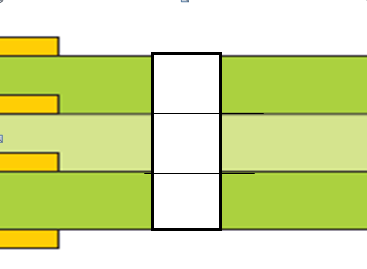
НЕМЕТАЛЛИЗИРОВАННЫЕ (монтажные)
(Mounting Hole) Nonplated
МЕТАЛЛИЗИРОВАННЫЕ СКВОЗНЫЕ
(Through Hole) Plated
ПЕРЕХОДНЫЕ (VIA)
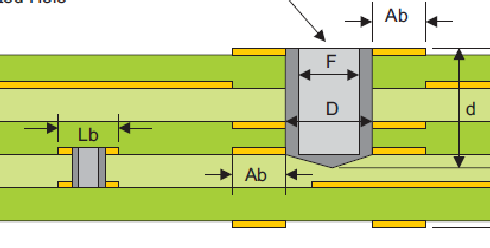
«Скрытые», «погребенные» (BURIED VIA) -
позволяют наиболее продуктивно использовать поверхность наружных слоев платы, не засоряя ее локальными переходами.
«Глухие», «слепые»
(BLIND VIA)
В двусторонней печатной плате (в отличие от односторонней) кроме неметаллизированных отверстий могут быть и металлизированные. Если в эти отверстия в дальнейшем будут установлены и припаяны проволочные выводы элементов, то такие отверстия принято называть сквозными контактными площадками (Pad), они, кстати, не закрываются при изготовлении паяльной маской. Если же отверстия служат только для электрического соединения проводников верхнего и нижнего слоев, то их называют переходными отверстиями (Via), при этом диаметр отверстия стараются взять минимально возможным, чтобы не занимать лишнего места на печатной плате.
Обработка плат по контуру осуществляется после штамповки фрезерованием, алмазной резкой, резкой на гильотинах или штамповкой. В условиях опытного нли мелкосерийного производства целесообразно применять обрезку по контуру с помощью алмазных или абразивных кругов. Проверку производят сличением с эталоном при помощи лупы/микроскопа.
-
Основные понятия теории графов: ориентированные и неориентированные графы, связность, изоморфизм, клики, деревья, двудольные графы.
Ориентированный граф определяется как пара (V, E), где V - конечное множество вершин графа, а Е – множество дуг - подмножество множества V х V.
В неориентированном графе G = (V,E) множество Е называют множеством рёбер графа. Множество Е состоит из неупорядоченных пар вершин: парами являются множества {и, v}, где и, v є V и и ≠ v.
Неориентированный граф называется связным, если для любой пары вершин существует путь из одной в другую. Ориентированный граф называется сильно связным, если из любой его вершины достижима (по ориентированным путям) любая другая.
Классы эквивалентности называются связными компонентами графа. Неориентированный граф связен тогда и только тогда, когда он состоит из единственной связной компоненты, ориентированный граф сильно связен тогда и только тогда, когда состоит из единственной сильно связной компоненты. Любой ориентированный граф можно разбить на сильно связные компоненты.
Два графа G = (V, Е) и G' = (V',Е') называются изоморфными, если существует взаимно однозначное соответствие f: V → V' между множествами их вершин, при котором рёбрам одного графа соответствуют рёбра другого. Можно сказать, что изоморфные графы - это один и тот же граф, в котором вершины названы по-разному.
П
олным
графом называют неориентированный
граф, содержащий все возможные рёбра
для данного множества вершин (все
вершины попарно смежны). Соответственно,
граф, в котором все вершины попарно
несмежны, называют пустым. Полный
подграф, не являющийся подграфом другого
полного подграфа называется максимальным
полным подграфом или кликой. Граф
на рис.1.3 содержит три клики: {x1, x2, x5,
x6}, { x2, x3, x6} и { x3, x4}.
Неориентированный граф (V,Е) называют двудольным, если
множество вершин V можно разбить на две части V1 и V2 таким образом, что
концы любого ребра оказываются в разных частях (подграфы, порожденные
множествами вершин V1 и V2, являются пустыми).
Ациклический неориентированный граф называют лесом, а связный
ациклический неориентированный граф называют деревом.