Тема 3.Кривые линии и поверхности. Позиционные задачи

1. Классификация поверхностей

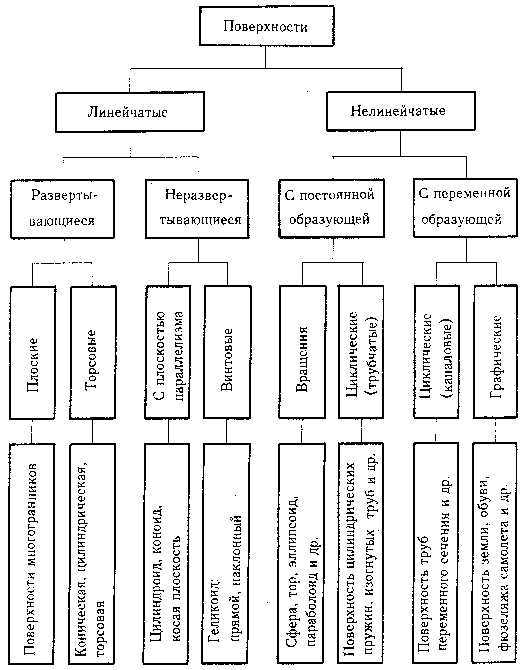
Линейчатые поверхности - поверхности, которые могут быть образованы с помощью прямой линии.

Нелинейчатые поверхности - поверхности, которые могут быть образованы только с помощью кривой линии.

Развертывающиеся поверхности - поверхности, которые после разреза их по образующей могут быть совмещены с плоскостью без наличия разрывов и складок.

Неразвертывающиеся поверхности - поверхности, которые не могут быть совмещены с плоскостью без наличия разрывов и складок.

Поверхности с постоянной образующей - поверхности, образующая которых не изменяет своей формы в процессе образования поверхности.

Поверхности с переменной образующей - поверхности, образующая которых изменяется в процессе образования поверхности.

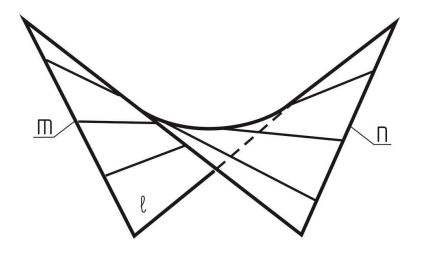
2. Линейчатые поверхности, имеющие две направляющие (пов-ти Каталана)

Поверхности данной группы образуются при движении в пространстве прямой образующей ℓ по двум направляющим m и n. В этом случае необходимо добавить условие, которое должна выполнять прямолинейная образующая в процессе своего движения. Чаще всего в качестве такого условия применяется условие параллельности образующей l некоторой плоскости Г. 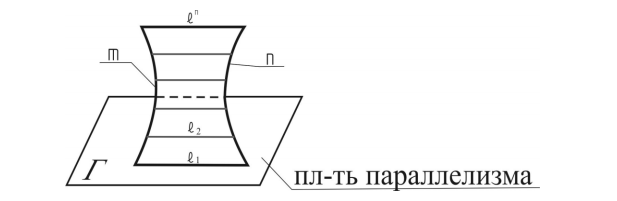Такая плоскость называется плоскостью параллелизма, а линейчатая поверхность, заданная таким способом – линейчатой поверхностью с плоскостью параллелизма или поверхностью Каталана.Определитель данных поверхностей: Σ (m, n, Г), где Σ – поверхность; m и n – направляющие; Г – плоскость параллелизма.

В эту группу входят поверхности:

1. Поверхность прямого цилиндроида. Такая поверхность может быть образована движением прямолинейной образующей по двум направляющим т и п в том случае, когда они – гладкие кривые линии, причем одна из них – плоская кривая, плоскость которой перпендикулярна плоскости параллелизма Г.

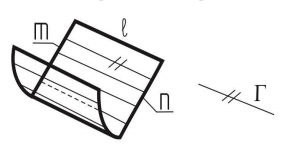
2. Поверхность прямого коноида. Эта поверхность получается в том случае, когда одна направляющая – кривая линия, а вторая – прямая, причем она перпендикулярна плоскости параллелизма Г. Поверхность прямого коноида используется в гидротехническом строительстве для формирования поверхности устоев мостовых опор.

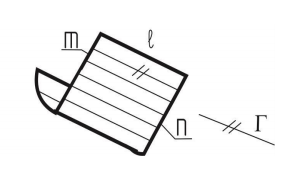
3. Поверхность гиперболического параболоида (гипар). Такая поверхность образуется в том случае, когда две направляющие – скрещивающиеся. Поверхность косой плоскости применяется в инженерно-строительной практике для формирования поверхностей откосов, насыпей, железнодорожных и автомобильных дорог, набережных, гидротехнических сооружений в местах сопряжения откосов, имеющих различные углы наклона.

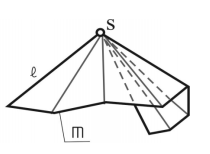
3. Линейчатые поверхности с одной направляющей

Данные поверхности образуются движением прямой образующей, один конец которой проходит через неподвижную точку S, а второй – перемещается по направляющей m. В зависимости от того, какой линией является направляющая, образуется тот или иной вид поверхности. Определитель такой поверхности имеет вид: Σ (S, m), где S – конечная точка; m – направляющая

К ним относятся следующие поверхности.

1. Поверхность с ребром возврата.Эта поверхность образуется движением прямолинейной образующей, во всех своих положениях касательной к пространственной кривой, называемой ребром возврата.

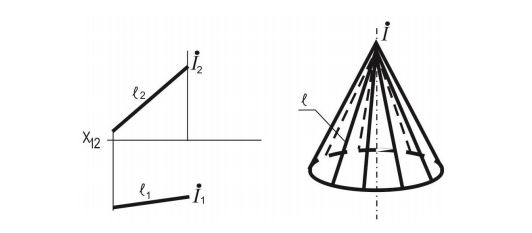
2. Коническая поверхность. Эта поверхность образуется движением прямолинейной образующей, скользящей по кривой, направляющей m и проходящей во всех своих положениях через одну и ту же неподвижную точку S

3. Пирамидальная поверхность. Эта поверхность образуется движением прямолинейной образующей, скользящей по ломаной направляющей m и проходящей во всех своих положениях через одну и ту же неподвижную точку S.

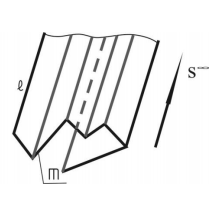
4. Цилиндрическая поверхность. Данная поверхность образуется движением прямолинейной образующей ℓ, по криволинейной направляющей m, при условии, что S^∞бесконечно удалена (т.е. все образующие двигаются относительно друг друга параллельно).

5. Призматическая поверхность. Эта поверхность образуется движением прямолинейной образующей, скользящей по ломаной направляющей m и проходящей во всех своих положениях через одну и ту же неподвижную точку S^∞.

4. Линейчатые поверхности вращения

1 Цилиндрическая поверхность вращения. Эта поверхность может быть получена вращением прямой, параллельной оси вращения i

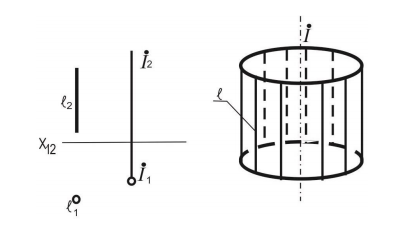
2 Коническая поверхность вращения. Поверхность конуса вращения может быть получена вращением прямой, пересекающей ось вращения i

5. Циклические поверхности вращения

Поверхности вращения получили широкое применение в архитектуре и строительстве. Поверхностью вращения называют поверхность, получаемую вращением какой-либо образующей линии вокруг неподвижной прямой – оси вращения поверхности. Плоскости, перпендикулярные оси вращения, пересекают поверхность по окружностям – параллелям. Наименьшую параллель называют горлом, наибольшую – экватором. Линии, по которым плоскости, проходящие через ось вращения, пересекают поверхность, называют меридианами. Каждый меридиан разделяется на две симметричные относительно оси вращения линии, называемые полумеридианами. Меридиан, расположенный в плоскости, параллельной фронтальной плоскости проекций, называют главным меридианом. Определитель поверхности вращения: Σ (i, ℓ), где i – ось вращения; ℓ – образующая.

Здесь образующей является плоская кривая ABCD, ось вращения i расположена в одной плоскости с этой кривой. Основные свойства поверхности вращения таковы.

1 Отрезок меридиана между двумя точками поверхности есть кратчайшее расстояние между этими точками.

2 Все меридианы равны между собой.

3 Каждая из параллелей поверхности вращения пересекает меридианы под прямым углом. Поверхности вращения на чертеже удобно задавать очерками, проекциями ее характерных линий и точек. Фронтальным очерком поверхности вращения является фронтальная проекция главного меридиана, а горизонтальным – горизонтальная проекция экватора.

Рассмотрим основные виды поверхностей вращения.

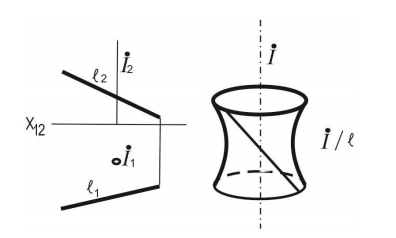
1 Однополостный гиперболоид вращенияобразуется при вращении линии вокруг мнимой оси

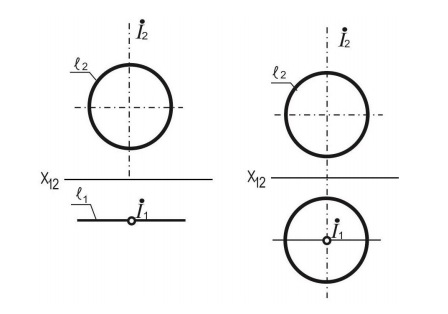
2 Сфера (шар).Образующая сферы – окружность, центр которой О находится на оси вращения i

3 Тор. Образующая тора – окружность или ее дуга. Ось вращения i лежит в плоскости этой окружности, но не проходит через ее центр (рис. 85). Различают

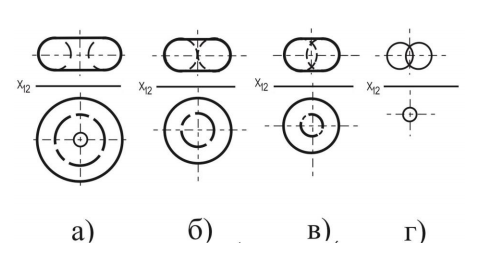
открытый тор (круговое кольцо) (рис. 85а, б),

закрытый (рис. 85 б),

самопересекающийся (рис. 85 в, г).

Образующей для открытого (рис. 85 а) и закрытого тора (рис. 85 б) служит окружность, для самопересекающегося (рис. 85 в, г) – дуга окружности.

4 Параболоид вращения.Такая поверхность образуется при вращении параболы вокруг ее оси. Поверхность параболоида используется в параболических антеннах и зеркалах рефлекторов.

5 Гиперболоид вращения. Эта поверхность образуется при вращении гиперболы вокруг оси. Различают двуполостный и однополостный гиперболоид вращения. Для двуполостного гиперболоида вращения осью вращения служит действительная ось гиперболы (рис. 87), для однополостного гиперболоида (рис. 88) – ее мнимая ось. Однополостный гиперболоид вращения также может быть образован вращением прямой линии в случае, если образующая и ось вращения – скрещивающиеся прямые.

6 Эллипсоид вращенияобразуется, если сферу сжать или растянуть вдоль одного из диаметров, его меридианом является эллипс. Если эллипс вращается вокруг большой оси, эллипсоид называется вытянутым (рис. 89а); если вращение происходит вокруг малой оси, эллипсоид называется сжатым или сфероидом (рис. 89б).

Положение точки на поверхности вращения определяется с помощью окружности, которая проходит на поверхности вращения через эту точку. В случае линейчатых поверхностей вращения (цилиндр, конус) возможно использование для этой цели прямолинейных образующих.

6. Прямая и плоскость, касательные к поверхности

Касательные плоскости играют большую роль в геометрии. В теоретическом плане плоскости, касательные к поверхности, используются в дифференциальной геометрии при изучении свойств поверхности в районе точки касания.

Решение задач, возникающих при проектировании и конструировании поверхностей-оболочек, требует проведения касательных плоскостей и нормалей к поверхности. При построении на проекционном чертеже очерков поверхностей по заданному направлению проецирования, при определении контуров собственных теней также необходимо строить касательные плоскости к поверхности. Построение касательной плоскости к поверхности представляет частный случай пересечения поверхности плоскостью.

Плоскость, касательная к поверхности, имеет общую с этой поверхностью точку, прямую или плоскую кривую линию. Плоскость в одном месте может касаться поверхности, а в другом пересекать эту поверхность. Линия касания   может одновременно являться и линией пересечения поверхности плоскостью.

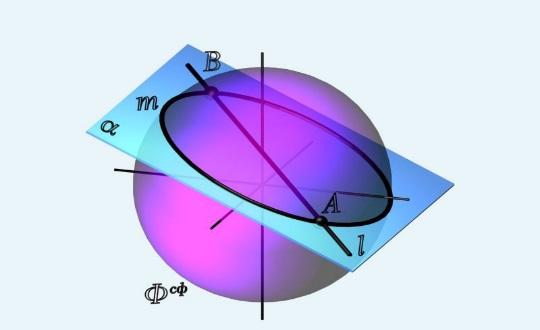
Плоскость α (рис.123), представленную двумя касательными, проведенными в точке А поверхности Ф, называется касательной плоскостью к поверхности в данной ее точке.

Любая кривая поверхности, проходящая через точку А, имеет в этой точке касательную прямую, принадлежащую плоскости α.

Не в каждой точке поверхности можно провести касательную плоскость. В некоторых точках касательная плоскость не может быть определена или не является единственной. Такие точки называются особыми точками поверхности, например, вершина конической поверхности.

Прямую линию, проходящую через точку касания и перпендикулярную касательной плоскости, называют нормалью поверхности в данной точке.

ВИДЫ КАСАНИЯ

В зависимости от вида поверхности, касательная плоскость может иметь с поверхностью как одну общую точку, так и множество точек. В зависимости от того, с каким случаем касания, мы имеем дело, точки, принадлежащие поверхности подразделяют на эллиптические, параболические и гиперболические:

Если касательная плоскость имеет с поверхностью только одну общую точку, то все принадлежащие поверхности линии, проходящие через эту точку, будут расположены по одну сторону от касательной плоскости (рис.123). Такие точки называются эллиптическими.

В случае проведения касательной плоскости к торсовой поверхности, образованной непрерывным перемещением касательной прямой к некоторой пространственной кривой линии (частный случай - коническая поверхность), плоскость будет касаться поверхности по прямой линии – образующей. Точки, принадлежащие этой образующей, называются параболическими (рис.124).

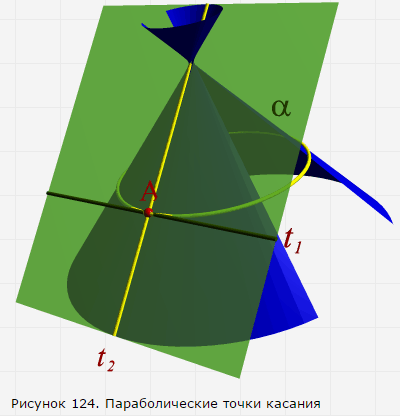
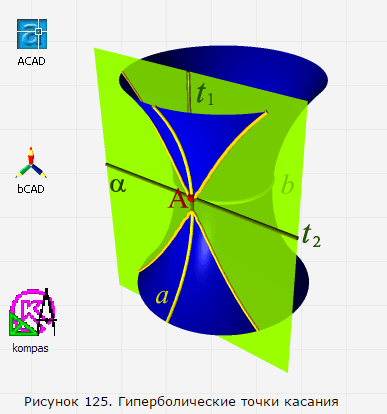
Точки поверхности, в которых касательная плоскость пересекает поверхность, называют гиперболическими (рис.125). Гиперболическая точка принадлежит линии, по которой касательная плоскость пересекает поверхность.

7. Пересечение поверхности с плоскостью способом нормальных сечений

Этот способ удобно применять, если на чертеже боковые ребра призмы являются линиями уровня.

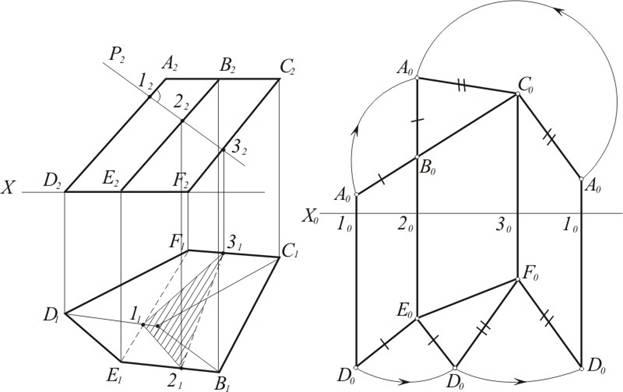
П р и м е р 1 . Построить развертку наклонной трехгранной призмы ABCDEF (рис. 6)

Р е ш е н и е . Решение начинаем с построения развертки боковой поверхности заданной призмы. По условию боковые ребра призмы параллельны плоскости π2. Пересечем призму плоскостью γ (γ′′), перпендикулярной ее боковым ребрам. Сечение призмы такой плоскостью называется н о р м а л ь н ы м. 9 Определим натуральный вид нормального сечения (на рис. 6 это сделано с помощью замены плоскости π1 на плоскость π3 || γ). Зная величины сторон нормального сечения и длины боковых ребер, можно определить натуральный вид каждой грани и обоих оснований призмы и построить ее развертку.

Для этого:

1. На произвольной прямой а0 откладываем отрезки 1020, 2030, 3010, конгруэнтные сторонам 123 (спрямляем нормальное сечение);

2. Через точки 10, 20, 30, 10 проводим прямые, перпендикулярные прямой m0, и откладываем на них отрезки 10А0, 10D0, 20B0 и т.д., равные отрезкам 1A, 1D, 2B и т.д. боковых ребер призмы, с учетом их расположения по отношению к плоскости γ (справа или слева);

3. Полученные точки А0, В0, С0, А0 и D0, E0, F0, D0 соединяем отрезками прямой линии. Плоская фигура А0В0С0А0D0E0F0D0 представляет собой развертку боковой поверхности призмы, построенную способом нормального сечения. Для получения полной развертки призмы к развертке боковой поверхности пристроены основания призмы - ∆ А0В0С0 и ∆ D0E0F0.

8. Пересечение поверхности с прямой частного и общего положения

Прямая по отношению к поверхности может занимать следующие положения:

• • прямая касается поверхности (одна общая точка);

• • прямая пересекает поверхность (две и более общих точек);

• • прямая не пересекает и не касается поверхности (общих точек нет).

Алгоритм решения задач об определении взаимного положения поверхности и прямой аналогичен решению первой позиционной задачи (рис. 98):

• 1. Прямая заключается во вспомогательную плоскость частного положения.

• 2. Определяется линия пересечения вспомогательной плоскости и заданной поверхности, то есть, строится сечение поверхности вспомогательной плоскостью.

• 3. Определяется взаимное положение полученной линии (сечения) и заданной прямой. Точки пересечения являются искомыми точками пересечения прямой с поверхностью.

• 4. Определяется видимость прямой относительно поверхности.

Для построения точки пересечения поверхности сферы с горизонталью (рис. 99), горизонталь заключают во вспомогательную горизонтальную плоскость уровня γ(γ₂).

Сечение сферы горизонтальной плоскостью уровня представляет собой окружность l с центром в точке O₂ и радиусом r = O₁ l₂, которая проецируется на П₁ без искажения. Затем определяются точки пересечения окружности l₁ и заданной горизонтали h₁ :

Для построения точки пересечения поверхности закрытого тора с прямой общего положения (рис. 100), прямую заключают во вспомогательную фронтально-проецирующую плоскость δ(δ₂). Далее строится сечение тора плоскостью δ(δ₂):

Точки 1 и 2 – точки пересечения с основанием и точка 3 – опорные точки на очерковой образующей определяются без дополнительных построений;

Точки 4 и 5 также опорные (лежат на образующих, проекции которых совпадают с осью тора). Точки 4 и 5 определяются как точки на поверхности тора с помощью вспомогательной плоскости γ'.

Промежуточные точки 6,7,8,9 определяются аналогично.

Полученные точки соединяются плавной лекальной кривой m. Линия m – сечение тора плоскостью δ(δ₂). Затем определяют точки A и B пересечения полученной линии m с прямой a и определяют видимость. Точки A и B – искомые точки пересечения прямой с поверхностью тора.

• 1. a(a₁, a₂) ∈ δ(δ₂);

• 2. m = δ(δ₂)∩ Ф^т;

γ(γ₂) – вспомогательная плоскость;

γ(γ₂) ∩ Ф^т = l; l₂ = γ₂, l₁ – окружность;

γ(γ₂)∩ δ(δ₂) = p; p ⊥ П₂;

l×p = 6, 7 – промежуточные точки сечения m;

m×a = A, B – искомые точки пересечения прямой с поверхностью тора;

• 3. Определить видимость прямой относительно поверхности тора.

9. Решение задач по взаимному пересечению поверхностей с использование вспомогательных плоскостей и вспомогательных секущих сфер

Линия пересечения двух поверхностей представляет собой в общем случае пространственную кривую. Любая точка этой линии принадлежит как первой, так и второй поверхностям и может быть определена в пересечении линий, проведенных на этих поверхностях.

Исходя из этого, можно предложить следующие варианты решения задачи:

1) выбрать на одной из поверхностей конечное число линий и построить точки пересечения их с другой поверхностью;

2) выделить на заданных поверхностях два семейства линий и найти их точки пересечения.

Во втором варианте выделение пересекающихся пар кривых выполняют с помощью вспомогательных поверхностей-посредников, из которых наибольшее применение нашли плоскости и сферы. Поверхности-посредники выбирают таким образом, чтобы в пересечении их с заданными поверхностями находились графически простые линии или линии, которые проецировались бы в графически простые.

Так, способ концентрических сфер применяют в случае, если:

1) заданные поверхности – поверхности вращения;

2) оси поверхностей вращения пересекаются;

3) общая плоскость симметрии поверхностей параллельна какой-либо плоскости проекций (если это условие не выполняется, то следует использовать преобразование чертежа).

Другой способ – способ эксцентрических сфер применяют при условии, что:

1) одна из поверхностей – поверхность вращения, а другая имеет семейство окружностей;

2) поверхности имеют общую плоскость симметрии;

3) общая плоскость симметрии поверхностей параллельна плоскости проекций (в противном случае следует применить преобразование чертежа).

В целом алгоритм решения задачи на пересечение поверхностей включает следующие этапы:

1. Анализ исходных поверхностей с целью выбора поверхности- посредника.

2. Построение характерных (опорных) точек проекций линии пересечения поверхностей.

3. Построение промежуточных точек.

4. Установление видимости проекций линии пересечения поверхностей. 5. Оформление чертежа.