ВВЕДЕНИЕ В ИНЖЕНЕРНУЮ ГРАФИКУ

1. Условия образования и свойства комплексного чертежа Комплексным чертежом называется чертеж, составленный из двух или более связанных между собой ортогональных проекций изображаемого геометрического образа.

Принцип образования: геометрический образ ортогонально проецируется минимум на две взаимно перпендикулярные плоскости проекций, которые затем соответствующим образом совмещаются с одной плоскостью. Если на К.Ч. заданы две проекции точки, можно утверждать, что точка однозначно задана на К.Ч. Данный чертеж называется комплексным чертежом (К.Ч.) точки А.

Чертёж должен быть:

1. Обратимым

2. Наглядным

3. Простым

2. Образование и закон проекционной связи 2х картинного комплексного чертежа

Двух картинный комплексный чертёж точки (эпюр точки) образуется путём совмещения П1 и П2 (горизонтальной и фронтальной плоскостей), при этом П1, вращаясь вокруг оси Х, опускается вниз до совмещения с плоскостью П2.

Закон проекционной связи:

1. Горизонтальная и фронтальная проекции точки А – А1 и А2 лежат на одной линии проекционной связи, перпендикулярной оси х.

3. Образование и закон проекционной связи 3х картинного комплексного чертежа

Трёх картинный комплексный чертёжобразуется путём совмещения П1, П2 и П3 (горизонтальной, вертикальной и профильной плоскостей)

Законы проекционной связи:

1. Горизонтальная и фронтальная проекции точки А – А1 и А2 лежат на одной линии проекционной связи, перпендикулярной оси х.

2. Фронтальная и профильная проекции точки А – А2 и А3 лежат на одной линии проекционной связи, перпендикулярной оси z.

3. Горизонтальная и профильная проекции точки А – А1 и А3 лежат на одной линии проекционной связи, перпендикулярной оси у.

Тема 1. Прямая и плоскость в комплексном чертеже

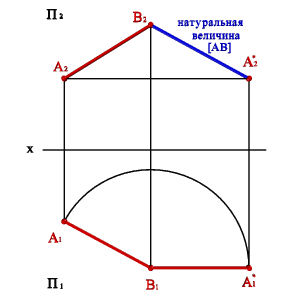
1. Способ прямоугольного треугольника, случаи применения.

Метод прямоугольного треугольника позволяет определить натуральную величину отрезка прямой общего положения и углов наклона его к плоскостям проекций. Натуральную величину отрезка определяют как гипотенузу прямоугольного треугольника, одним из катетов которого является горизонтальная (фронтальная) проекция отрезка, другим – разность координат концов отрезка до горизонтальной (фронтальной) плоскости проекций

2. Условия принадлежности прямой к плоскости

1. Прямая принадлежит плоскости, если две её точки принадлежат этой плоскости.

2. Прямая принадлежит плоскости, если имеет с плоскостью одну общую точку и параллельна какой-либо прямой, расположенной в этой плоскости.

3. Линии частного и общего положения

Прямая общего положения – прямая, наклоненная под произвольными углами ко всем трем плоскостям проекций

Прямые частного положения – линии уровня:

горизонталь (//П1) фронталь (//П2) профильная прямая (//П3)

(), (), ()

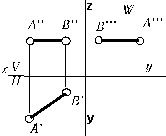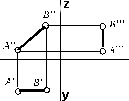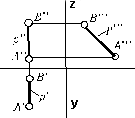и проецирующие прямые:

горизонтально-проецирующая фронтально-проецирующая

(), ()

профильно-проецирующая

4. Примеры прямых и плоскостей уровня, проецирующих прямых и плоскостей, свойства вырожденных проекций.

ПРОЕЦИРУЮЩИЕ ПЛОСКОСТИ (заданы вырожденными проекциями) 

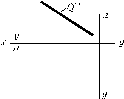
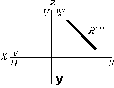
ПЛОСКОСТИ УРОВНЯ (заданы вырожденными проекциями) 

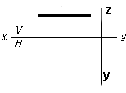
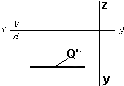
Вырожденная проекция прямой проецируется в точку, плоскость – в прямую, поверхность – в своё основание. Где бы на прямой не лежала принадлежащая ей точка, одна проекция точки совпадает с вырожденной проекцией прямой; где бы в плоскости не лежали принадлежащие ей точка или линия, одна проекция их принадлежит вырожденной проекции плоскости; где бы на поверхности не лежали принадлежащие ей точка или линия, одна проекция их принадлежит вырожденной в основание проекции поверхности или части её.

Тема 2. Преобразования комплексного чертежа

1. Способ замены плоскостей проекций

Сущность этого способа заключается в том, что заменяют одну из плоскостей на новую плоскость, расположенную под любым углом к ней, но перпендикулярную к незаменяемой плоскости проекции. Новая плоскость должна быть выбрана так, чтобы по отношению к ней геометрическая фигура занимала положение, обеспечивающее получение проекций, в наибольшей степени удовлетворяющих требованиям условий решаемой задачи. Для решения одних задач достаточно заменить одну плоскость, но, если это решение не обеспечивает требуемого расположения геометрической фигуры, можно провести замену двух плоскостей.

Применение этого способа характеризуется тем, что пространственное положение заданных элементов остается неизменным, а изменяется система плоскостей проекций, на которых строятся новые изображения геометрических образов. Дополнительные плоскости проекций вводятся таким образом, чтобы на них интересующие нас элементы изображались в удобном для конкретной задачи положений.

2. Основные способы преобразования комплексного чертежа

Способ замены плоскостей проекций.

1. Преобразовать чертеж прямой общего положения так, чтобы относительно новой плоскости проекций прямая общего положения заняла положение прямой уровня.

Новую проекцию прямой, отвечающей поставленной задаче, можно построить на новой плоскости проекций П4, расположив ее параллельно самой прямой и перпендикулярно одной из основных плоскостей проекций, т. е. от системы плоскостей П1_|_П2 перейти к системе П4 _|_ П1или П4 _|_ П2. На чертеже новая ось проекций должна быть параллельна одной из основных проекций прямой. На рис. 108 построено изображение прямой l (А, В) общего положения в системе плоскостей П1 _|_ П4, причем П4 || l. Новая проекция прямой дает истинную величину А4В4отрезка АВ (см. § 11) и позволяет определить наклон прямой к горизонтальной плоскости проекций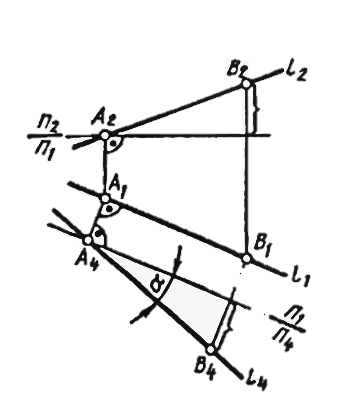 

1. Угол наклона прямой к фронтальной плоскости проекций (b = L₁П₂) можно определить, построив изображение прямой на другой дополнительной плоскости

1. Преобразовать чертеж прямой уровня так, чтобы относительно новой плоскости проекций она заняла проецирующее положение. Чтобы на новой плоскости проекций изображение прямой было точкой, новую плоскость проекций нужно расположить перпендикулярно данной прямой уровня. Горизонталь будет иметь своей проекцией точку на плоскости П4_|_ П1.( 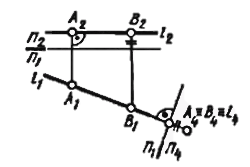), а фронталь f— на П4_|_ П2 Если требуется построить вырожденную в точку проекцию прямой общего положения, то для преобразования чертежа потребуется произвести две последовательные замены плоскостей проекций. На рис. 111 исходный чертеж прямой l (А,В) преобразован следующим образом: сначала построено изображение прямой на плоскости П4_|_ П2, расположенной параллельно самой прямой l. В системе плоскостей П2_|_ П4, прямая заняла положение линии l уровня (А2А4 _|_П2/П1; П2/П4 || l2).() Затем от системы П2 _|_ П4 осуществлен переход в систему П4 _|_П5, причем вторая новая плоскость проекций П5 перпендикулярна самой прямой l. Так как точки А и В прямой находятся на одинаковом расстоянии от плоскости П4, то на плоскости П5 получаем изображение прямой в виде точки (А5 = B5 = l5).

2. Преобразовать чертеж плоскости общего положения так, чтобы относительно новой плоскости она заняла проецирующее положение. Для решения этой задачи новую плоскость проекций нужно расположить перпендикулярно данной плоскости общего положения и перпендикулярно одной из основных плоскостей проекций. Это возможно сделать, если учесть, что направление ортогонального проецирования на новую плоскость проекций должно совпадать с направлением соответствующих линий уровня данной плоскости общего положения. Тогда все линии этого уровня на новой плоскости проекций изобразятся точками, которые и дадут «вырожденную» в прямую проекцию плоскости.

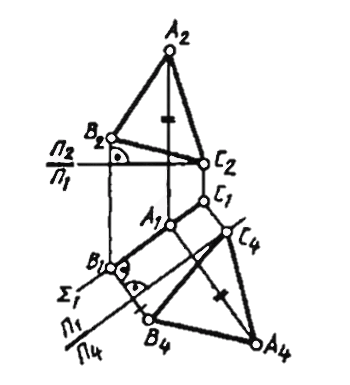
3. Преобразовать чертеж проецирующей плоскости так, чтобы относительно новой плоскости она заняла положение плоскости уровня. Решение этой задачи позволяет определить величину плоских фигур.

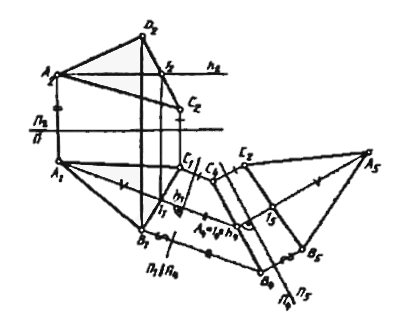
Способ плоскопараллельного движения

Плоскопараллельное перемещение треугольника ΔABC используемое для преобразования его ортогональных проекций, соответствующих плоскости общего положения δ, в проекции δ₂ // H для получения натуральной величины сторон и углов треугольника ΔABC требует выполнения следующих построений: - горизонтали (или фронтали) плоскости AD;

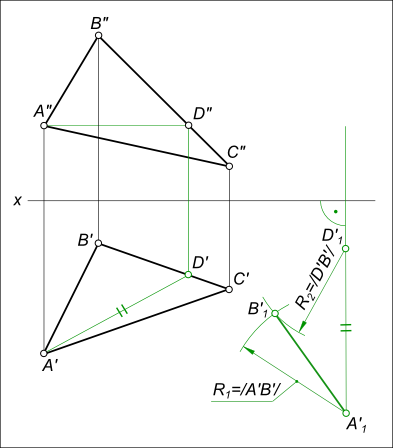
- перевода горизонтали плоскости в положение A₁D₁ ⊥ V: - на направлении перпендикуляра к плоскости V проведенном на свободном месте чертежа откладываем величину A`D` = A`<sub>1</sub>D`₁ - перестроение других точек проекции ΔA`B`C` на новое положение ΔA`₁B`<sub>1</sub>C`₁: - точку B`<sub>1</sub> дает пересечение дуг R<sub>1</sub> = /A`B`/ и R<sub>2</sub> = /D`B`/; - сторону B`D` продолжим до пересечения

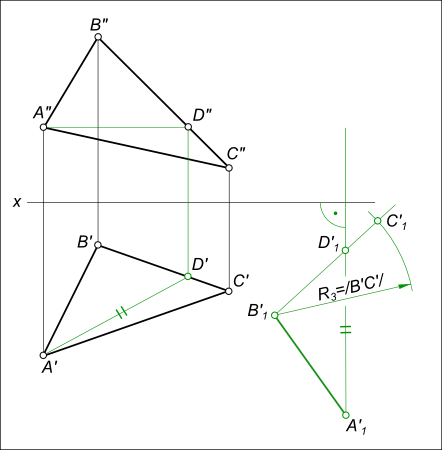
с дугой радиуса R₃ = /B`C`/; - проекции вершин треугольника в новом положении соединяем прямыми линиями;

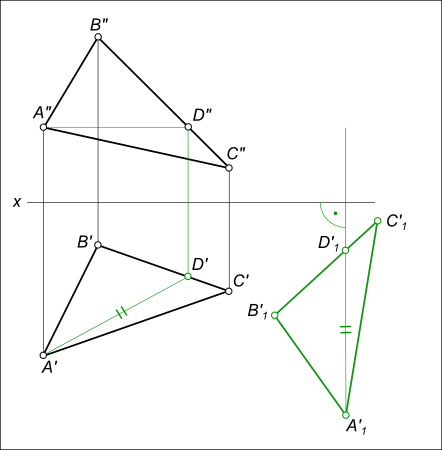
- перемещения фронтальных проекций ΔA"B"C" к новому положению ΔA"₁B"₁C"₁, происходящего в плоскостях уровня β1_V, β2_V и β3_V параллельных плоскости H;

- новое положение проекций определится на пересечении траекторий их движения в плоскостях уровня с вертикальными линиями проекционной связи; - перемещения фронтальной проекции ΔA"₁B"₁C"₁ в положение параллельное H,

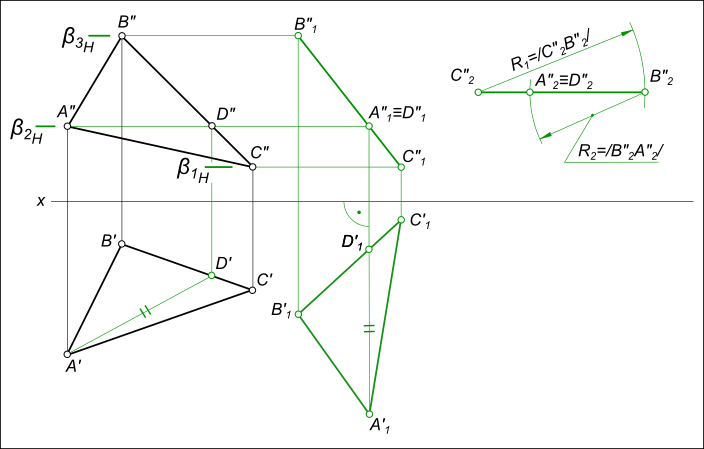
которое выполняем переводом прямой В"₁С"₁ - фронтальной проекции ΔA₁B₁C₁ в положение параллельное оси x: В"₂С"₂ // x; - перемещения горизонтальных проекций ΔA`<sub>1</sub>B`₁C`<sub>1</sub> к новому положению ΔA`₂B`<sub>2</sub>C`₂, происходящего в плоскостях уровня α1_H, α2_H и α3_H параллельных плоскости V;

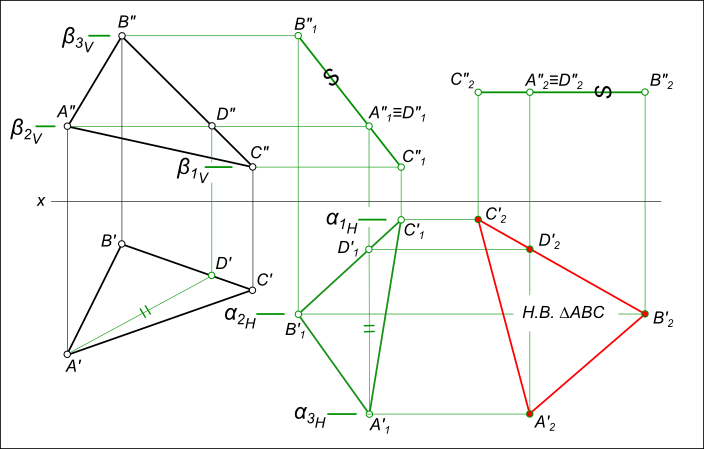
- новое положение проекций определится на пересечении траекторий их движения в плоскостях уровня с вертикальными линиями проекционной связи: проекция ΔA`<sub>2</sub>B`₂C`₂ соответствует натуральной величине треугольника ΔABC.

Способ вращения

Вращение вокруг оси, перпендикулярной плоскости проекции, является частным случаем параллельного перемещения. Отличие от параллельного перемещения состоит лишь в том, что за траекторию перемещения точки берется не произвольная линия, а дуга окружности, центр которой находится на оси вращения, а радиус равен расстоянию между точкой и осью вращения.