
10 Вопрос Общий порядок расчета переходных процессов классическим методом. Пример расчета.
Расет включает след. этап:
1)записб выражения для искомой переменной в виде:
X=Xпр+Xсв (*)
2) Нахождение принужденной составляющей общего решения на основании расчета установ. режима после коммутации цепи
3) Составление характеристического уравнения и определение его корней
Запись выражения свободной составляющей в форме определяемых типом найденных корней.
Подстановка полученных выражений принужден. и свободных составляющих в соответствии с (*).
Определяем НУ и на их основе постоянные интегрирования
Пример:



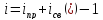

 следовательно
следовательно
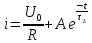 - 2
- 2

Переходные процессы при подключении последовательной R-L-C-цепи к источнику напряжения.

![]()
![]()
Тогда
для первого случая принужденная
составляющая этого напряжения![]()
|
Характеристическое
уравнение цепи
|
решая
которое, получаем
![]()
Для
апериодического характера переходного
процесса после подстановки (2) и (3) в
соотношение (1) можно записать
![]()
Для
нахождения постоянных интегрирования,
учитывая, что в общем случае
![]() и
в соответствии с первым законом
коммутации, запишем для t=0 два уравнения:
и
в соответствии с первым законом
коммутации, запишем для t=0 два уравнения:
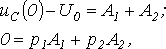
решая
которые, получим ,
,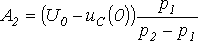
тогда

Тогда ток
в цепи

и напряжение
на катушке индуктивности

12Суть операторного метода расчета переходных процессов.
Сущность операторного
метода заключается в том, что функции
![]() вещественной
переменной t, которую называюторигиналом,
ставится в соответствие функция
вещественной
переменной t, которую называюторигиналом,
ставится в соответствие функция
![]() комплексной
переменной
комплексной
переменной![]() ,
которую называютизображением.
В результате
этого производные и интегралы от
оригиналов заменяются алгебраическими
функциями от соответствующих изображений
(дифференцирование заменяется умножением
на оператор р, а интегрирование –
делением на него). При решении этих
уравнений находятся изображения и далее
путем обратного перехода – оригиналы.
Важнейшим моментом при этом в практическом
плане является необходимость определения
только независимых начальных условий,
что существенно облегчает расчет
переходных процессов в цепях высокого
порядка по сравнению с классическим
методом.
,
которую называютизображением.
В результате
этого производные и интегралы от
оригиналов заменяются алгебраическими
функциями от соответствующих изображений
(дифференцирование заменяется умножением
на оператор р, а интегрирование –
делением на него). При решении этих
уравнений находятся изображения и далее
путем обратного перехода – оригиналы.
Важнейшим моментом при этом в практическом
плане является необходимость определения
только независимых начальных условий,
что существенно облегчает расчет
переходных процессов в цепях высокого
порядка по сравнению с классическим
методом.
13Преобразования Лапласа и его свойства.
Изображение
![]() заданной
функции
заданной
функции![]() определяется
в соответствии спрямым
преобразованием Лапласа:
определяется
в соответствии спрямым
преобразованием Лапласа:

|
Оригинал
|
А |
|
|
Изображение
|
|
|
|
|
В сокращенной записи соответствие между изображением и оригиналом обозначается, как:
![]() или
или
![]()
свойства изображений
Изображение суммы функций равно сумме изображений слагаемых:
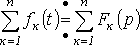 .
.
При умножении оригинала на коэффициент на тот же коэффициент умножается изображение:
![]() .
.
операторное сопротивление катушки индуктивности
![]()
![]() .
.
операторное сопротивление конденсатора
 =>
=> =>
=>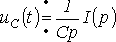
14Отыскание оригиналов. Теорема разложения.
Переход от изображения искомой величины к оригиналу может быть осуществлен следующими способами:
1. Посредством обратного преобразования Лапласа
 , запись сокращенно
, запись сокращенно
![]()
2. приминение формул сходства
в электротехике как правило пользуются теоремой разложения

то выражение может быть представлено в виде суммы простых дробей

Ак – неопределенный коэффициент
После математ. Преобразований, уравнение получает вид:

Воспользовавшись св. линейности, получим формулу разложения

15Законы Ома и Кирхгофа в операторной форме
Рис.

Уравнение, описывающе электромагнитные процессы в схеме после коммутации

Это же уравнение в области изображения

При нулевых начальных условиях
 ,
где
,
где
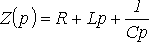 - операторное сопротивление.
- операторное сопротивление.
Получим 1-й закон Кирхгофа

Получим 2-й закон Кирхгофа

Правило замещения
L->Lp+Li(o)
C->(1/cp)+Uc(0)/p
i(t)->I(p)
e(t)->E(p)
16Порядок расчёта переходного процесса в разветвленной цепи операторным методом
Нахождение изобрадения скомой велечины
На данном этапе используется любой удобный метод расчета
I11(P)(r1+r2+Lp)-I22(P)(r2+Lp)=E(P)+Li2(0);
I22(P)(r2+Lp)+I22(P)(r2+Lp+1/cp)=Li2-Uc(0)/p;
I11(P)=([E/p+Li2(0)](r2+Lp+1/cp)-(r2+Lp)Li2(0)+Uc(0)/p))/(r1+r2+Lp)(r2+Lp+1/cp)-(r2+Lp)^2=I1(P)
I2(P), после проведения всех преоброзований получится в 3-й степени, т.к. льку схема 2-ого порядка, то будут еще 2 корня, соответствующие чисоу слагаемых в выражении лдя свободных состовляющих.
используем формуы разложения
а) F2(P)=0; p1=0;p2=…;p3=…;
б)находим производную F2’(P) и подставляем найденные корни в полученное выражение
F2’(P1)=r1+r2 ;F2’(P2)=….; F2’(P3)=…;
в) подставляем полученное значение в формулу разложения
f(t)=sum(k=1—3) F1(Pk)*e^Pkt/F2’(Pk)

