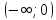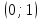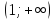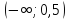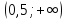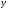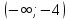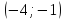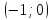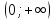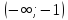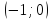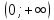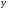ИПР_3 вариант 5

Министерство образования Республики Беларусь

 

Учреждение образования  «Белорусский государственный университет информатики и радиоэлектроники»

 

Факультет непрерывного и дистанционного обучения

 

Кафедра высшей математики

 

 

МАТЕМАТИКА, ЧАСТЬ 1

ИНДИВИДУАЛЬНАЯ ПРАКТИЧЕСКАЯ РАБОТА №1-3

«ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ ОДНОЙ ПЕРЕМЕННОЙ»

 

Вариант : 5

 

 

 

 

Минск 2017

Задача 1

Найдите производную функции.

1.05 y = sin(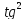(2x - 3)) + ch 2 +

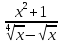
Решение

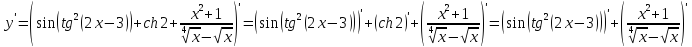
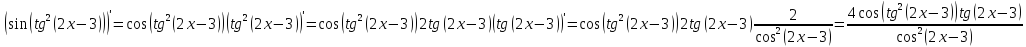
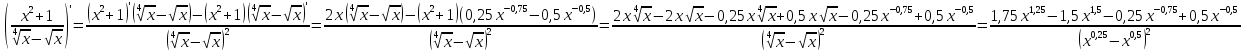
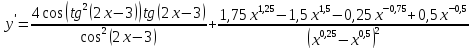
Задача 2

Найдите дифференциал заданной функции y = .

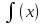Проверьте, удовлетворяет ли функция y = 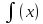 заданному уравнению.

2.05 y = x(cos2x – 1); x(y - 2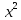sin 2x)dx - 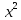dy = 0

Решение

По определению дифференциал функции равен

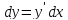
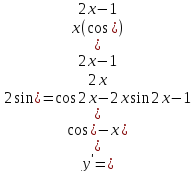
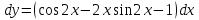
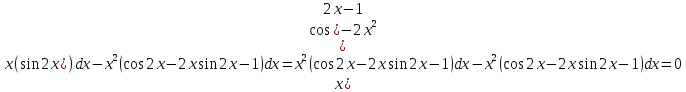
Задача 3

Найдите производную функции.

3.05 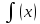= ( cos5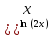

Решение

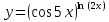
Прологарифмируем обе части:

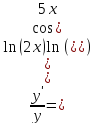
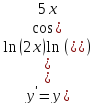
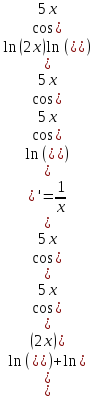
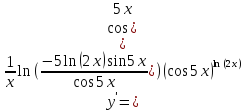
Задача 4

Найдите вторую производную 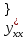 функции, заданной параметрически.

4.05

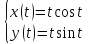
Решение

Функция задана в параметрическом виде.

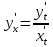
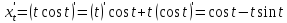
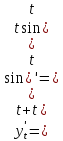
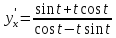
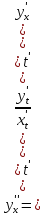
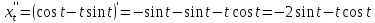
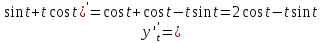
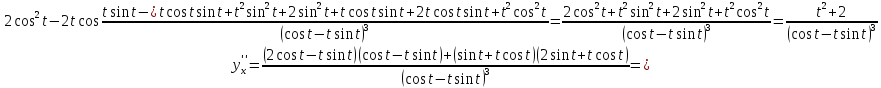
Задача 5

Заданы функция y = 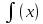 и точка . Найдите площадь треугольника, ограниченного осями координат и касательной, проведенной в точке 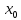.  к графику функции y = .

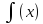5.05 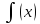= 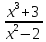; 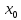= -1

Решение

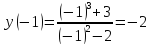
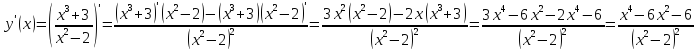
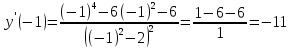
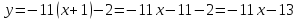
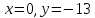
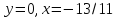
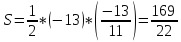
Задача 6

Найдите предел по правилу Лопиталя.

6.06

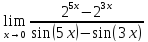
Решение

Правило Лопиталя позволяет раскрыть неопределенность вида 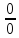или

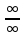
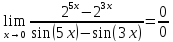
Применим правило Лопиталя, которое гласит, что предел отношения функций равен пределу отношения их производных:

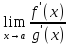
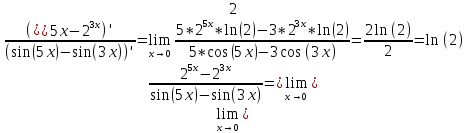
Задача 7

Разложите функцию по формуле Тейлора по степеням x -

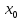
 до члена (x - 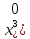включительно. Остаточный член запишите в форме Пеано.

7.05 y = 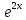; 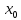= 1

Решение

Найдем значения функции и ее производных

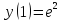
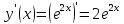
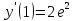
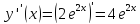
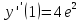
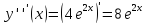
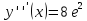
Подставляя полученные значения производных в формулу ряда Тейлора, получим:

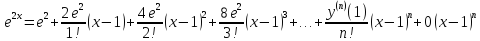
Задача 8

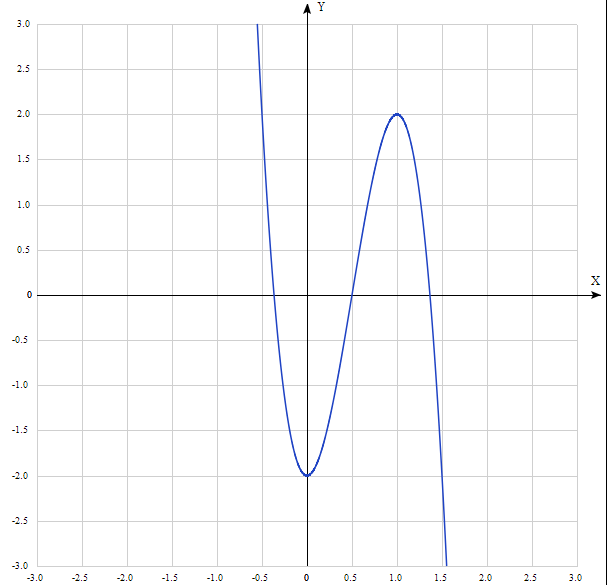
Методами дифференциального исчисления исследуйте функцию и постройте её график, используя результаты исследования.

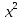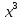8.05 y = 12 - 8 – 2

Решение

1. Область допустимых значений:

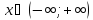
2. Проверим функцию на четность, нечетность. Функция 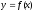называется четной (нечетной) если выполнены два условия:

Область определения симметрична относительно начала координат

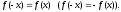
Если 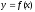четная, то график симметричен относительно оси ординат, а для нечетной – относительно начала координат.

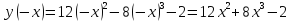
Функция не является ни четной, ни нечетной, т.е. общего вида.

Функция не является периодической

3. Найдем точки пересечения графика функции с осями координат

c осью ОY:

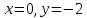
c осью ОX:

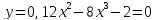
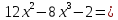
4. Найдем точки экстремума функции и промежутки монотонности

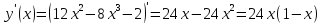
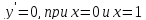
Составим таблицу

		0		1
	-	0	+	0	-
		-2		2
	убывает	min	возрастает	max	убывает

5. Найдем наклонные асимптоты 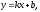где

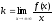
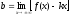
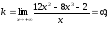
Поскольку коэффициент k равен бесконечности, наклонных асимптот не существует.

6. Найдем точки перегиба и промежутки выпуклости и вогнутости функции

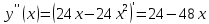
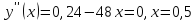
Составим таблицу

		0,5
	+	0	-
	вогнута	0	выпукла

Точка 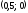- точка перегиба.

Задача 9

Методами дифференциального исчисления исследуйте функцию и постройте её график, используя результаты исследования.

9.05 y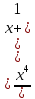

Решение

1. Область допустимых значений:

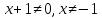
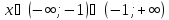
Т.к. 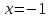- точка разрыва функции исследуем поведение функции в этой точке слева и справа

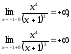
Т.к. пределы равны значит 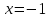точка разрыва второго рода.

Следовательно, прямая 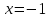- вертикальная асимптота.

2. Проверим функцию на четность, нечетность. Функция 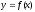называется четной (нечетной) если выполнены два условия:

Область определения симметрична относительно начала координат

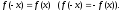
Если 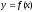четная, то график симметричен относительно оси ординат, а для нечетной – относительно начала координат.

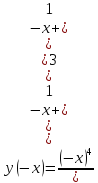
Функция не является ни четной, ни нечетной, т.е. общего вида.

Функция не является периодической

3. Найдем точки пересечения графика функции с осями координат

c осью ОY:

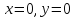
c осью ОX:

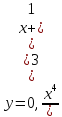
4. Найдем точки экстремума функции и промежутки монотонности

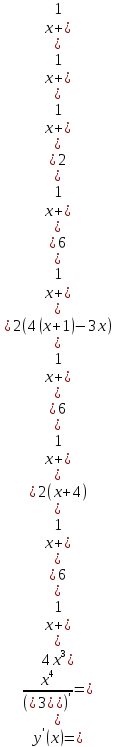
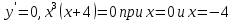
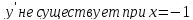
Составим таблицу

		-4		-1		0
	+	0	+	не сущ	-	0	+
		-9,5		не сущ		0
	возрастает	max	убывает		убывает	min	возрастает

5. Найдем наклонные асимптоты 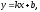где

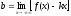
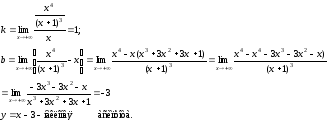
6. Найдем точки перегиба и промежутки выпуклости и вогнутости функции

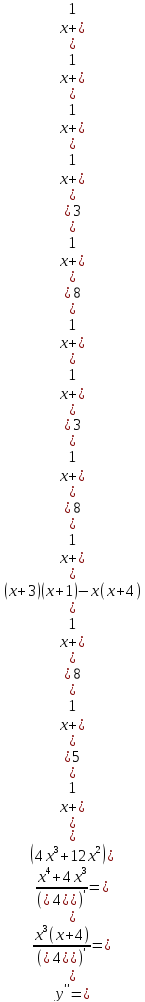
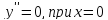
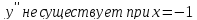
Составим таблицу

		-1		0
	-	не существует	+	0	+
	выпукла	не существует	вогнута	0	вогнута

Точка 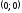- точка перегиба.

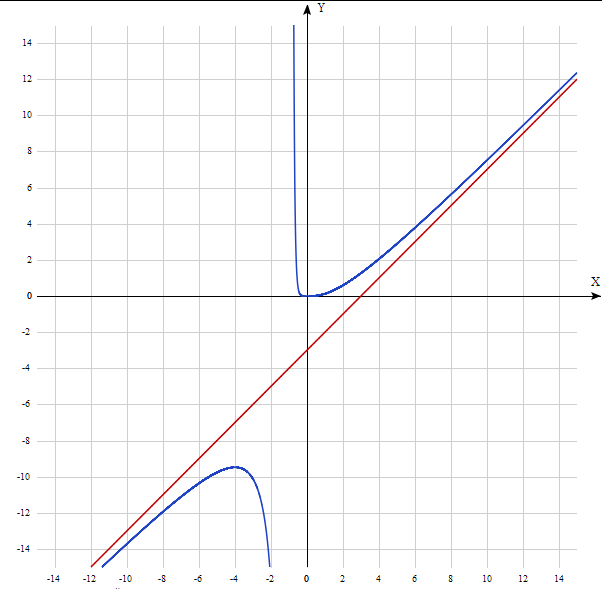
7. Построим график функции, используя результаты исследования.