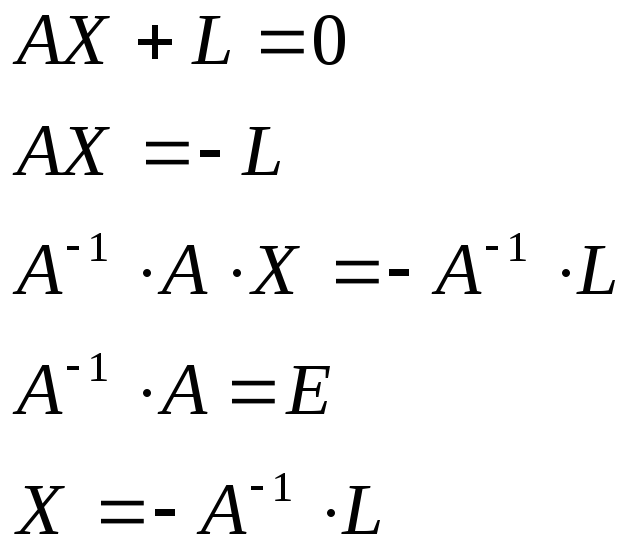ЭКТ-1 / Линейная алгебра

Линейная алгебра.

1.Векторы: действие с векторами. Компланарность векторов.

Вектор – направленный отрезок, имеющий определенную длину, одна точка которого называется началом, а другая концом.

Два вектора называются равными, если они имеют одинаковую длину и направление.

Единичным вектором называется вектор, длина которого равна 1.

Операции над векторами:

С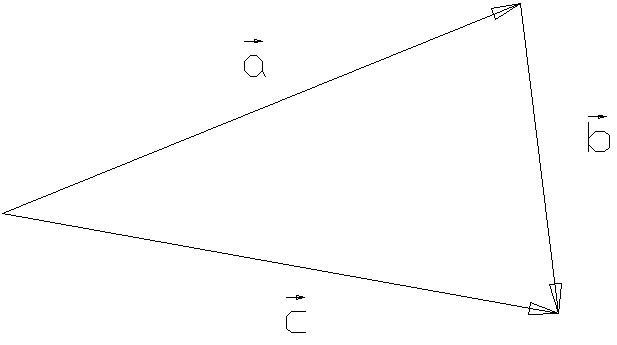умма векторов:

Р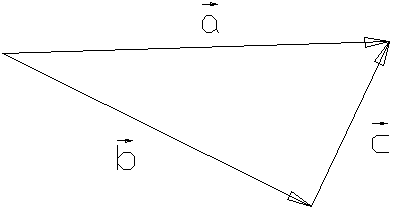азность векторов:

Умножение вектора на число:

если: – вектор сонаправлен с вектором ,

– векторы противоположно направлены.

Не линейные операции:

1.Скалярное произведение двух векторов:

2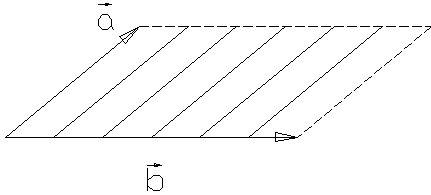.Векторное произведение:

Свойства вектора :

1. длина равна площади параллелограмма, т.е.

.

2) ; .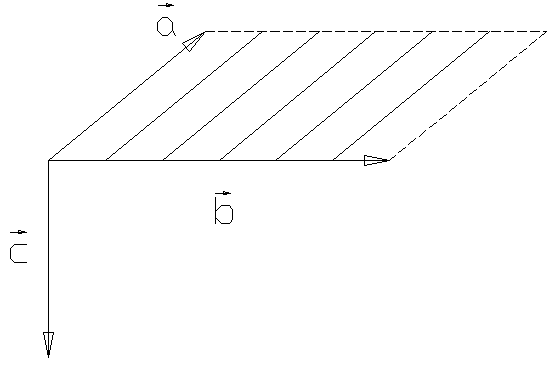

3) направление вектора должно быть таким, чтобы ближайший поворот от к был направлен против часовой стрелки.

3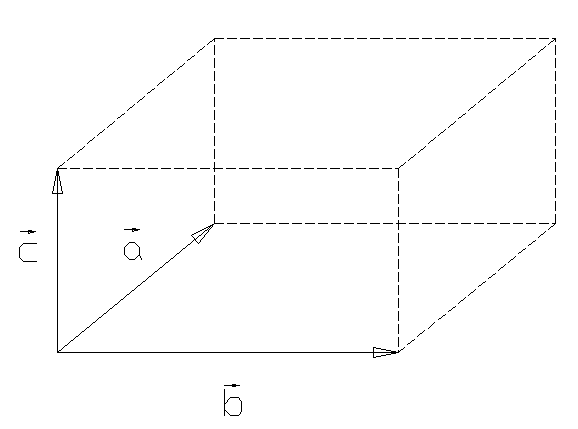. Смешанное произведение векторов:

.

Компланарность векторов:

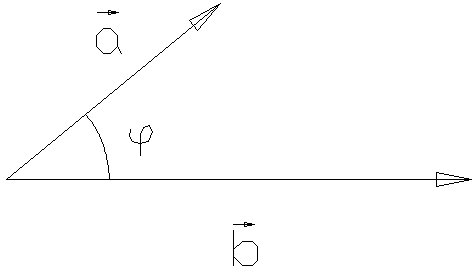
2.Скалярное произведение векторов.

Скалярное произведение двух векторов – это число равное произведению модулей этих векторов на косинус угла между ними, т.е.

Свойства:

1)

2)

3)

4)

Условие перпендикулярности двух векторов:

.

3. Векторное произведение векторов.

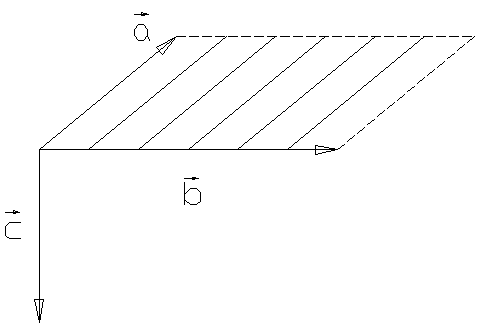
Векторное произведение – вектор, обладающий следующими свойствами:

1. длина равна площади параллелограмма, построенного на и ;

2. 

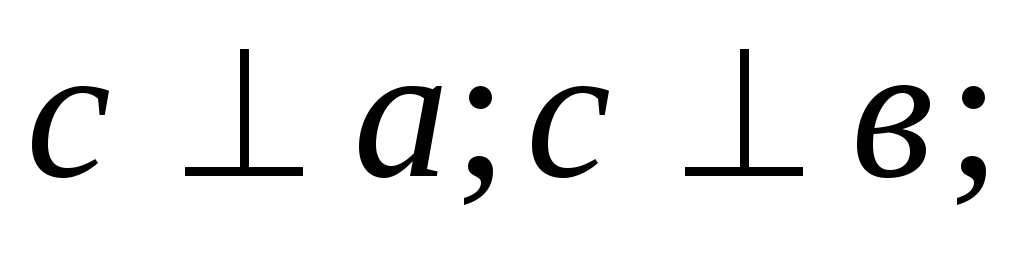
3. направление должно быть таким, что если смотреть с конца на и , то кротчайший поворот от к должен быть направлен против хода часовой стрелки.

Свойства векторного произведения:

1)

2)

3)

4) если , то или , тогда и – коллинеарны.

4. Смешанное произведение векторов

Смешанное произведение – число

1.

2. .

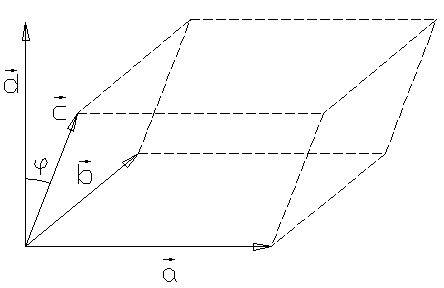
Смешанное произведение – число, абсолютная величина которого выражает объем параллелепипеда на векторах причем, со знаком «+», если обход от к происходит против часовой стрелки; со знаком «–», если обход осуществляется по ходу часовой стрелки.

Свойства смешанного произведения:

1) (по круговому принципу)

2) (если меняем попарно)

3) (вектора компланарны).

5. Неравенство Буняковского-Коши

6. Линейное уравнение. Однородная система

– линейное уравнение

– однородная система.

7. Матрицы: квадратная, диагональная, единичная, нулевая

Матрица размера – прямоугольная таблица чисел, расположенных в определенном порядке: в – строках и – столбцах.

1) – квадратная матрица;

2) Квадратная матрица , у которой все диагональные элементы равны 1, а остальные равны 0, называется единичной.

3) Нулевая матрица – матрица, все элементы которой равны 0.

,

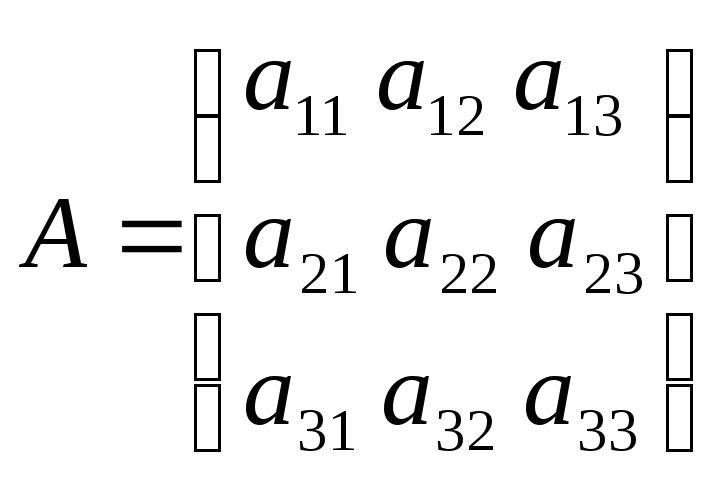где – главная диагональ.

Диагональная матрица:

.

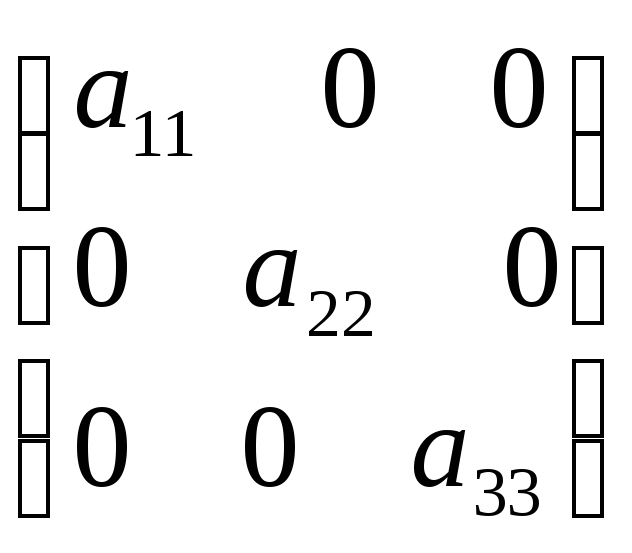8. Транспонирование, сложение матриц, производная

1. Транспонирование: 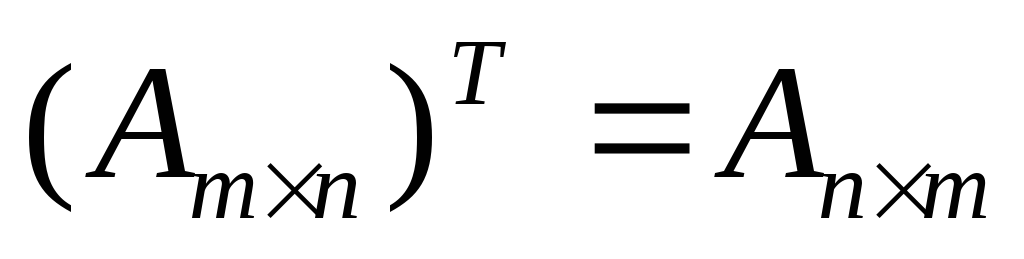– меняем местами столбцы и строки.

2. Сложение матриц:

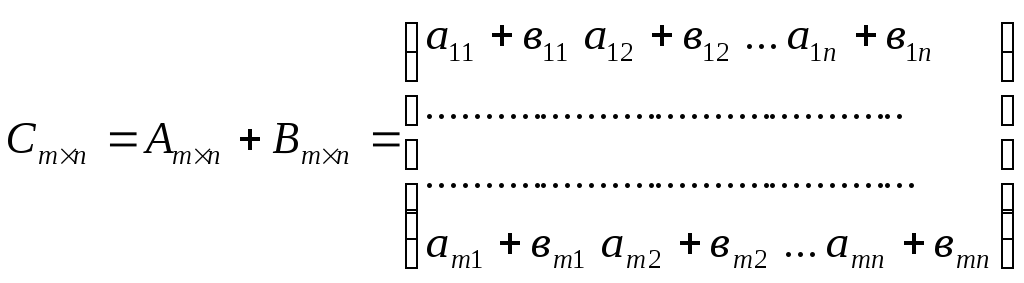
3.Производная матрица:

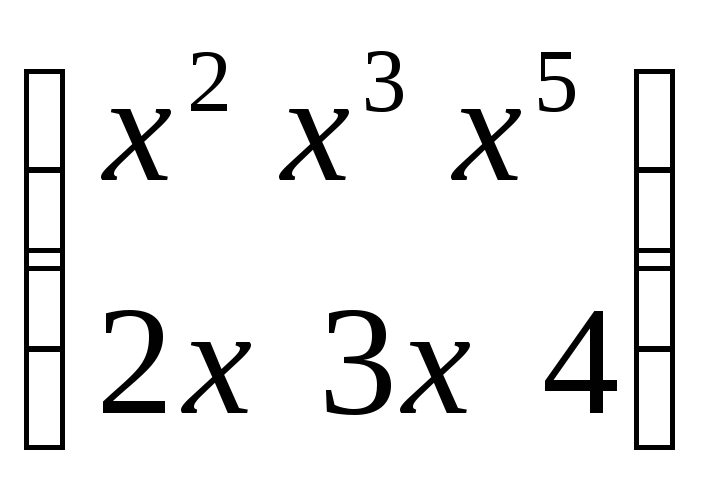– исходная

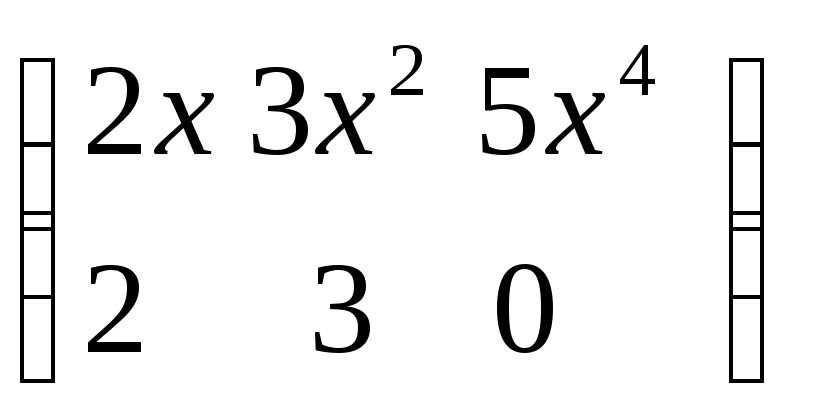– производная.

9.Законы умножения матриц

а)

б)

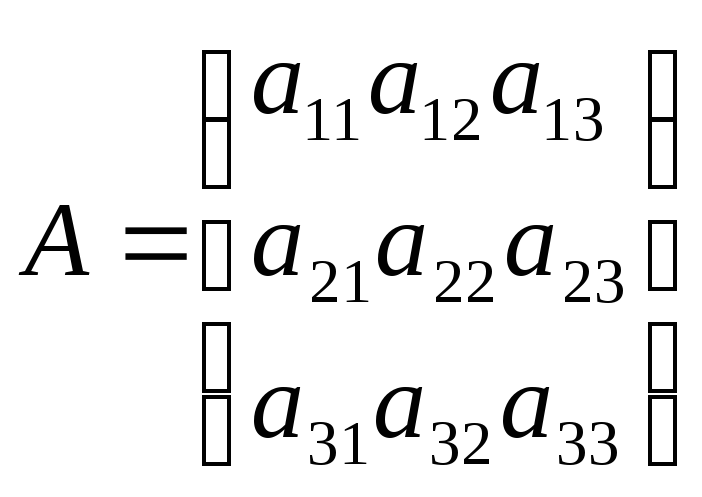
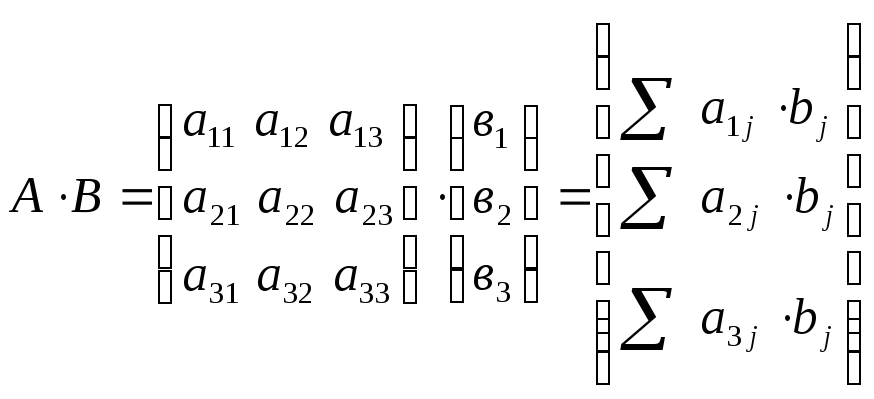
в)

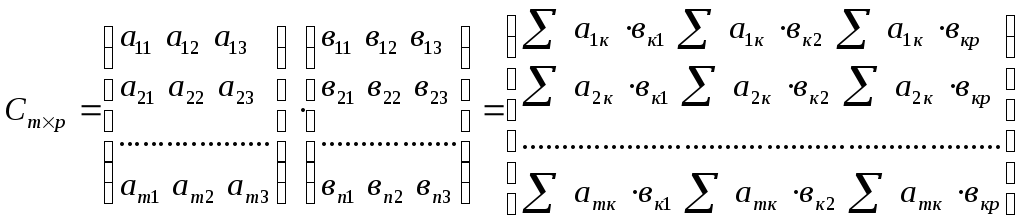
10.Определитель матрицы. Алгебраическое дополнение. След матрицы

Определитель матрицы – число, подсчитанное по формуле:

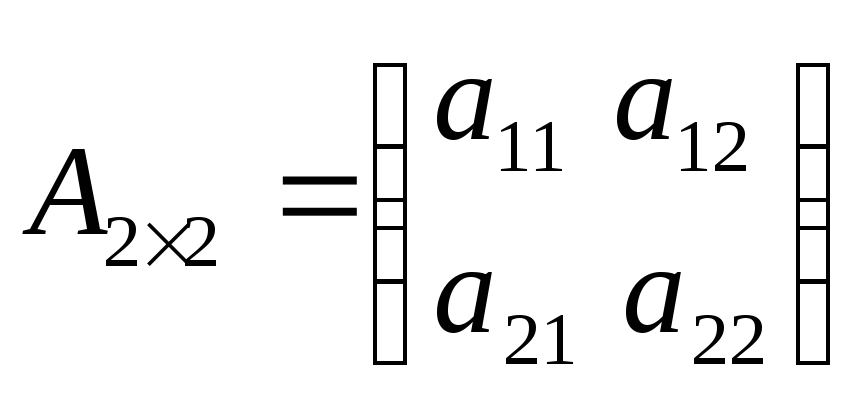
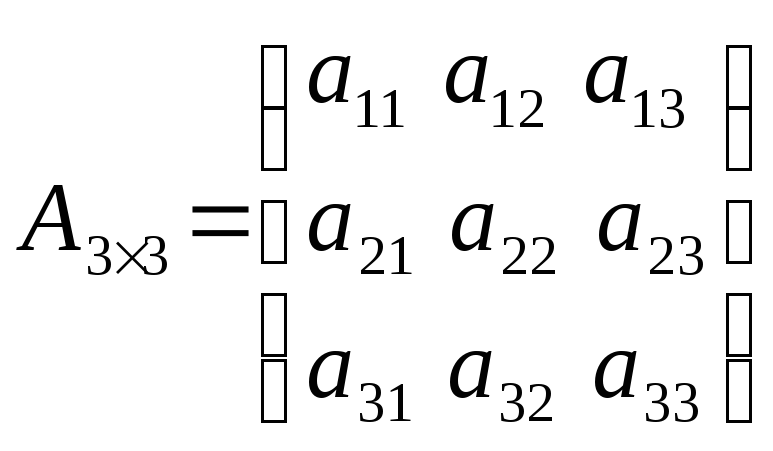
Алгебраическое дополнение элемента Аik – определитель, равный минору, взятый со знаком .

Минор:

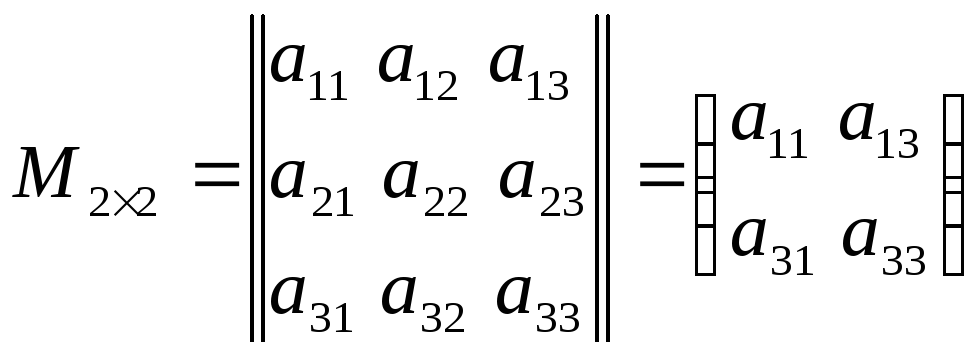
След матрицы

11. Неособенная матрица, обратная, симметричная, ортогональная

Неособенная матрица – нормальная матрица, у которой определитель не равен «0».

Обратной называется такая матрица , для которой , где Е – единичная матрица.

Симметричная: .

Ортогональная – такая квадратная матрица А, для которой: .

12. Ранг матрицы. Ранг произведения матрицы

Ранг матрицы – это число линейно независимых строк или столбцов.

– ранг матрицы

Каждый столбец или строка – вектор.

Например:

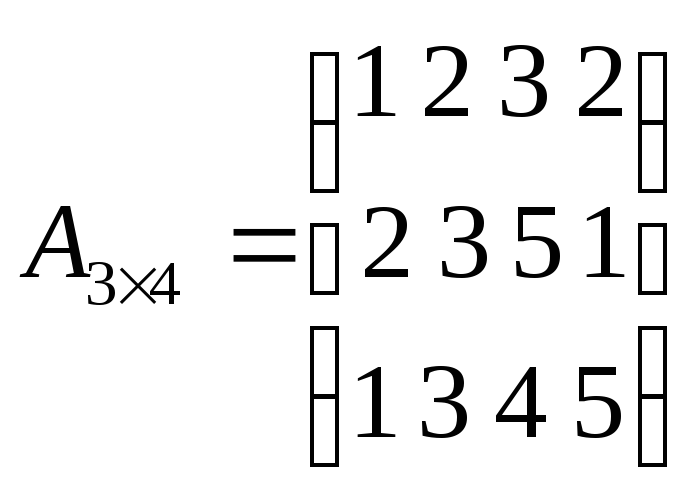
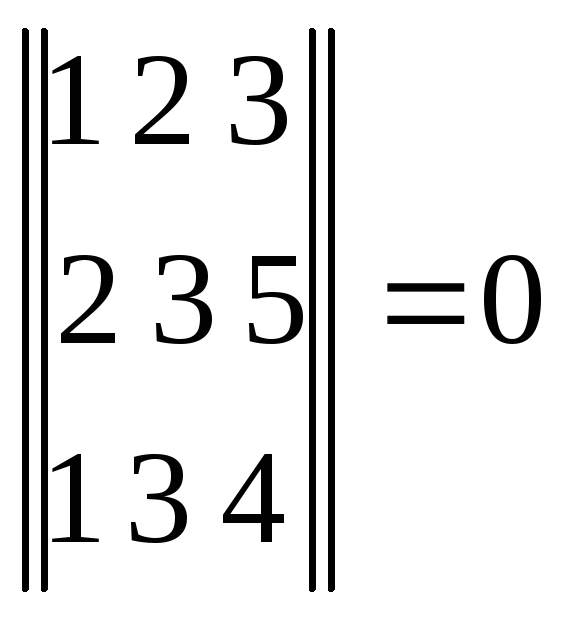
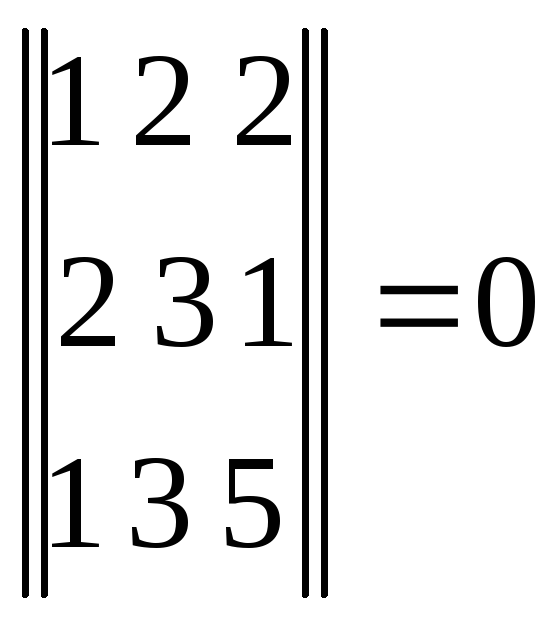
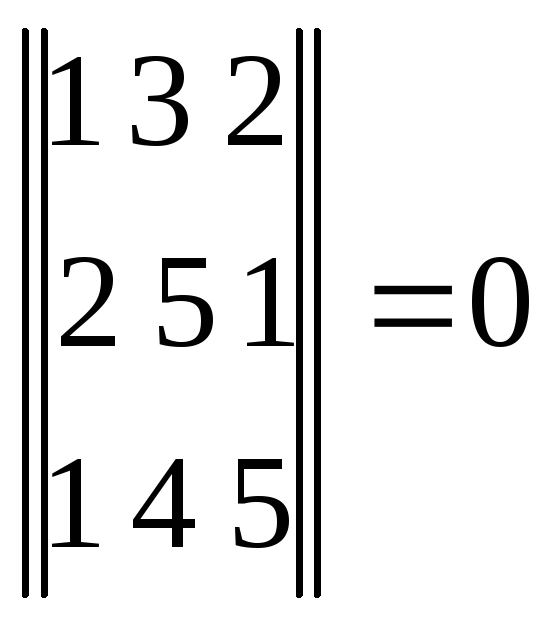
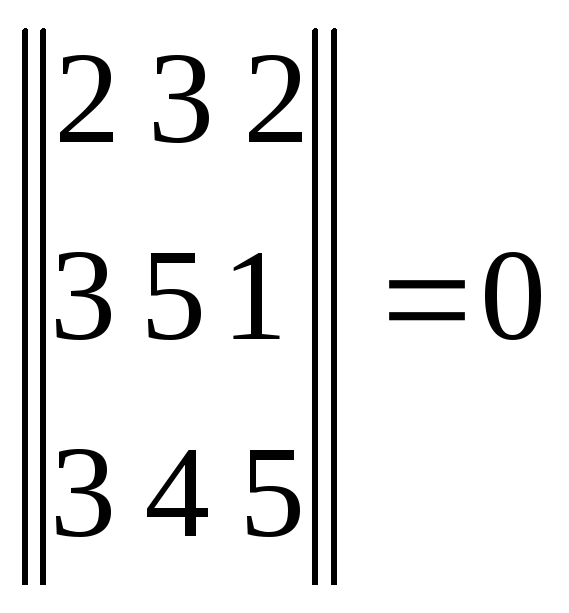
Элемент преобразования не меняет ранга матрицы.

Например: , тогда

.

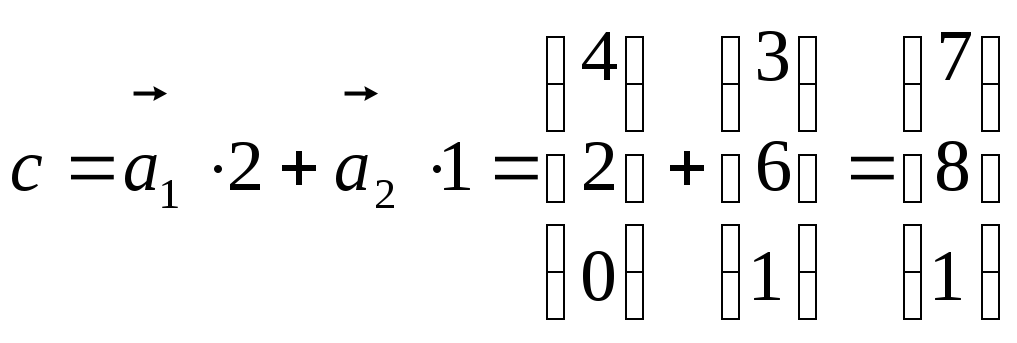
Ранг произведения матриц:

13.Квадратичные формы

1)

2) .

14. Решение систем линейных уравнений