ФР задачі (2)

5.1. Інвестор придбав дві акції до портфеля у співвідношенні 45 % та 55 %. Акції мають стандартне відхилення доходів 0,3 та 0,2 відповідно. Яким буде максимальне та мінімальне значення стандартного відхилення портфеля інвестора?

Дано:

х₁ = 0,45

х₂ = 0,55

σ₁ = 0,3

σ₂ = 0,2

Максимальний ризик портфеля, що складається з двох активів, буде при ρ = + 1

σ = х₁ σ₁+ х₂ σ₂ = 0,45*0,3+0,55*0,2 = 0,245

Мінімальний ризик портфеля, що складається з двох активів, буде при ρ = – 1:

σ = |х₁ σ₁- х₂ σ₂| = |0,45*0,3-0,55*0,2| = 0,025

Максимальне стандартне відхилення доходів портфеля (максимальний ризик портфеля) — 24,5 %, мінімальне стандартне відхилення доходів портфеля (мінімальний ризик) — 2,5 %.

5.2. Інвестор мав портфель, що складався з ризикових цінних паперів, стандартне відхилення якого дорівнювало 0,25 за очікуваного доходу 0,3. Безризикова ставка становить 12 %. Інвестор прийняв рішення змінити структуру портфеля, який на 50 % буде сформовано з ризикових інвестицій та на 50 % — з безризикових. Визначте стандартне відхилення та очікуваний дохід нового портфеля.

Дано:

σ₁ = 0,25

r₁ = 0,3

r₂ = 0,12

σ₂ = 0

х₁ = 0,50

х₂ = 0,50

σ_p = 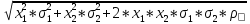= = 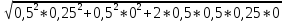0,125 = 12,5%

r_p = x₁*r₁ + x₂*r₂ = 0,5*0,3 + 0,5*0,12 = 0,21 = 21%

5.3. Інвестор має портфель, що складається з двох цінних паперів, які взяті у таких частках і мають таку очікувану дохідність та ризик:

ЦП	Очікувана дох. % (r)	Станд. відх, % (σ)	Частка (x)
А	11	20	0,45
В	16	24	0,55

Визначте максимальне і мінімальне значення стандартного відхилення доходів портфеля та його очікувану дохідність.

Максимальний ризик портфеля, що складається з двох активів, буде при ρ = + 1

σ = х₁ σ₁+ х₂ σ₂ = 0,45*0,2+0,55*0,24 = 0,222

Мінімальний ризик портфеля, що складається з двох активів, буде при ρ = – 1:

σ = |х₁ σ₁- х₂ σ₂| = |0,45*0,2-0,55*0,24| = 0,042

Максимальне стандартне відхилення доходів портфеля (максимальний ризик портфеля) — 22,2 %, мінімальне стандартне відхилення доходів портфеля (мінімальний ризик) — 4,2 %.

r_p = x₁*r₁ + x₂*r₂ = 0,45*0,11 + 0,55*0,16 = 0,1375 = 13,75%

5.4. Інвестор має портфель, що складається з цінних паперів А. Стандартне відхилення портфеля дорівнює 0,2 за очікуваного доходу 18 %. Інвестор прийняв рішення змінити структуру портфеля, який на 35 % буде сформовано з цінних паперів А та на 65 % — з цінних паперів В, що мають очікувану дохідність 10 % та стандартне відхилення доходів 0,1. Коефіцієнт кореляції між доходами цінних паперів А та В дорівнює 0,5. Визначте стандартне відхилення та очікуваний дохід нового портфеля.

Дано:

σ_А = 0,2

r_А = 0,18

r_В = 0,1

σ_В = 0,1

х_А = 0,35

х_В = 0,65

ρ = 0,5

σ_p = 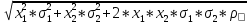= = 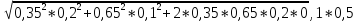0,125 = 11,69%

r_p = x₁*r₁ + x₂*r₂ = 0,35*0,18 + 0,65*0,1 = 0,128 = 12,8%

5.8. Безризикова ставка на ринку — 0,07; очікуваний дохід ринкового портфеля — 0,16; коефіцієнт  акції А дорівнює 1,2. Визначте очікувану дохідність акції. Побудуйте графік, дайте пояснення.

Дано:

R_f = 0,07

E(R_m) = 0,16

β = 1,2

Знайти:

E(R_i) - ?

лінії ринку цінних паперів

E(R_i) = R_f + β{E(R_m) - R_f}

E(R_i) = 0,07+1,2(0,16-0,07) = 0,173 = 17,3%

Лінія характеристики цінного папера графічно відтворює рів- няння регресії

R_i = a + βR_m

a = R_i - βR_m

a = 0,173 – 1,2*0,16 = -0,014

5.9. Очікується, що дохідність від інвестування коштів у акції Х може бути на рівні 18 %, ринкова премія становить 6 %, очікувана дохідність ринкового портфеля — 15 %. Визначте коефіцієнт  акції Х, побудуйте графік, дайте пояснення.

Дано:

{E(R_m) - R_f} = 0,06

E(R_m) = 0,15

E(R_i) = 0,18

β - ?

R_f = 0,15-0,06 = 0,09

лінії ринку цінних паперів

E(R_i) = R_f + β{E(R_m) - R_f}

β_i = =

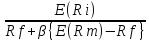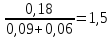
5.13. Безризикова ставка на ринку — 12 %; очікуваний дохід ринкового портфеля — 20 %. Кореляція доходів цінного папера з ринковим доходом — 0,6; стандартне відхилення доходів по цін- ному паперу — 0,30; стандартне відхилення доходів ринкового портфеля — 0,1. Визначте очікувану дохідність цінного папера. Побудуйте графік, дайте пояснення.

Дано:

R_f = 0,12

ρ = 0,6

E(R_m) = 0,2

σ_i = 0,3

σ_m = 0,1

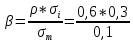= 1,8

лінії ринку цінних паперів

E(R_i) = R_f + β{E(R_m) - R_f}

E(R_i) = 0,12+1,8*(0,2-0,12) = 0,264