
Задание 8.
1.
Даны два вектора
![]() =и
=и
![]() .
Найти вектор
.
Найти вектор
![]() ,
если
,
если![]() Оz
Оz![]()
![]() ,
,![]() .
.
2.
Даны векторы
![]() =21,
=21,
![]() ;
0.
Найти вектор
;
0.
Найти вектор
![]() ,
если
,
если![]()
![]() ,
,![]()
![]() ,
,![]() .
.
3.
Даны векторы
![]() ={0;
2;1},
={0;
2;1},![]() ={1;
0; 2},
={1;
0; 2},![]() ={1;
1; 1}. Найти вектор
={1;
1; 1}. Найти вектор![]() ,
если
,
если![]()
![]() ,
,![]()
![]() ,
,![]()
![]() =3.
=3.
4.
Вектор
![]() ,
перпендикулярный к
,
перпендикулярный к![]() =
и
=
и
![]() =,
образует с осью Оу
тупой угол. Найти его координаты, зная,
что
=,
образует с осью Оу
тупой угол. Найти его координаты, зная,
что
![]() .
.
5.
Найти вектор
![]() ,
зная, что он перпендикулярен к
,
зная, что он перпендикулярен к![]() =2;
–3; 1
и
=2;
–3; 1
и
![]() =1,
–2, 3
и удовлетворяет условию
=1,
–2, 3
и удовлетворяет условию
![]() · {1; 2; –7} = 10.
· {1; 2; –7} = 10.
6.
Вектор
![]() ,
перпендикулярен к оси Оz
и вектору
,
перпендикулярен к оси Оz
и вектору
![]() =8;
–15; 3,
образует с осью Оx
острый угол,
=8;
–15; 3,
образует с осью Оx
острый угол, ![]()
= 51. Найти вектор
= 51. Найти вектор
![]() .
.
7.
Найти вектор
![]() ,
зная, что
,
зная, что![]() Оz,
Оz,
![]()
![]() ,
,![]()
=
= ![]() ,
где
,
где
![]() =–5;
3; –4.
=–5;
3; –4.
Найти вектор
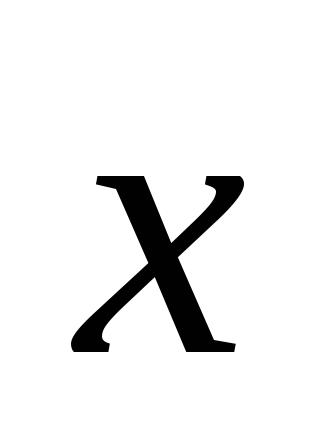 ,
зная, что
,
зная, что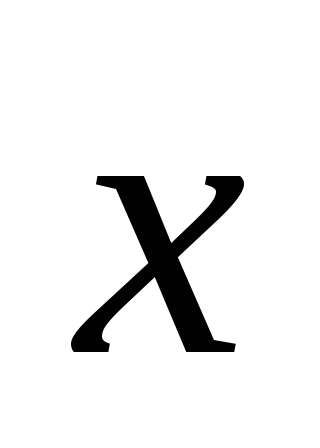
 ,
,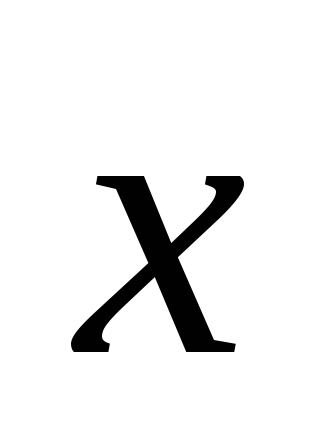
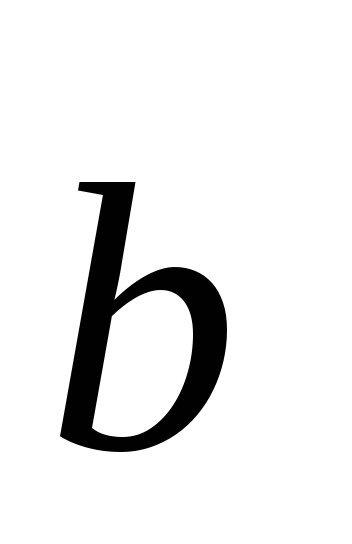 ,
,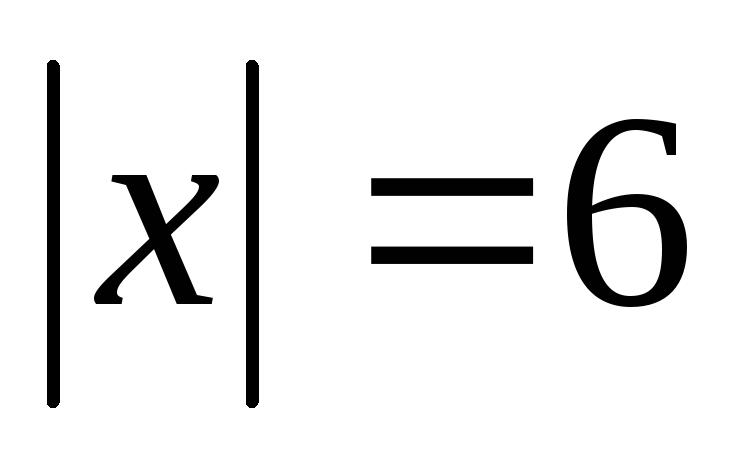 ,
где
,
где =2;
–3; –1,
=2;
–3; –1,
 =1;
6; –2.
=1;
6; –2.
Найти вектор
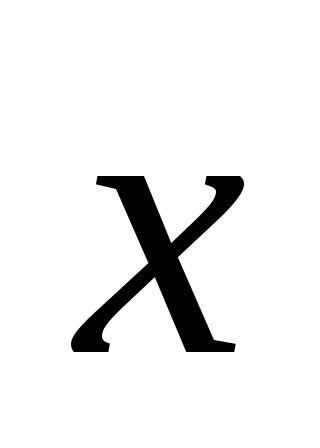 ,
зная, что
,
зная, что О,
О,
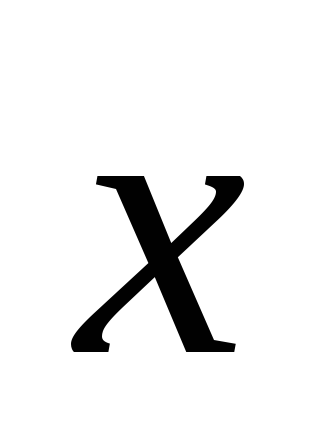
 ,
,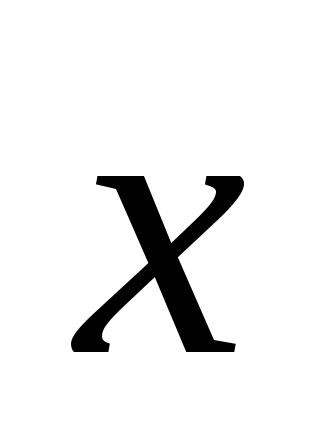
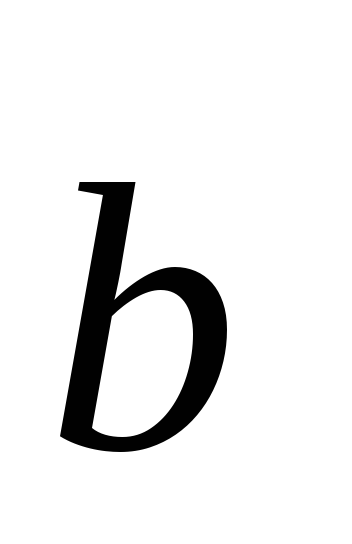 = 4, где
= 4, где =2;
–1; 1,
=2;
–1; 1,
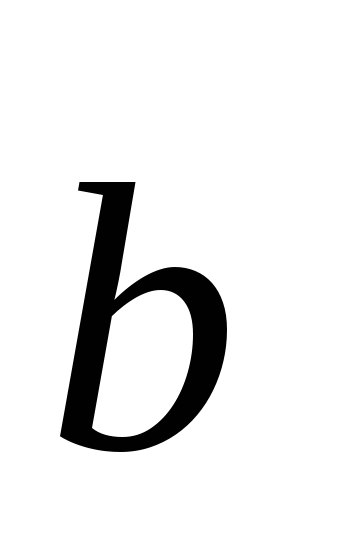 =1;
1; –1.
=1;
1; –1.
Найти вектор
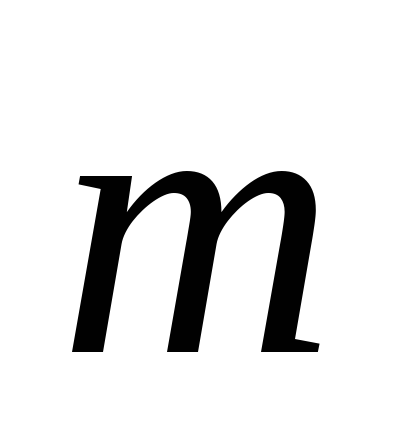 ,
зная, что
,
зная, что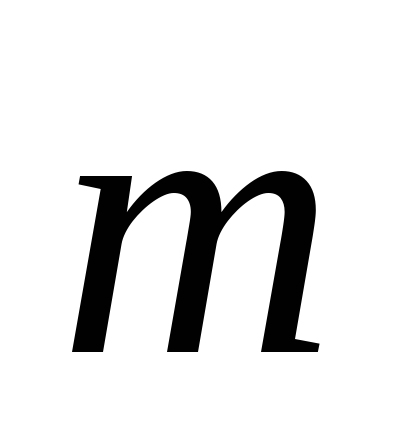
= 52,
= 52,
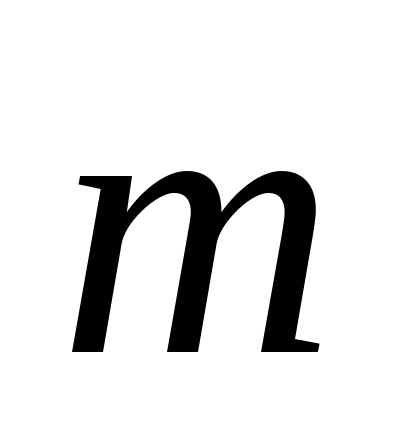 Оx,
Оx,
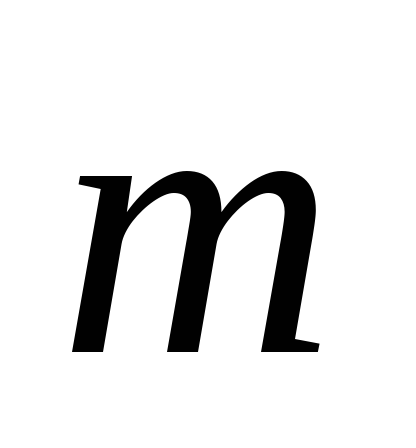
 и
и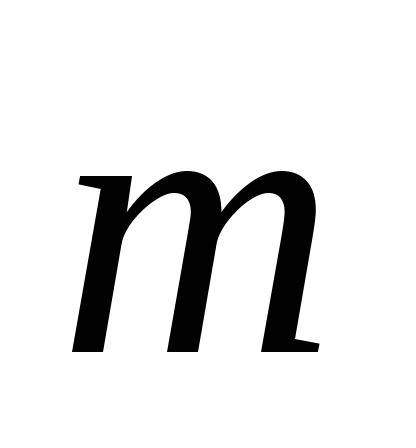 образует острый угол с осью Оy.
образует острый угол с осью Оy.
 =7;
–12; 5.
=7;
–12; 5.Найти вектор х, зная, что он перпендикулярен к векторам
 =0;
2; 1,
=0;
2; 1,
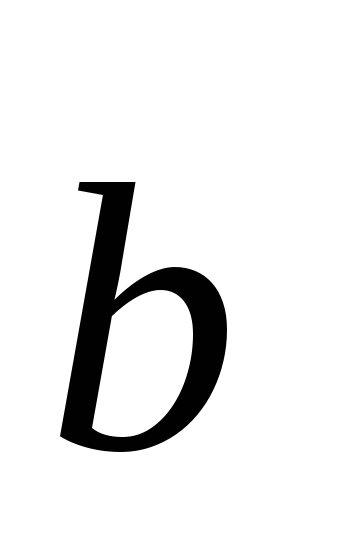 =1;
0; 2,
образует с осью Оy
тупой угол и
=1;
0; 2,
образует с осью Оy
тупой угол и
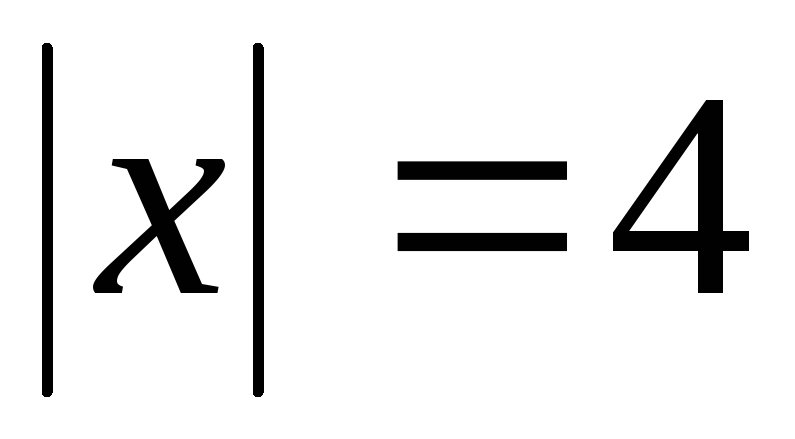 .
.Найти вектор
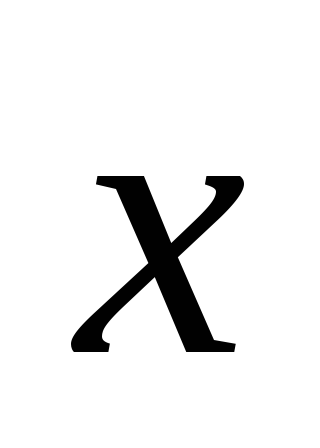 ,
если известно, что
,
если известно, что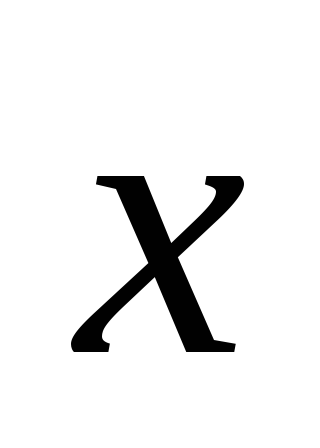
 ,
,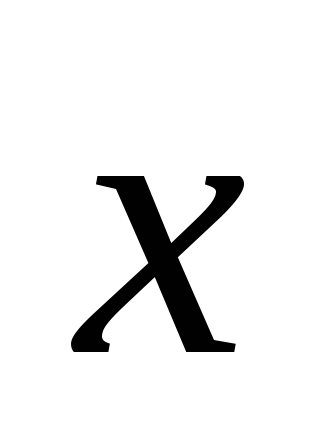
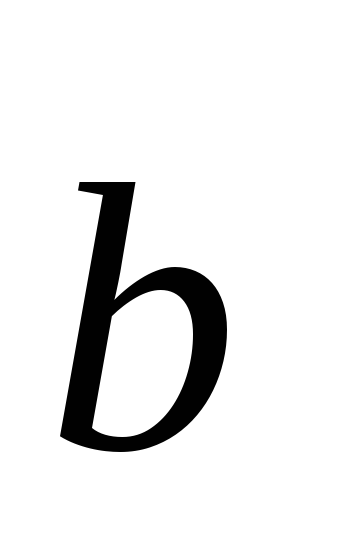 ,
,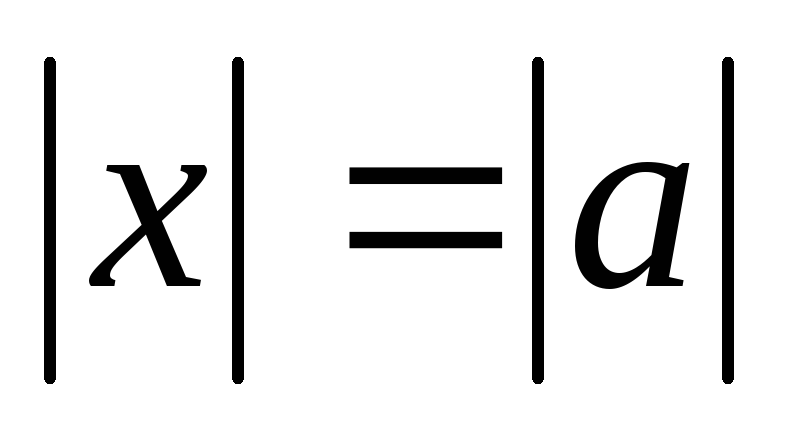 ,
, =2;
–1; 1,
=2;
–1; 1,
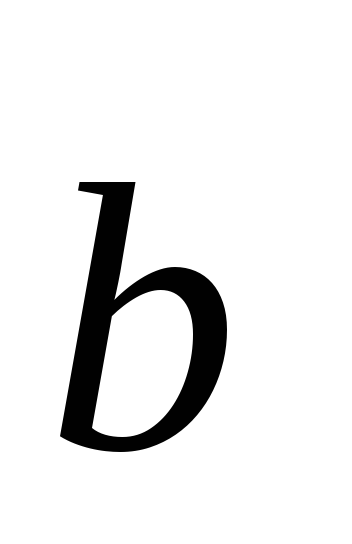 =1;
1; –1.
=1;
1; –1.Найти вектор
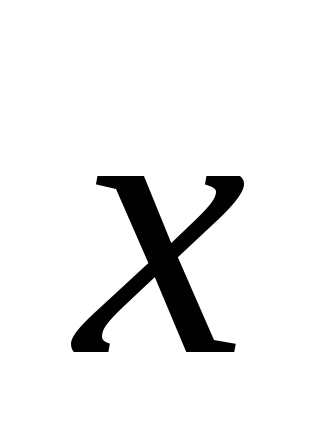 ,
зная, что он перпендикулярен векторам
,
зная, что он перпендикулярен векторам =2;
3; 1
и
=2;
3; 1
и
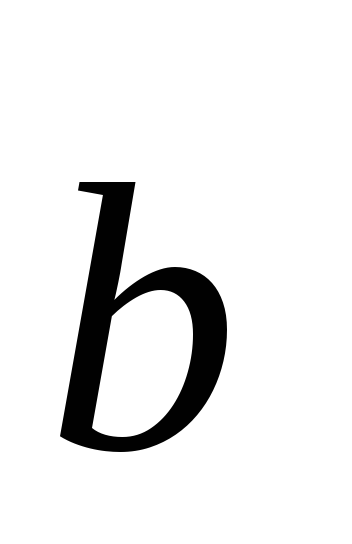 =1;
–2;3
и удовлетворяет условию
=1;
–2;3
и удовлетворяет условию
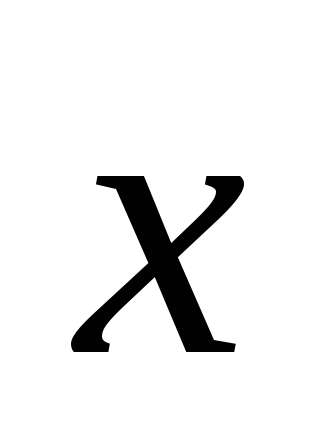 2;
–1; 1
= –6.
2;
–1; 1
= –6.Найти вектор
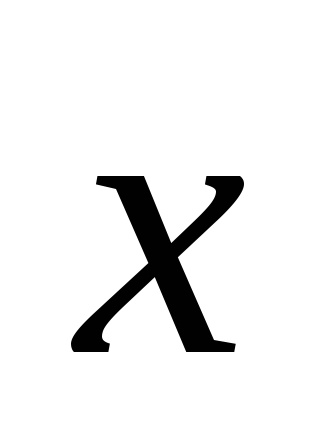 ,
перпендикулярен к векторам
,
перпендикулярен к векторам =4;
–2; –3
и
=4;
–2; –3
и
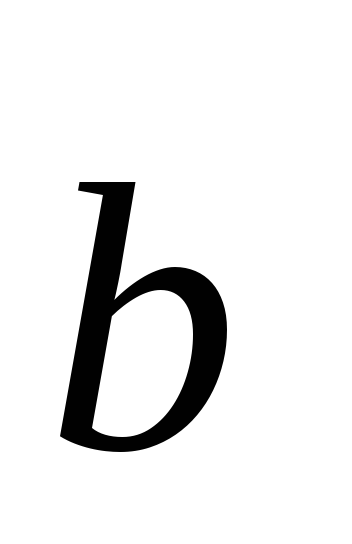 =0;
1; 3
и образующий с осью Оy
тупой угол,
=0;
1; 3
и образующий с осью Оy
тупой угол,
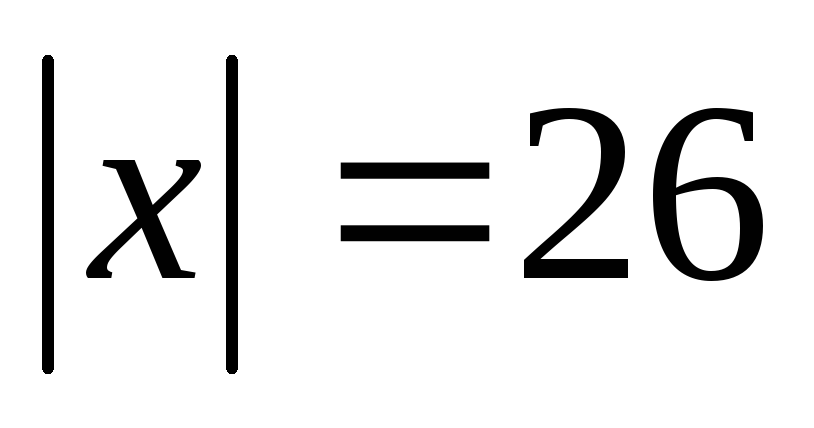 .
.Найти вектор
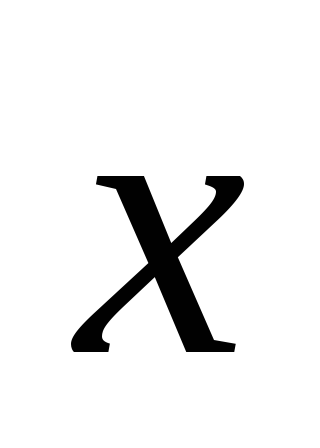 ,
зная, что он перпендикулярен векторам
,
зная, что он перпендикулярен векторам =4;
–6; 2,
=4;
–6; 2,
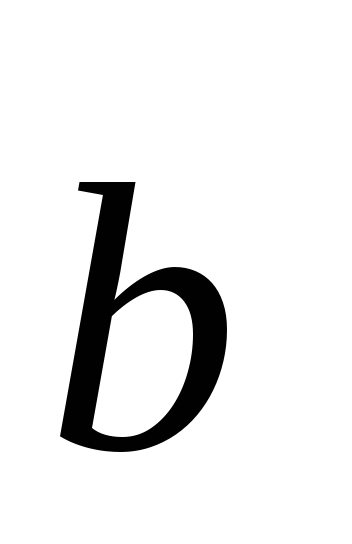 =1;
–2; 3
и удовлетворяет условию
=1;
–2; 3
и удовлетворяет условию
 .
.Найти вектор
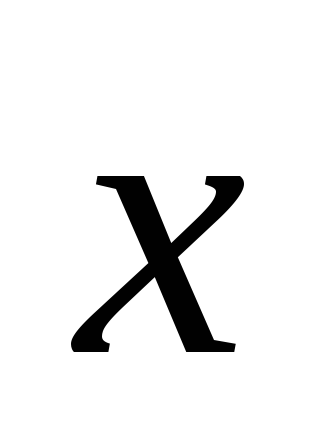 ,
зная, что
,
зная, что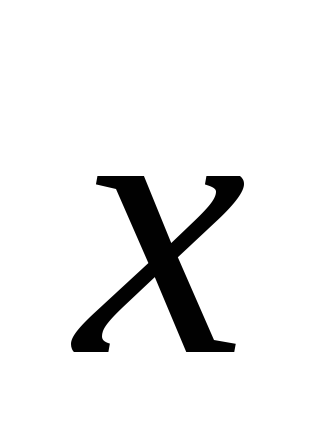 Оx,
Оx,

 ,
,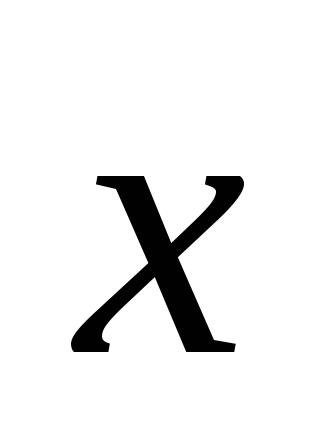
 =2,
где
=2,
где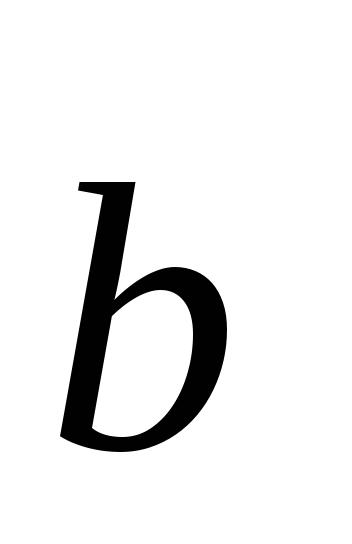 =6;
3; 1,
=6;
3; 1,
 =1;
1; 1.
=1;
1; 1.Найти вектор
 ,
зная, что
,
зная, что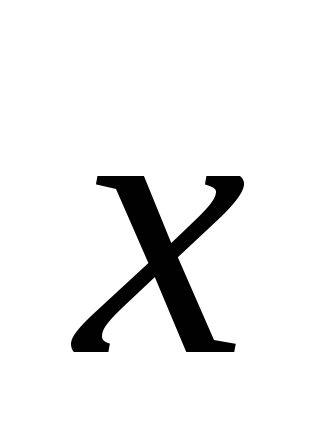
 ,
,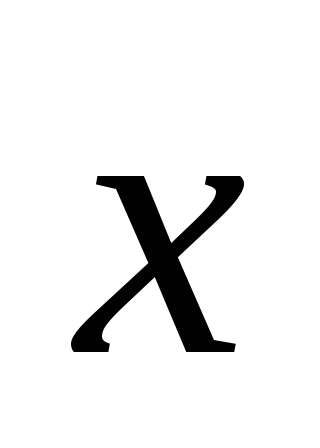
 ,
,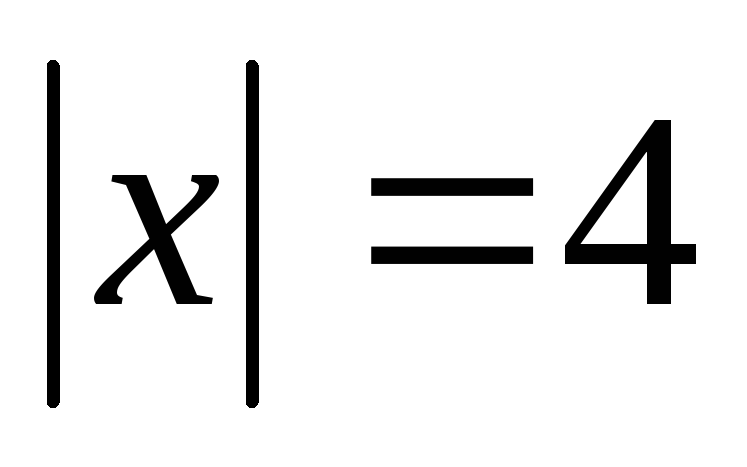 ,
если
,
если =2;
–1; 1,
=2;
–1; 1,
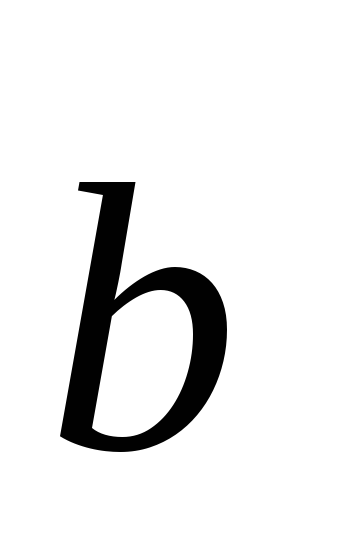 =0;
3;1.
=0;
3;1.Найти вектор
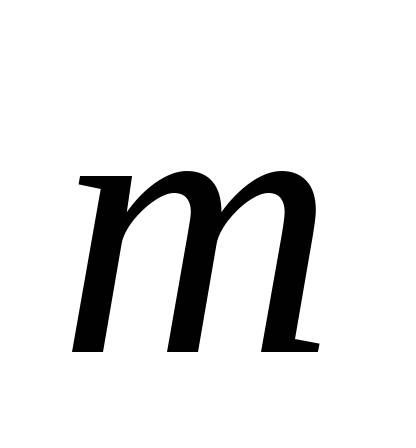 ,
зная, что он перпендикулярен к
,
зная, что он перпендикулярен к =2;
3; –1
и
=2;
3; –1
и
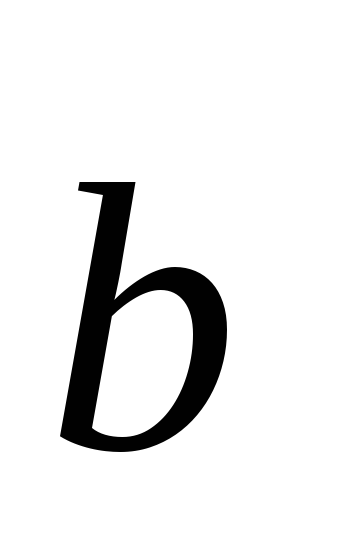 =1;
–2; 3
и удовлетворяет условию
=1;
–2; 3
и удовлетворяет условию
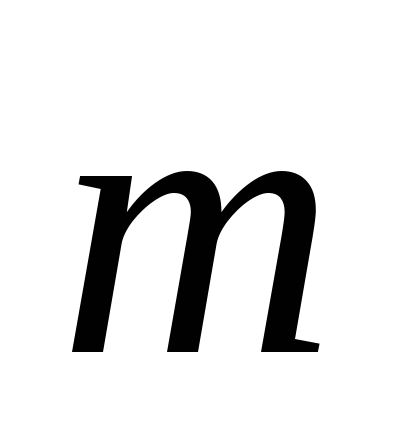
1; 1; 1
= –18.
1; 1; 1
= –18.Вектор
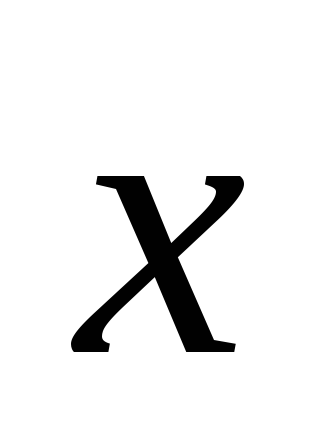 перпендикулярный к оси Оz
и вектору
перпендикулярный к оси Оz
и вектору
 =8;
–15; 3,
образует острый угол с осью Оx.
Найти
=8;
–15; 3,
образует острый угол с осью Оx.
Найти
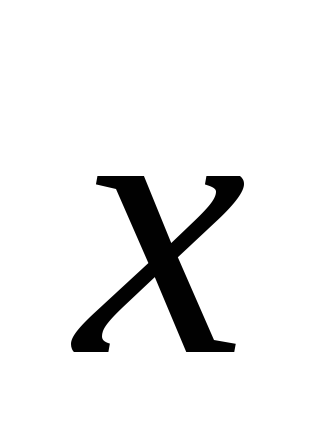 ,
если
,
если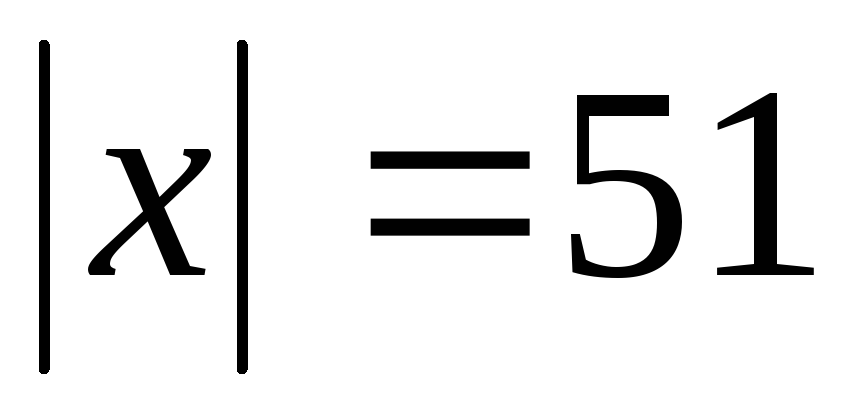 .
.Найти вектор
 ,
перпендикулярный к векторам
,
перпендикулярный к векторам =2;
3; –1
и
=2;
3; –1
и
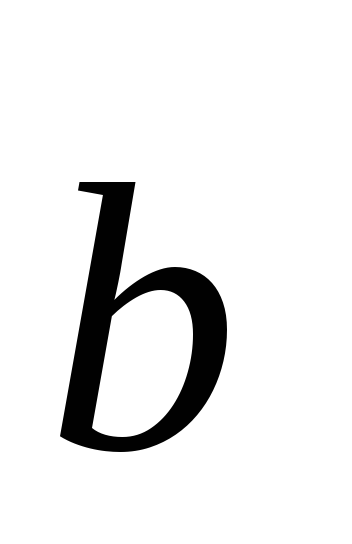 =1;
–2; 3
и удовлетворяющий условию
=1;
–2; 3
и удовлетворяющий условию
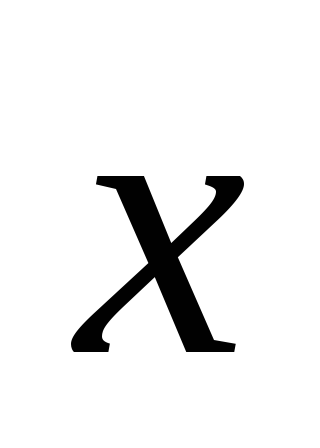
 =12,
где
=12,
где =2;
–1; 1.
=2;
–1; 1.Найти вектор
 ,
если известно, что
,
если известно, что
 ,
,
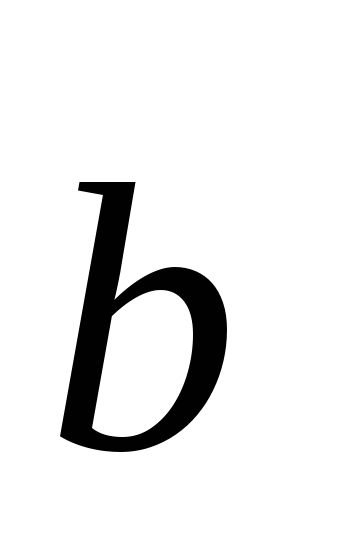 ,
, =1,
где
=1,
где
 =5;
7; 1,
=5;
7; 1,
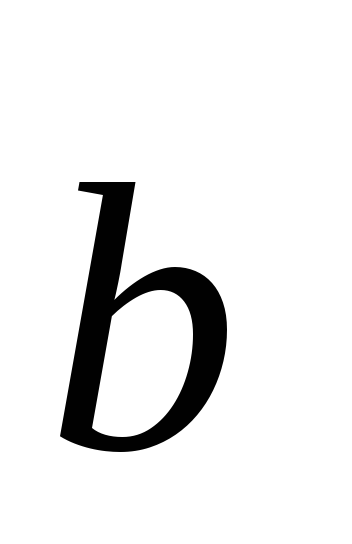 =4;
2; –1.
=4;
2; –1.Найти вектор
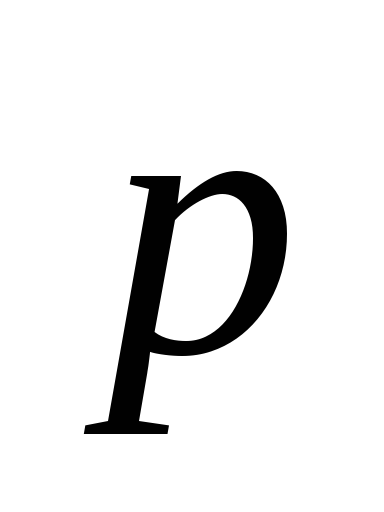 ,
зная, что
,
зная, что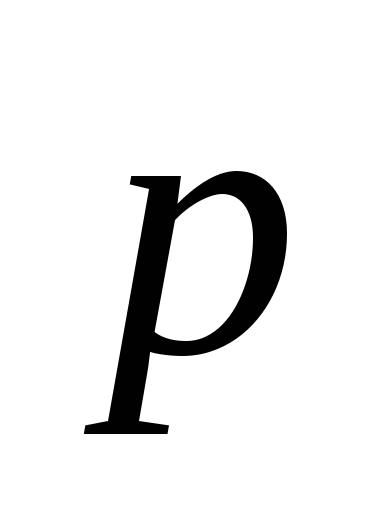 Оy,
Оy,
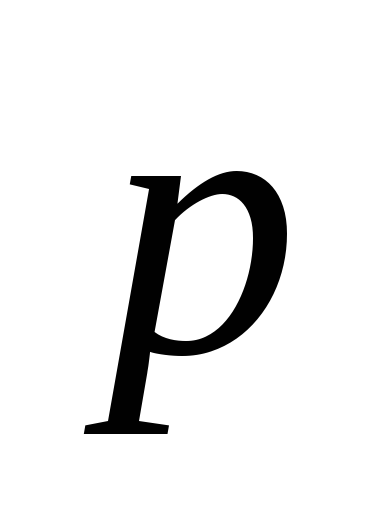
 ,
,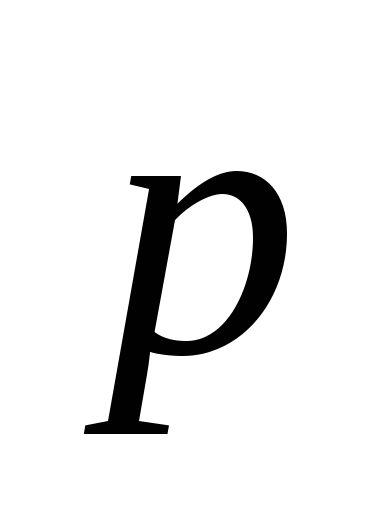
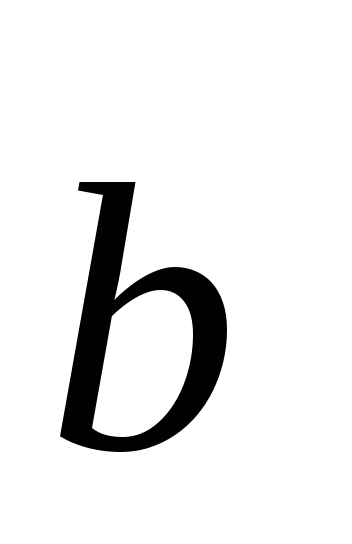 =–3,
где
=–3,
где =2;
3; –1,
=2;
3; –1,
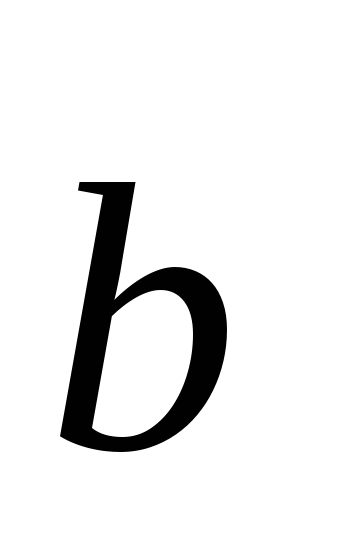 =1;
1; 1.
=1;
1; 1.Даны два вектора
 =2;–4;
3
и
=2;–4;
3
и
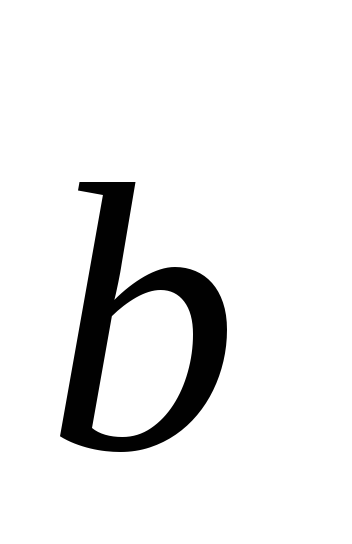 =–2;
3; 1.
Найти вектор
=–2;
3; 1.
Найти вектор
 ,
если
,
если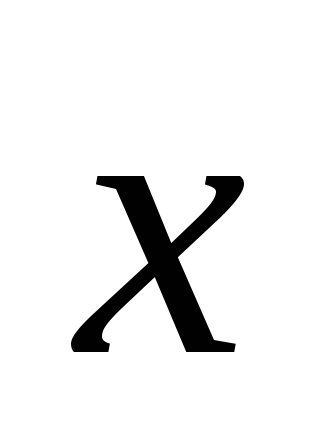 Оz,
Оz,
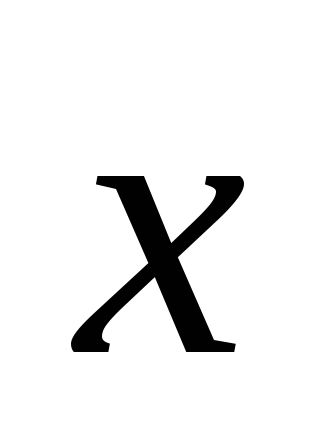
 ,
,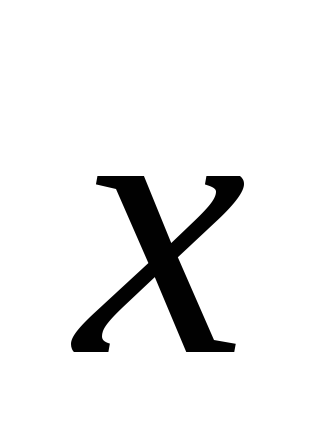
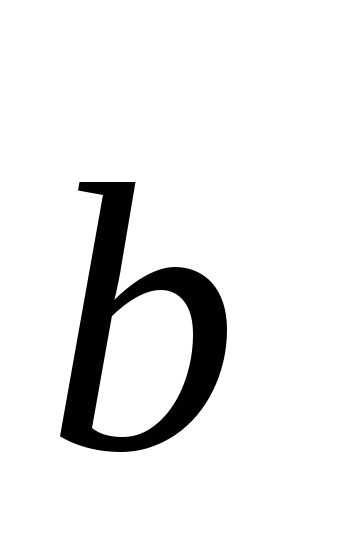 =6.
=6.Найти вектор
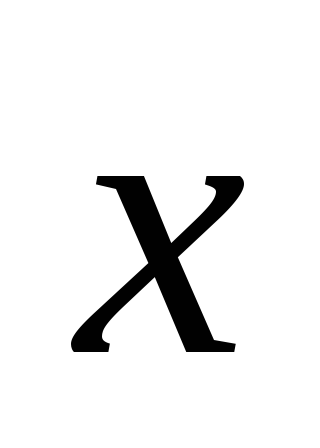 ,
зная, что
,
зная, что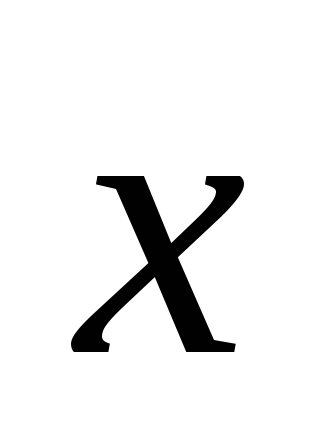
 ,
,
 ,
,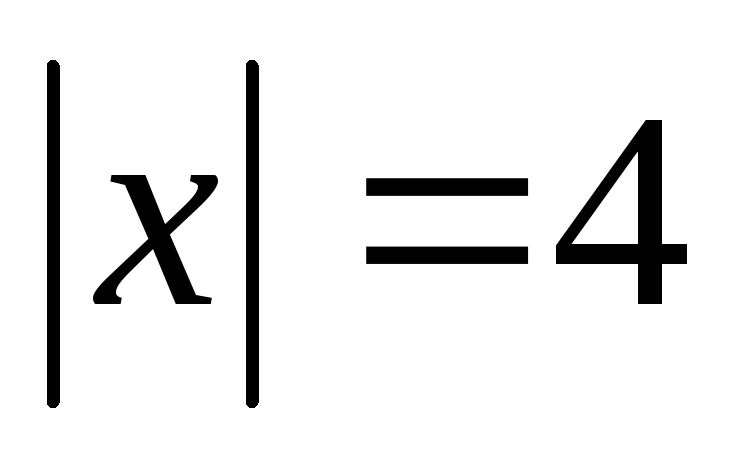 ,
где
,
где =3;
–2;1,
=3;
–2;1,
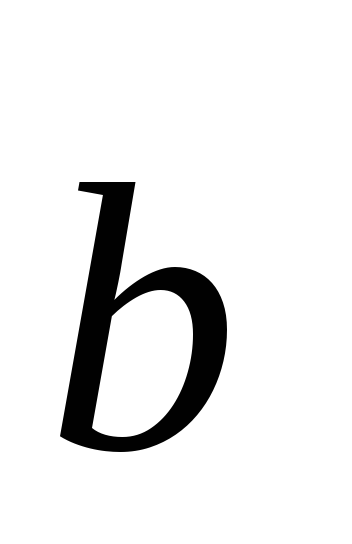 =4;
6; –1.
=4;
6; –1.Даны два вектора
 =1;
3; –5
и
=1;
3; –5
и
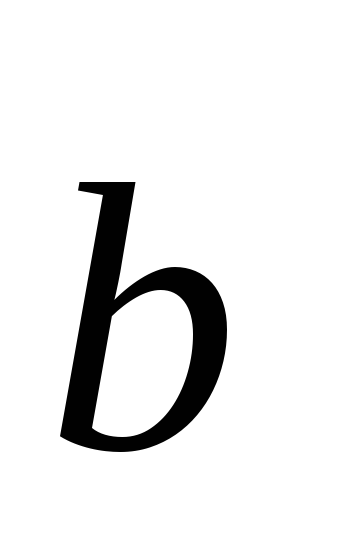 =–2;
1; 2.
Найти вектор с,
зная, что он перпендикулярен векторам
=–2;
1; 2.
Найти вектор с,
зная, что он перпендикулярен векторам
 и
и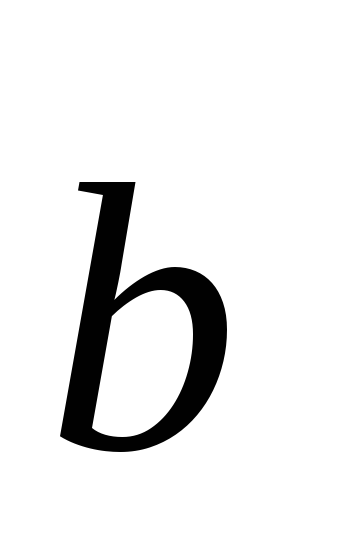 и удовлетворяет условию
и удовлетворяет условию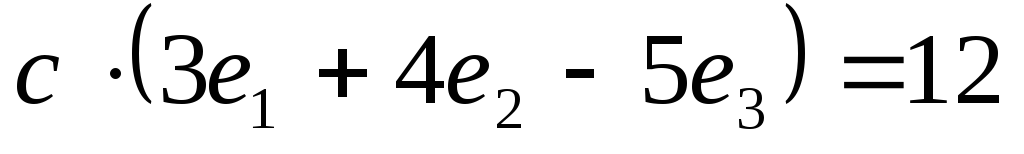 .
.Найти вектор
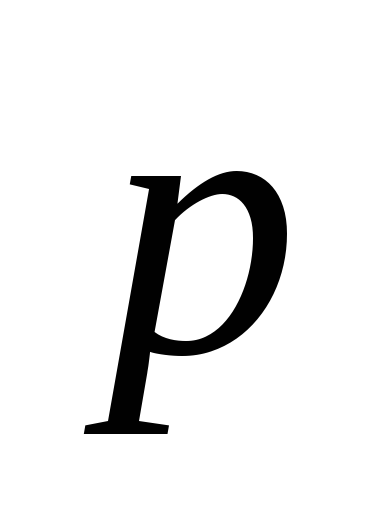 ,
зная, что он перпендикулярен к
,
зная, что он перпендикулярен к =2;
–1; 3
и
=2;
–1; 3
и
 =3;
–2; 1,
образует с осью Оx
острый угол,
=3;
–2; 1,
образует с осью Оx
острый угол, 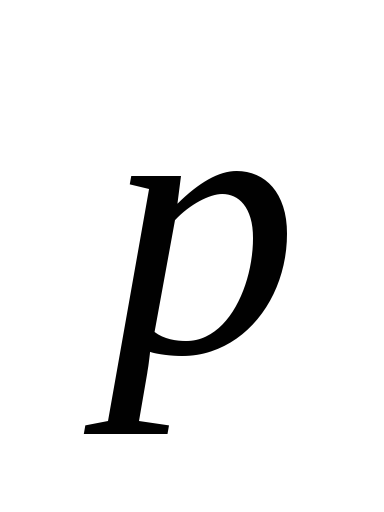 =16.
=16.
Найти вектор
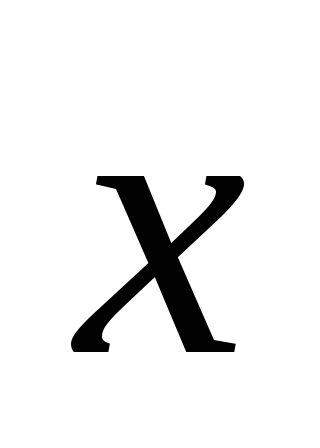 ,
зная, что
,
зная, что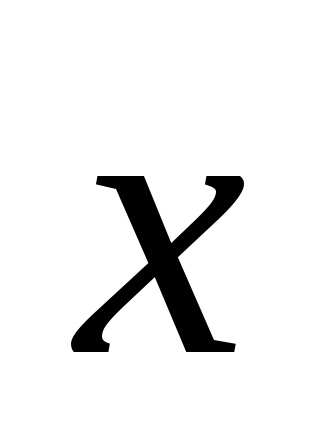 Оz,
Оz,
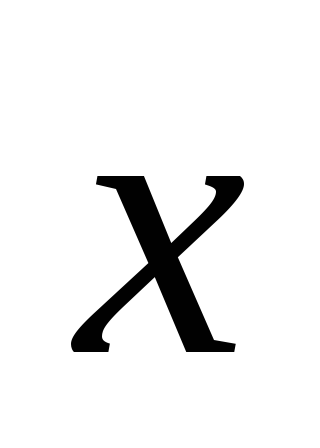
 ,
,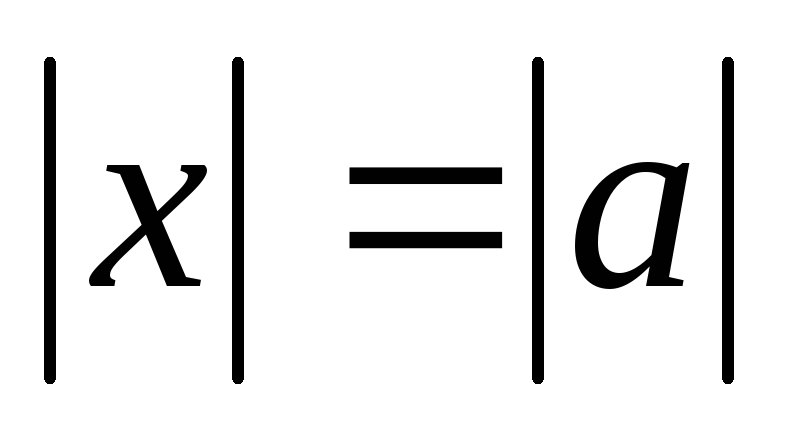 ,
где
,
где =–3;
5; 4.
=–3;
5; 4.Даны векторы
 =0;
2; 1,
=0;
2; 1,
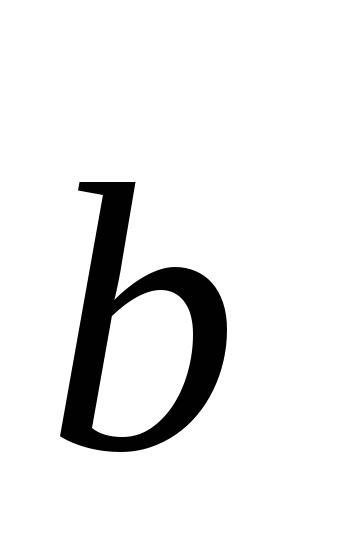 =1;
0; 2,
=1;
0; 2,
 =1;
1; 1.
Найти вектор
=1;
1; 1.
Найти вектор
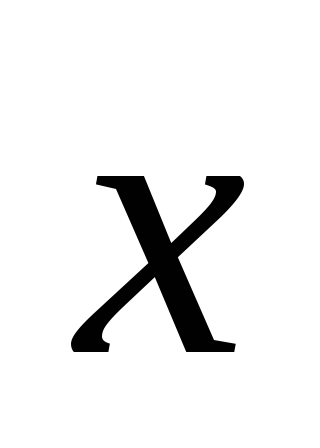 ,
если
,
если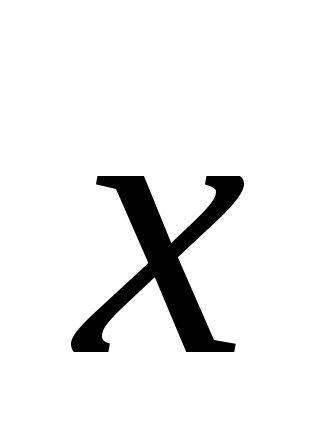
 ,
,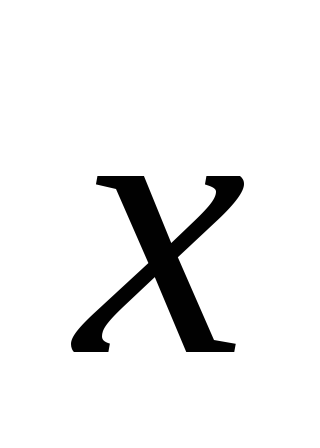
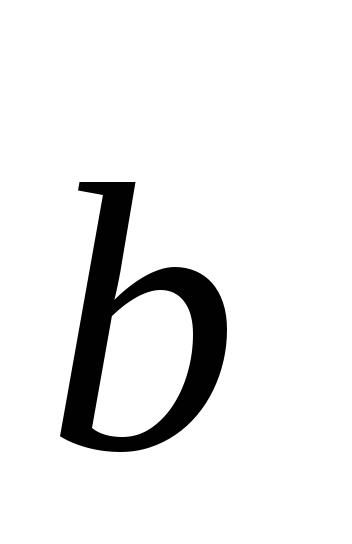 ,
,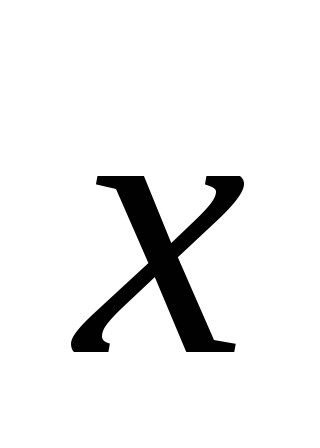
 =3.
=3.Найти вектор
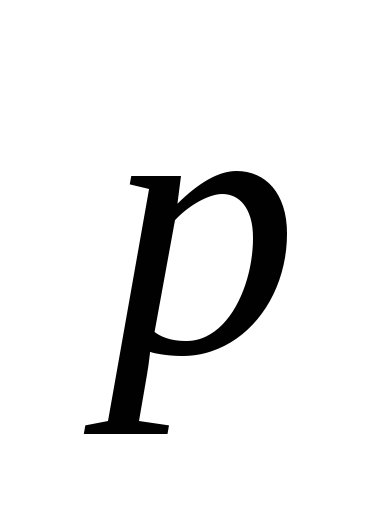 ,
зная, что он перпендикулярен к векторам
,
зная, что он перпендикулярен к векторам =2;
–1; 0
и
=2;
–1; 0
и
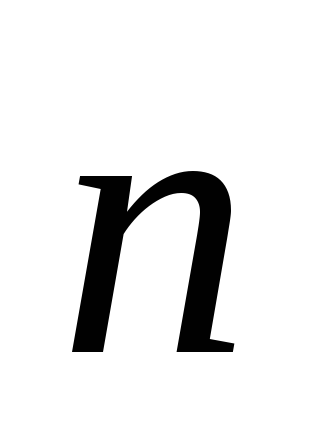 =2;
–2; 1,
образует с осью Оy
тупой угол и
=2;
–2; 1,
образует с осью Оy
тупой угол и  =5.
=5.
30.
Найти вектор
![]() ,
зная, что
,
зная, что![]()
![]() ,
,![]()
![]() ,
,![]() 1;
1; 1=–18,
где
1;
1; 1=–18,
где
![]() =2;
–3; 1,
=2;
–3; 1,
![]() =–2;
1;1.
=–2;
1;1.
Задание 9.
Даны вершины четырехугольника А(1; –2; 2), В(1; 4; 0), С(–4; 1; 1), Д(–5;–5;3). Доказать, что его диагонали АС и ВД взаимно перпендикулярны.
Проверить, что векторы
 ={7;
6; –6} и
={7;
6; –6} и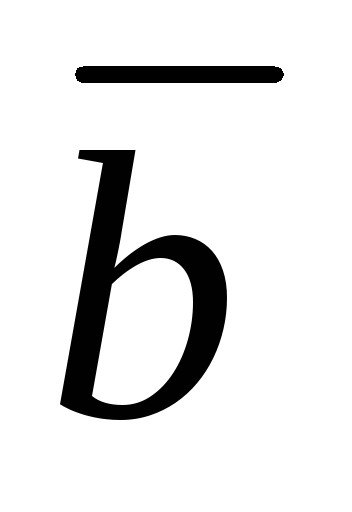 ={6;
2; 9} могут быть взяты за ребра куба. Найти
третье ребро.
={6;
2; 9} могут быть взяты за ребра куба. Найти
третье ребро.Дан треугольник АВС с вершинами в точках А(3; 5; 4), В(5; 8; 3), С(1; 9; 9). Найти длину высоты, опущенной из вершины С.
Точки А(1; 2) и С(3; 6) – противоположные вершины квадрата. Найти координаты двух других его вершин.
Зная векторы
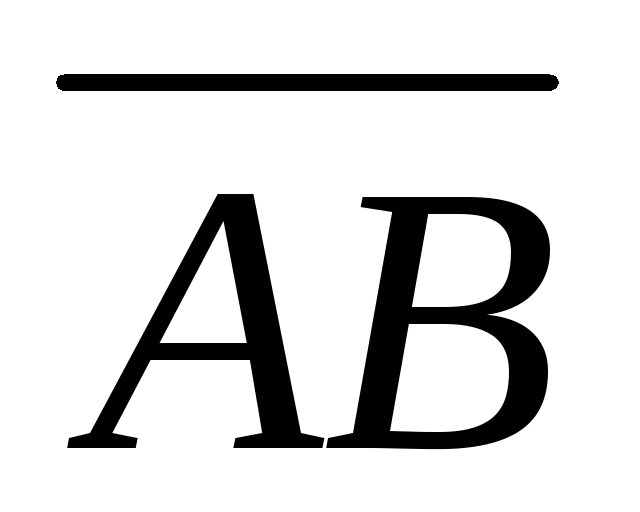 ={1;
2; –1} и
={1;
2; –1} и =
{2; 0; –4}, совпадающие с двумя сторонами
треугольника, найти угол при вершинеА
и площадь треугольника.
=
{2; 0; –4}, совпадающие с двумя сторонами
треугольника, найти угол при вершинеА
и площадь треугольника.Доказать, что векторы
 и
и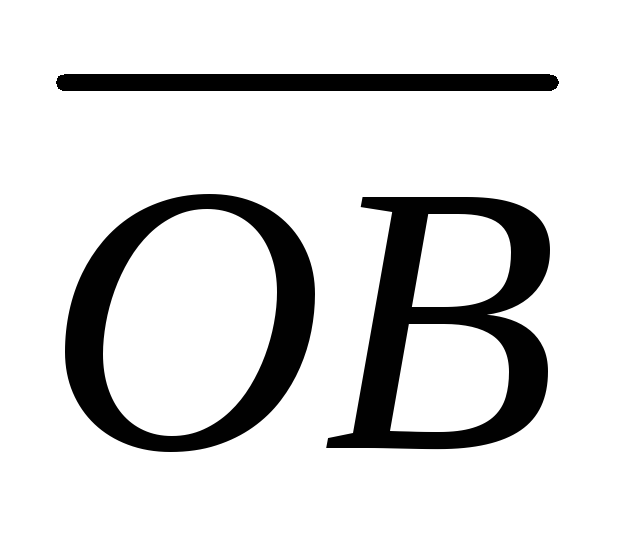 ,
гдеА(3;
6; –2), В(6;
–2; 3) могут быть взяты за ребра кеба.
Найти конец С
третьего ребра.
,
гдеА(3;
6; –2), В(6;
–2; 3) могут быть взяты за ребра кеба.
Найти конец С
третьего ребра.Даны вершины четырехугольника А(1; 2; 3), В(7; 3; 2), С(–3; 0; 6) и Д(9; 2; 4). Доказать, что его диагонали взаимно перпендикулярны.
Даны вершины треугольника А(4; 1; 0), В(2; 2; 1) и С(6; 3; 1). Найти длину высоты опущенной из вершины В.
Проверить, что векторы
 ={12;
–3; –3} и
={12;
–3; –3} и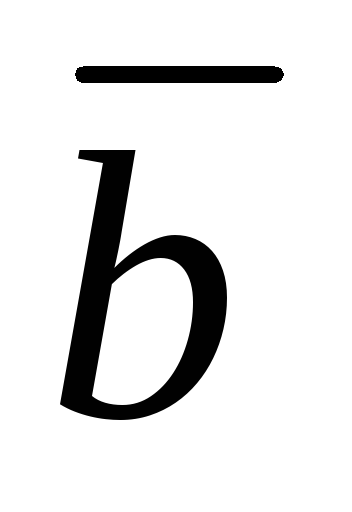 ={4;
5; 11} могут быть взяты за ребра куба.
Найти третье ребро.
={4;
5; 11} могут быть взяты за ребра куба.
Найти третье ребро.Зная векторы
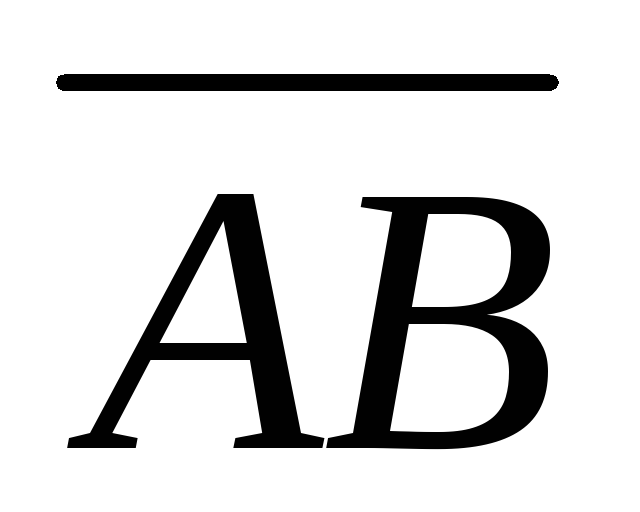 ={2;
–2; –3} и
={2;
–2; –3} и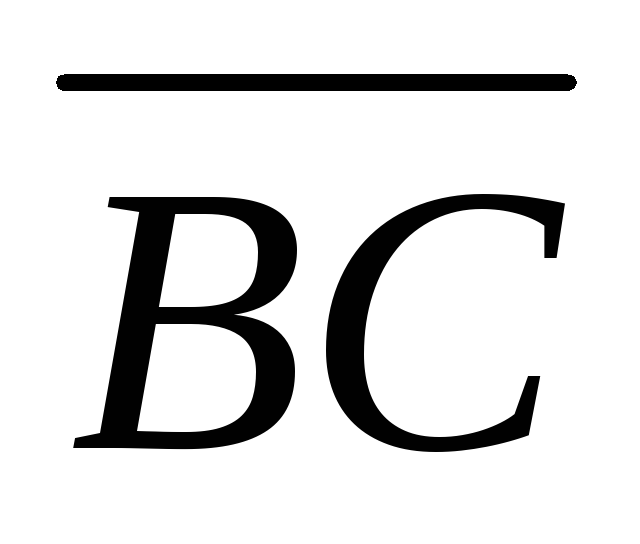 ={2;
2; 9}, совпадающие с двумя сторонами
треугольника, найти угол при вершинеС
и площадь треугольника.
={2;
2; 9}, совпадающие с двумя сторонами
треугольника, найти угол при вершинеС
и площадь треугольника.Даны три последовательные вершины параллелограмма: А(–3; –2; 0), В(3; –3; 1) и С(5; 0; 2). Найти его четвертую вершину и угол между диагоналями АС и ВД.
Проверить, что точки А(3; –1; 2), В(1; 2; –1), С(–1; 1; –3), Д(3; –5; 3) служат вершинами трапеции. Найти длины ее параллельных сторон.
Зная векторы
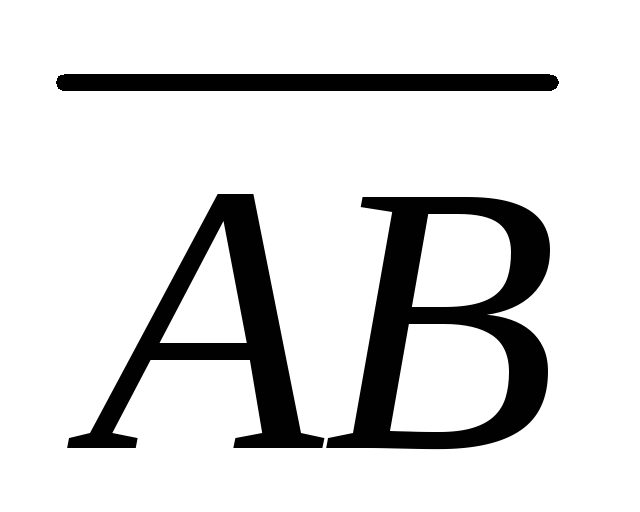 ={2;
–2; 1} и
={2;
–2; 1} и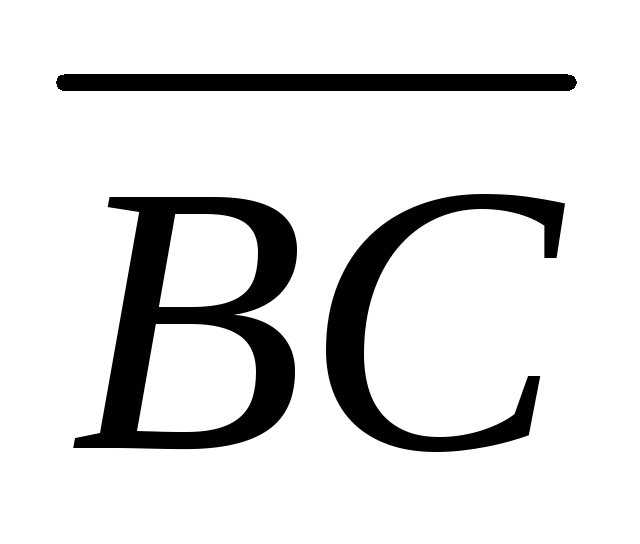 ={–4;
1; –3}, совпадающие с двумя сторонами
треугольника, найти угол при вершинеА
и высоту ВD.
={–4;
1; –3}, совпадающие с двумя сторонами
треугольника, найти угол при вершинеА
и высоту ВD.Доказать, что четырехугольник с вершинами А(2; 1; –4), В(1; 3; 5), С(7; 2; 3), D(8; 0; –6) есть параллелограмм. Найти длины его сторон.
Даны три последовательные вершины параллелограмма: А(1; 1; 4), В(2; 3; –1), С(–2; –2; 0). Найти его четвертую вершину и угол между диагоналями.
Проверить, что векторы
 =
=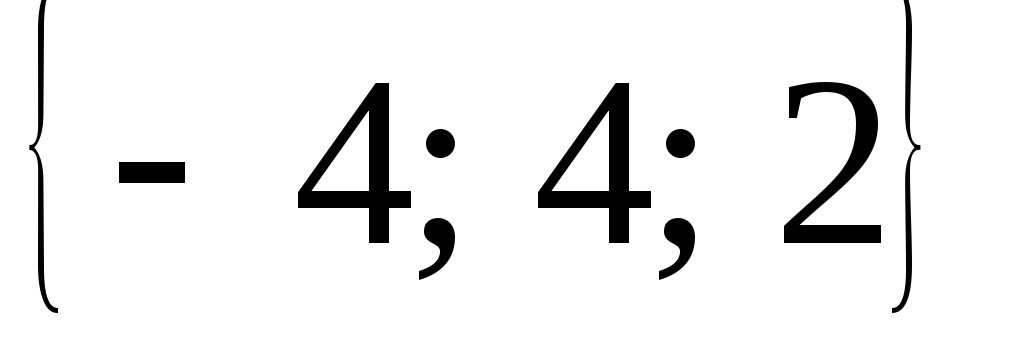 ,
,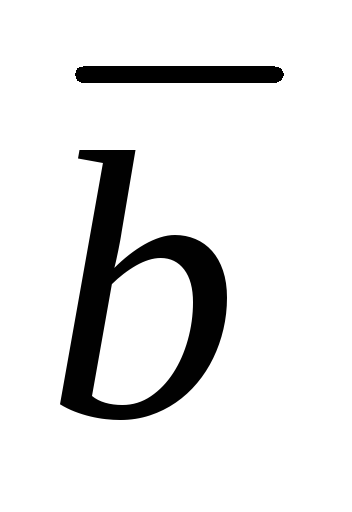 =
=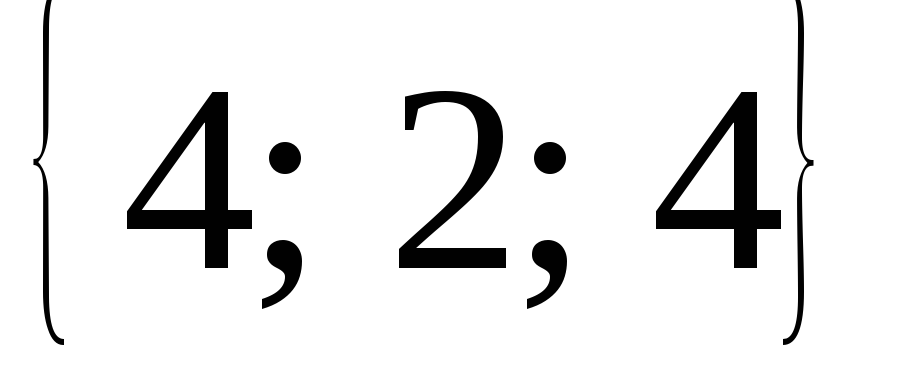 могут быть взяты за ребра куба. Найти
третье ребро .
могут быть взяты за ребра куба. Найти
третье ребро .Зная векторы
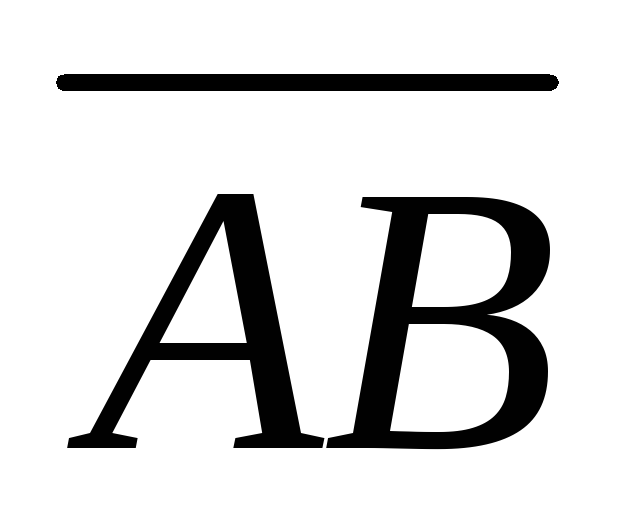 =
=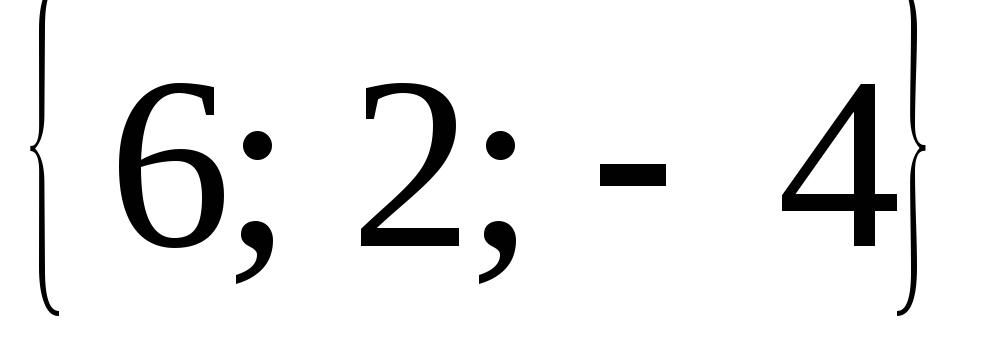 ,
,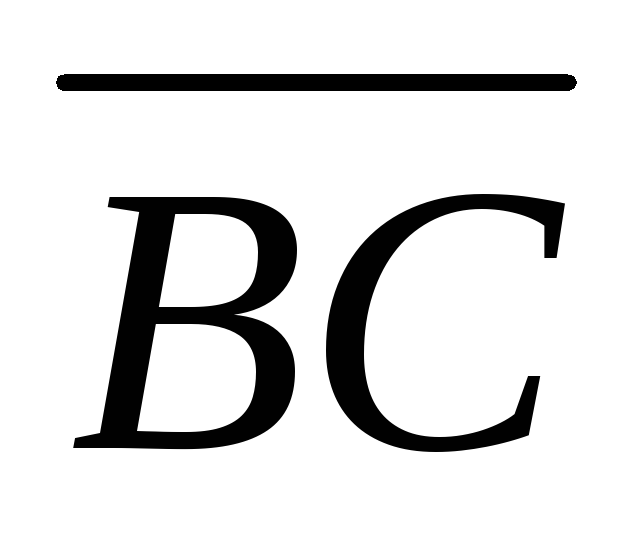 =
=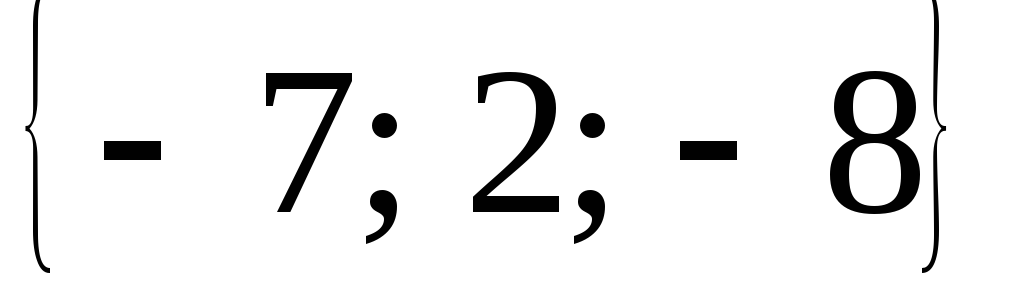 ,
совпадающие со сторонами треугольника,
найти угол при вершинеА
площадь треугольника.
,
совпадающие со сторонами треугольника,
найти угол при вершинеА
площадь треугольника.Дан треугольник АВС с вершинам в точках А(–1;–2;4), B(–4;–2;0) и С(3;–2;1). Найти длину высоты, опущенной из вершины С.
Даны вершины четырехугольника А(1;–2; 2), В(1; 4; 0), С(–4; 1; 1), D(–5;–5; 3). Доказать, что его диагонали АС и ВD взаимно перпендикулярны.
Даны 3 последовательные вершины параллелограмма А(1;–2;3), В(3; 2; 1), С(6; 4; 4). Найти его четвертую вершину и угол между диагоналями.
Зная векторы
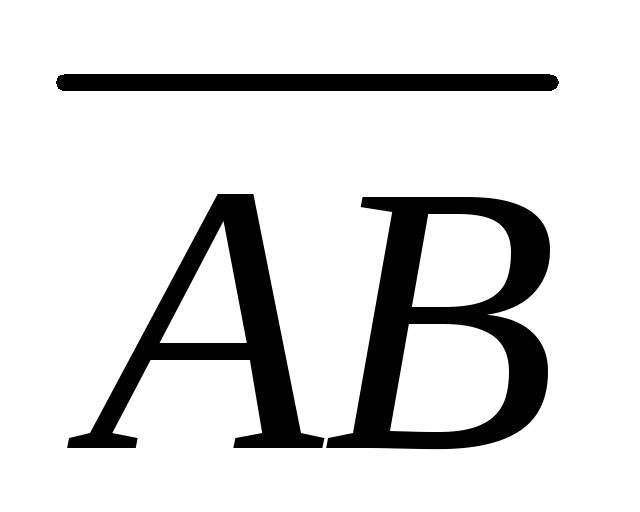 =
=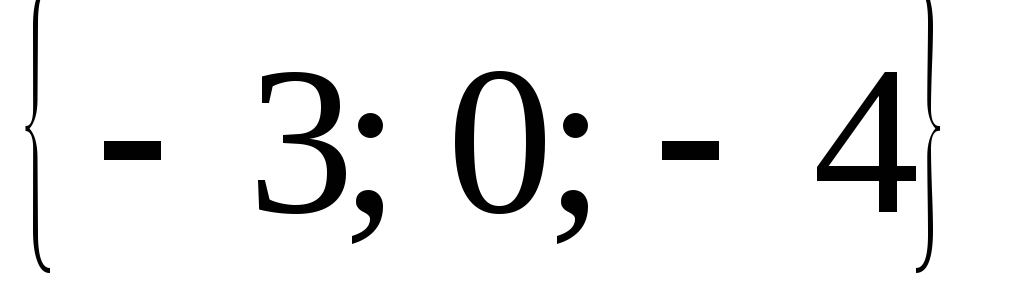 ,
, =
= ,
совпадающие с двумя сторонами
треугольника, найти угол при вершинеА
и высоту ВD.
,
совпадающие с двумя сторонами
треугольника, найти угол при вершинеА
и высоту ВD.Доказать, что векторы
 =
=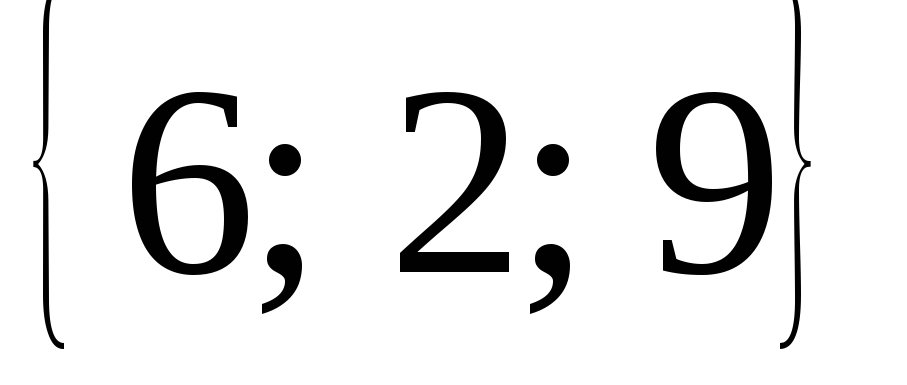 ,
,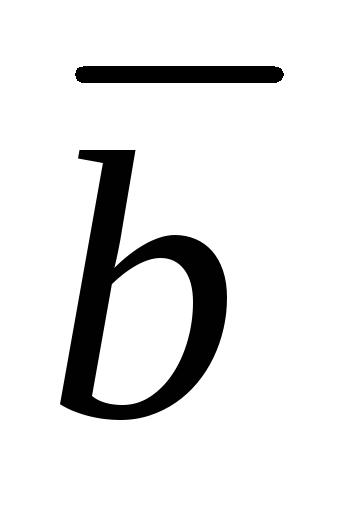 =
=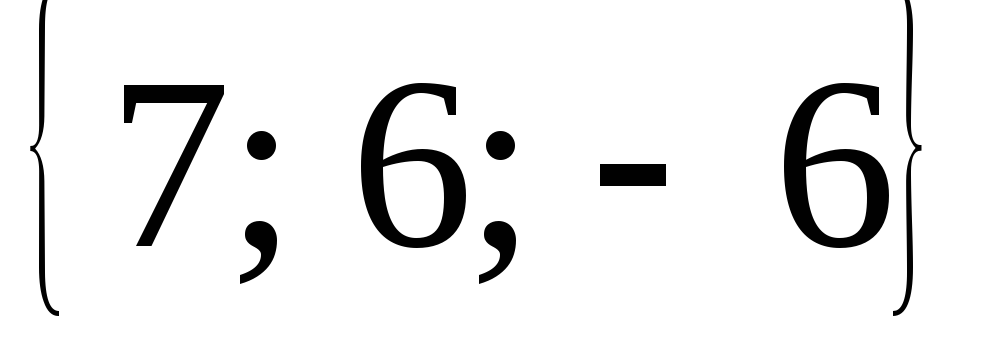 могут быть взяты за ребра куба. Найти
третье ребро.
могут быть взяты за ребра куба. Найти
третье ребро.Дан треугольник АВС с вершинами в точках А(3; 2; –3), В(5; 1; –1), С(1; –2; 1). Найти внутренние углы этого треугольника.
Даны вершины четырехугольника А(7; 3; 2), В(–3; 0; 6), С(9; 2; 4), D(1; 2; 3). Доказать, что его диагонали взаимно перпендикулярны.
Проверить, что точки А(3; –1; 2), В(1; 2; –1), С(–1; 1; –3), D(3; –5; 3) служат вершинами трапеции. Найти длины ее параллельных сторон.
Векторы
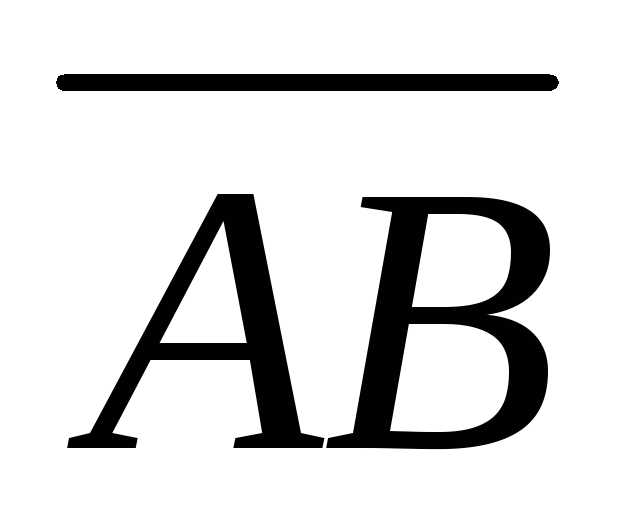 =
=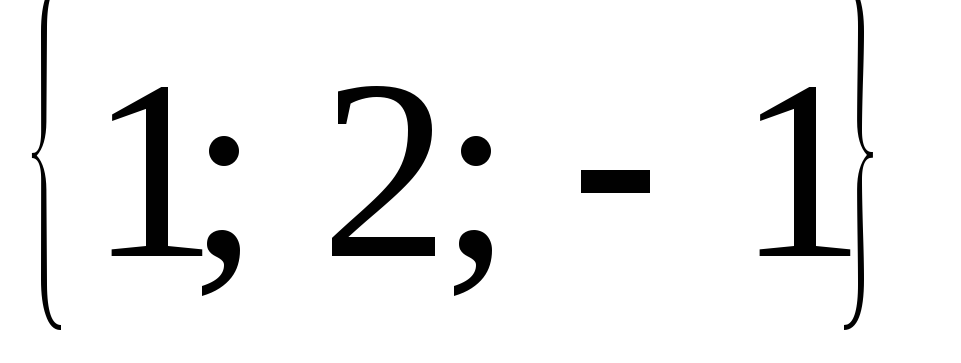 и
и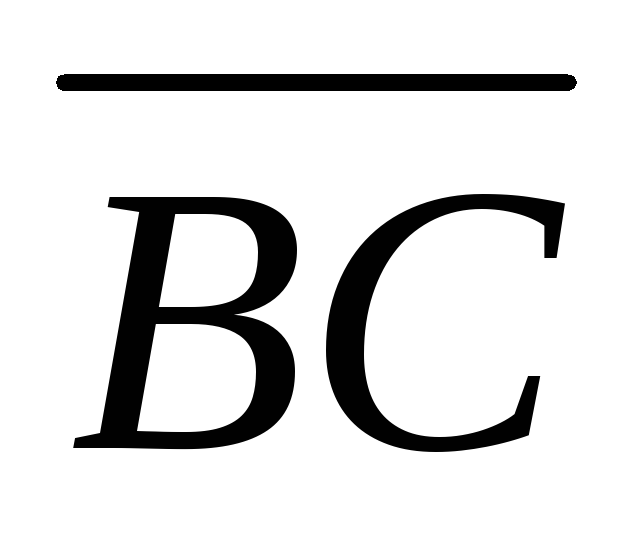 =
=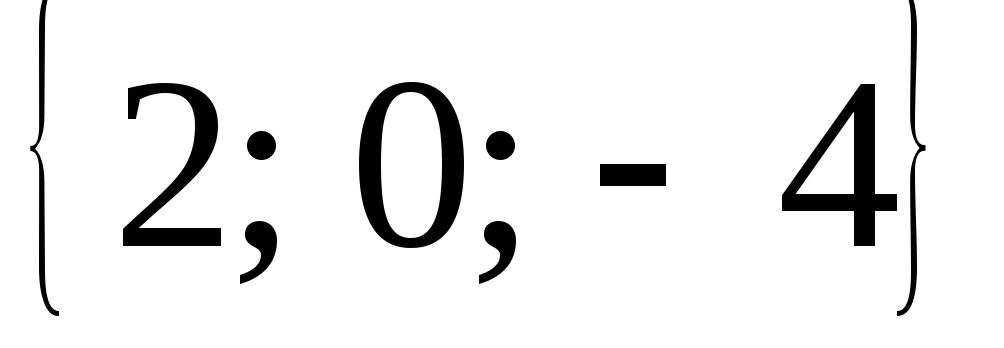 совпадают с двумя сторонами треугольника
.Найти высоту, опущенную из вершиныС.
совпадают с двумя сторонами треугольника
.Найти высоту, опущенную из вершиныС.Доказать, что векторы
 =
=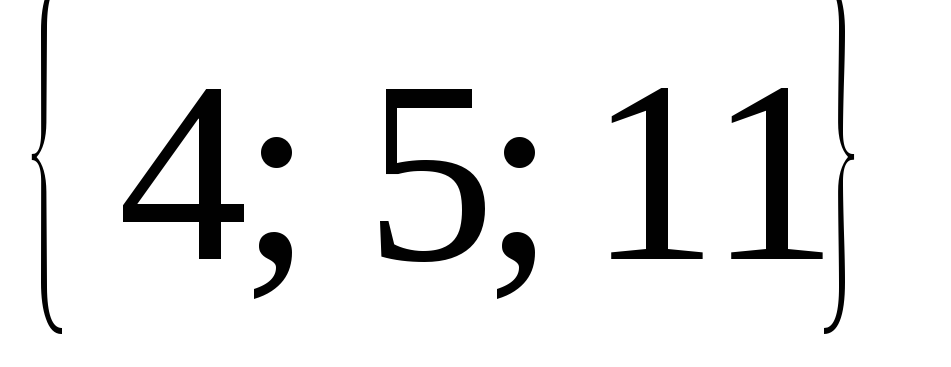 и
и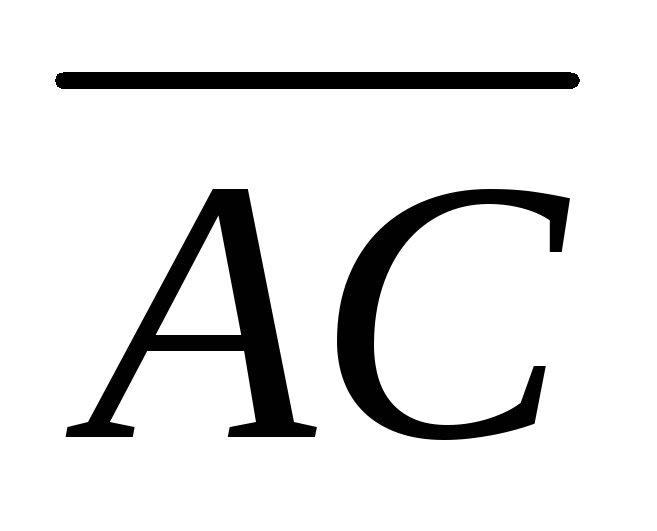 =
= могут быть взяты за ребра куба. Найти
третье ребро.
могут быть взяты за ребра куба. Найти
третье ребро.Даны вершины треугольника А(4; 1; 0), В(2; 2; 1) и С(6; 3; 1). Найти длину высоты, опущенной из вершины А.
Даны три последовательные вершины параллелограмма А(–3; –2; 0), В(3; –3; 1), С(5; 0; 2). Найти его четвертую вершину и угол между диагоналями.
Зная векторы
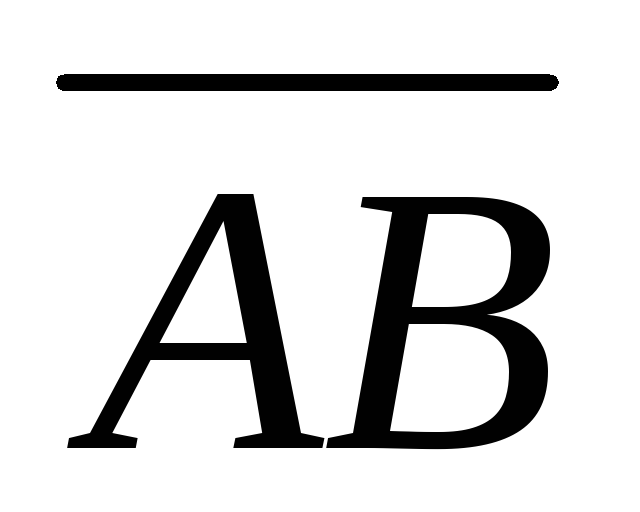 =
=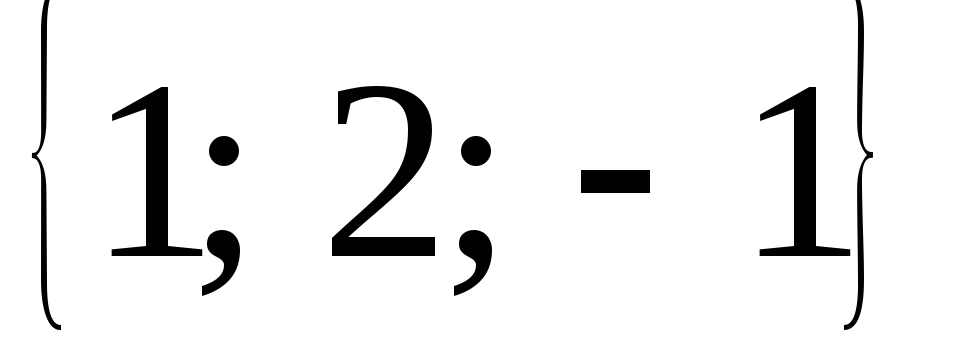 и
и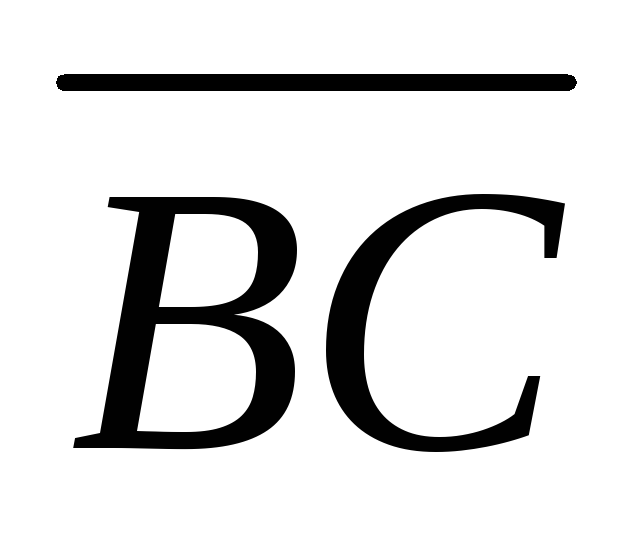 =
=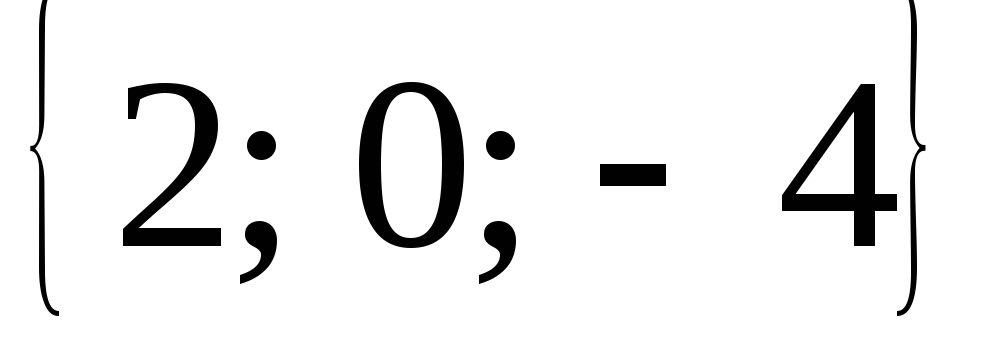 ,
совпадающие с двумя сторонами
треугольника, найти угол при вершинеС
и площадь треугольника.
,
совпадающие с двумя сторонами
треугольника, найти угол при вершинеС
и площадь треугольника.
