Решение

Исходная матрица имеет вид:

7	13	5	8	6
11	5	8	4	5
8	5	8	9	4
6	4	10	1	5
3	2	7	6	2

Проводим редукцию матрицы по строкам. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.

2	8		3	1	5
7	1	4		1	4
4	1	4	5		4
5	3	9		4	1
1		5	4		2

Затем такую же операцию редукции проводим по столбцам, для чего в каждом столбце находим минимальный элемент.

1	8		3	1
6	1	4		1
3	1	4	5
4	3	9		4
		5	4
1	0	0	0	0

После вычитания минимальных элементов получаем полностью редуцированную матрицу.

Методом проб и ошибок проводим поиск допустимого решения, для которого все назначения имеют нулевую стоимость.

Фиксируем нулевое значение в клетке (1, 3). Другие нули в строке 1 и столбце 3 вычеркиваем. Для данной клетки вычеркиваем нули в клетках (5; 5)

Фиксируем нулевое значение в клетке (2, 4). Другие нули в строке 2 и столбце 4 вычеркиваем. Для данной клетки вычеркиваем нули в клетках (5; 5)

Фиксируем нулевое значение в клетке (3, 5). Другие нули в строке 3 и столбце 5 вычеркиваем. Для данной клетки вычеркиваем нули в клетках (5; 5)

В итоге получаем следующую матрицу:

1	8	[0]	3	1
6	1	4	[0]	1
3	1	4	5	[0]
4	3	9	[-0-]	4
		5	4	[-0-]

Поскольку расположение нулевых элементов в матрице не позволяет образовать систему из 5-х независимых нулей (в матрице их только 3), то решение недопустимое.

Проводим модификацию матрицы. Вычеркиваем строки и столбцы с возможно большим количеством нулевых элементов: строку 5, столбец 4, строку 1, столбец 5

Получаем сокращенную матрицу (элементы выделены):

1	8		3	1
6	1	4		1
3	1	4	5
4	3	9		4
		5	4

Минимальный элемент сокращенной матрицы (min(6, 1, 4, 3, 1, 4, 4, 3, 9) = 1) вычитаем из всех ее элементов:

1	8		3	1
5	0	3		1
2	0	3	5
3	2	8		4
		5	4

Затем складываем минимальный элемент с элементами, расположенными на пересечениях вычеркнутых строк и столбцов:

1	8		4	2
5		3		1
2		3	5
3	2	8		4
		5	5	1

Проводим редукцию матрицы по строкам. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль. Затем такую же операцию редукции проводим по столбцам, для чего в каждом столбце находим минимальный элемент. После вычитания минимальных элементов получаем полностью редуцированную матрицу.

Методом проб и ошибок проводим поиск допустимого решения, для которого все назначения имеют нулевую стоимость.

Фиксируем нулевое значение в клетке (1, 3). Другие нули в строке 1 и столбце 3 вычеркиваем.

Фиксируем нулевое значение в клетке (2, 2). Другие нули в строке 2 и столбце 2 вычеркиваем.

Фиксируем нулевое значение в клетке (3, 5). Другие нули в строке 3 и столбце 5 вычеркиваем.

Фиксируем нулевое значение в клетке (4, 4). Другие нули в строке 4 и столбце 4 вычеркиваем.

Фиксируем нулевое значение в клетке (5, 1). Другие нули в строке 5 и столбце 1 вычеркиваем.

В итоге получаем следующую матрицу:

1	8	[0]	4	2
5	[0]	3	[-0-]	1
2	[-0-]	3	5	[0]
3	2	8	[0]	4
[0]	[-0-]	5	5	1

Количество найденных нулей равно k = 5. В результате получаем эквивалентную матрицу :

1	8		4	2
5		3		1
2		3	5
3	2	8		4
		5	5	1

Методом проб и ошибок определяем матрицу назначения Х:

1	8	[0]	4	2
5	[0]	3	[-0-]	1
2	[-0-]	3	5	[0]
3	2	8	[0]	4
[0]	[-0-]	5	5	1

Следовательно, минимальные суммарные затраты по времени, равны: .

Ответ: .

5. Найти и построить на координатной плоскости область определения функции двух действительных переменных:

Решение

Составим систему требований, которые определяют ОДЗ:

.

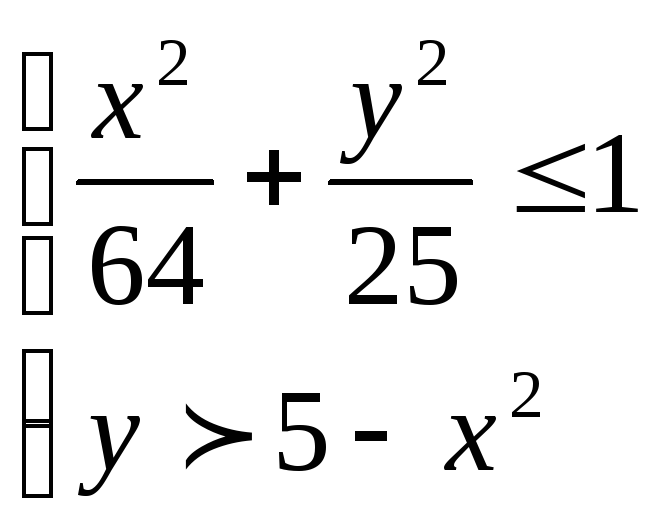- область внутренней части эллипса, который имеет полуоси и . - область выше линии параболы.

Построим полученную область определения:

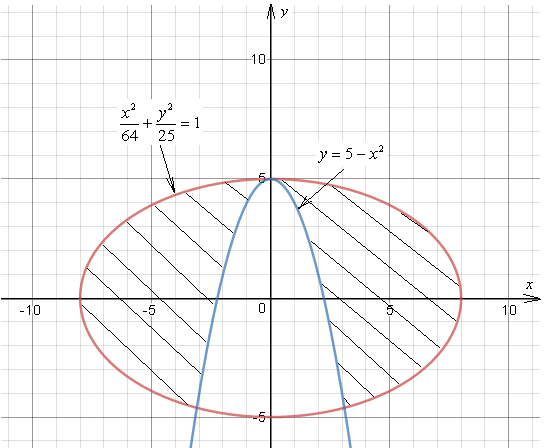
Ответ: смотреть выше.

6. Исследовать на экстремум функцию двух действительных переменных:

Решение

1) Находим область определения функции , кроме .

2) Находим первые частные производные и :

3) Составим систему уравнений . В области действительных чисел получим решение: .

4) Находим вторые частные производные:

, составляем выражение:

.

5) Делаем вывод о наличии экстремумов.

Так как и , то функция в точке имеет минимум, который равен .

Ответ: функция в точке имеет минимум, .

7. Исследовать на условный экстремум функцию двух действительных переменных при условии .

Решение

Геометрическая интерпретация данной задачи такова: требуется найти наибольшее и наименьшее значение аппликаты плоскости для точек ее пересечения с цилиндром .

Выразить одну переменную через другую из уравнения связи и подставить ее в функцию несколько затруднительно, поэтому будем использовать метод Лагранжа.

Обозначив , составим функцию Лагранжа:

,

Запишем систему уравнений для определения стационарных точек функции Лагранжа:

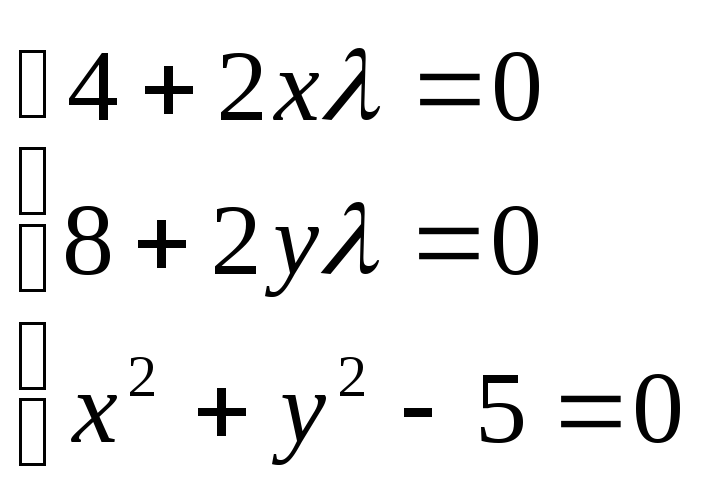
Если предположить , то первое уравнение станет таким: 4=0. Полученное противоречие говорит о том, что . При условии из первого и второго уравнений имеем: , . Подставляя полученные значения в третье уравнение, получим:

.

Тогда получим:

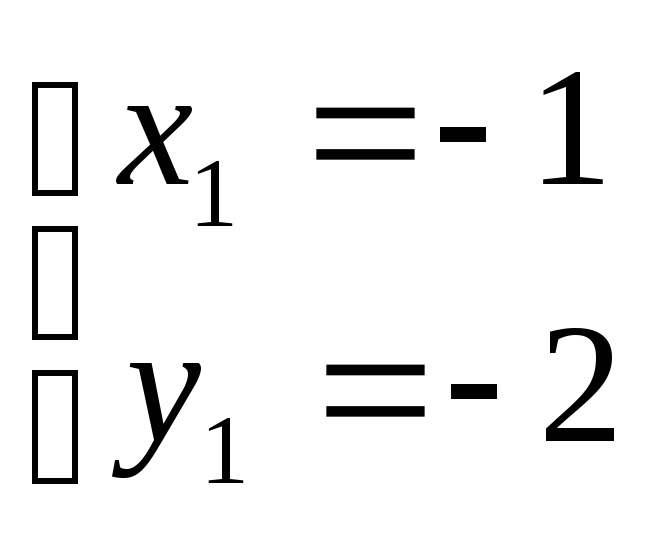: и : .

Исследуем знаки дифференциала второго порядка . Если окажется, что в стационарной точке , то функция достигает там максимума, если же  – то минимума.

Найдём частные производные второго порядка:

, , и составим этот дифференциал: .

: , значит, функция достигает минимума в точке  , который равен .

: , значит, функция достигает максимума в точке  , который равен .

Ответ: ; .

8. Автомобильный концерн «Кайзер», выпускающий автомобили марки «Родео» трёх основных модификаций: СЕДАН, ХЭТЧБЭК и УНИВЕРСАЛ, провёл маркетинговые исследования и проанализировал объёмы продаж машин за три сезона: ОСЕНЬ, ЗИМА, ВЕСНА. В зависимости от времени года эксперты определили нормы прибыли (в условных единицах), которые могут быть записаны в виде матрицы выигрышей концерна «Кайзер» конкурирующие стратегии (сезонный спрос на автомобили): – спрос на автомобили ОСЕНЬЮ; – спрос на автомобили ЗИМОЙ; – спрос на автомобили ВЕСНОЙ.

Определить оптимальные смешанные стратегии для концерна «Кайзер» по выпуску автомобилей «Родео», обеспечивающий наибольшую прибыль в любое время года.

	Стратегии
- выпуск автомобилей «Родео» типа СЕДАН		1	2	6
- выпуск автомобилей «Родео» типа ХЭТЧБЭК		2	5	3
- выпуск автомобилей «Родео» типа УНИВЕРСАЛ		4	3	2