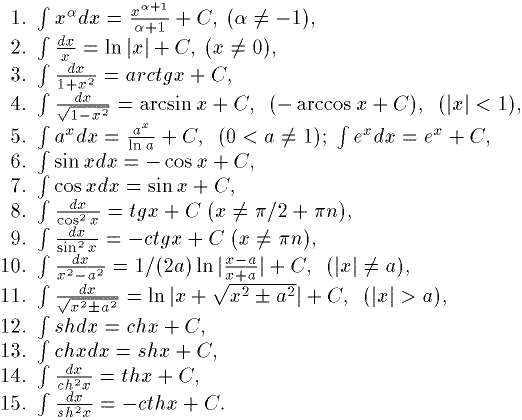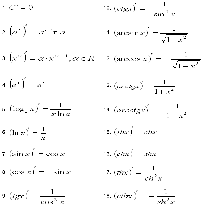Формулы

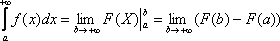
 и  

; ; 

  и .

Проведем универсальную тригонометрическую подстановку: , 

1. Ряды. Пусть a1,a2,a3…a_n – числовая последовательность. Определение: Выражение вида a₁+a₂+…+a_n или 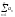a1,a2,a3…a_{n –} члены ряда an – n-й член ряба (общий член ряда) Сумма n первых членов ряда называется n-ной частичной суммой и обозначается Sn, Sn=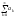 Определение: Числовой ряд сходится, если сходится последовательность его частичных сумм, т.е. сущ-ет конечный предел при x∞ Sn=S. Тогда S- сумма ряды Если посл-ть Sn не имеет конечного предела, то числовой ряд расходится.

2. Необходимое условие сходимости. Теорема: Если ряд сходится, то lim его общего члена равен 0. Док-во: Пусть S=limSn Sn=Sn-1+an, поэтому liman=lim(Sn-Sn-1) или =limSn-limSn-1=S-S=0 Следствие: ( достаточное условие расходимости): Если liman≠0 то 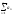- расходится Док-во: (от противного): Пусть 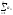- сходится, тогда по теореме liman=0 – противоречие.

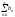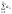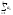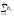3. Признак сравнения. Теорема: (признак сравнения) Если сущ-ет номер n0,такой, что для любого n>=n0 0<=an<=bn(1), то 1. из сходимости =>сходимость 2. из расходимости => расходимость Док-во: Пусть n0=1, тогда 1. Sn=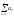 - n-ная частичная сумма ряда an. /S\n= - n-ная частичная сумма ряда bn. Из (1) => Sn<=/S\n для любого n т.к. bn- сходится, то {/S\n} – сходится => посл-ть ограниченна => ограниченна {Sn} и значит что пос-ть сходится, значит - сходится. 2. Пусть - расходится => {Sn} – неограниченна => {/S\n}- неогр. => 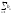- расх. Пусть n0>1 тогда д.р. 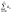и 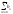- т.к. отбрасывание конечного числа элементов ряда не влияет на сходимость . Предельный признак сравнения: Теорема: Если an>0, bn>0, для любого n>n0 и сущ-ет конечный предел an/bn ≠0, то ряды 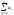и 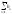- сходятся или расходятся одновременно. Док-во: Пусть liman/bn=L для любого ε>0 сущ-ет n_ε т.ч. для любого n>n_ε |an/bn-L|<ε; L-ε<an/bn<L+ε. Bn>0 => (L-ε)bn<an<(L+ε)bn если 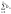- сходится, то (L+ε) – сходится, и из === по признаку сравнения следует, что 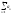- сходится, если - расходится, то (L-ε) 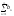- расх, то из -------- следует - расходится.

4. Признак Даламбера. Теорема: Пусть an>0 для любого n, если lim(a_n+1/a_n)=L, то 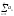- сходится, если L<1, расходится если L>1. 0<(a­_n+1/a_n)<1, lim(a_n+1/a_n)=L<1; L<θ<1 т.к. сходимость или расходимость ряда не нарушается в результате изменения или удаления конечного числа его членов будем считать: 0<(a­_n+1/a_n)<1 для любого n; тогда 0<a₂/a₁<θ; a₂<θ; 0< a₂/a₁<θ …… θ – сходится (геометрическая прогрессия с q=0) => по теореме сравнения сходится ряд 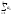. Lim(a_n+1/a_n)=L>1, a_n+1/a_n>1 почти для всех n => начиная с некоторого номера члены ряда возрастают т.е. не выполняется условие liman=0 т.е. ряд расх.

5. Радикальный признак Коши. Пусть an>=0 для любого n и сущ. Предел 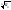=L. Тогда, если L>1, то ряд сходится… Если L<1, то ряд расходится.