1,057, Или 105,7%.

б) базисные 1,162, или 116,2%.

1,194, Или 119,4%.

Как видно из вычислений, цепные общие индексы цен имеют переменные веса на уровне отчетного периода. Для таких индексов нет взаимосвязи между цепными и базисными индексами, что характерно для всех качественных индексов.

Исчислим общие индексы физического объема товарооборота:

а) цепные 1,104, или 110,4%,

0,795, Или 79,5%.

б) базисные 0,877, или 87,7%.

1,104, Или 110,4%.

Данные примера показывают, что цепные и базисные индексы количественных показателей взвешиваются по постоянным весам, следовательно, между ними имеется связь: произведение цепных индексов равно базисному:

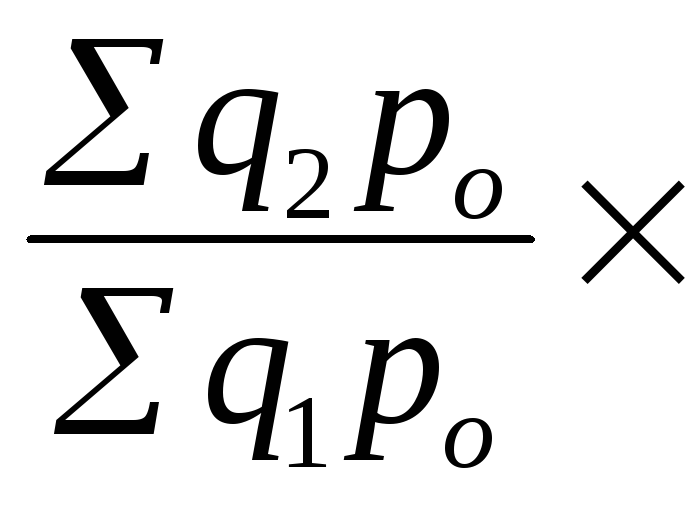
или 1,104 × 0,795 = 0,877.

От базисных индексов можно перейти к цепным, как это показано выше.

№ 5. Имеются данные о выпуске продукции «А» по двум заводам:

№ завода	Базисный период			Отчетный период
	Произ-ведено продук-ции, тыс. шт.	Себестоимость единицы, руб.	Удельный вес продук-ции, %	Произ-ведено продук-ции, тыс. шт.	Себестоимость единицы, руб.	Удельный вес продукции, %
	qo	zo	do	q1	z1	d1
1	60	24	50	80	20	40
2	60	20	50	120	18	60
	120		100	200		100

Вычислить: 1) индекс себестоимости переменного состава; 2) индекс себестоимости постоянного состава; 3) индекс структурных сдвигов.

Решение. 1. Вычислим индекс себестоимости переменного состава, который равен соотношению средней себестоимости продукции по двум заводам:

Средняя себестоимость продукции по двум заводам в отчетном и базисном периодах равна:

18,8 Руб.

22 Руб.

Следовательно, индекс себестоимости переменного состава равен:

или 85,5%.

Индекс показывает, что средняя себестоимость изделия по двум заводам снизилась на 14,5%. Это снижение обусловлено изменением себестоимости продукции по каждому заводу и изменением структуры продукции (удельного веса продукции заводов). Выявим влияние каждого из этих факторов на динамику средней себестоимости, исчислив индексы себестоимости постоянного состава и структурных сдвигов.

2. Индекс себестоимости постоянного состава (индекс в постоянной структуре):

0,870.

Себестоимость продукции по двум заводам в среднем снизилась на 13%.

3. Индекс структурных сдвигов равен:

.

=

= 21,6 : 22,0 = 0,982, или 98,2%.

Средняя себестоимость изделия в отчетном периоде снизилась дополнительно на 1,8% за счет изменения структуры, т.е. за счет увеличения доли продукции 2-го завода с 50 до 60%, на котором уровень себестоимости продукции был ниже по сравнению с первым заводом.

Исчисленные выше индексы можно вычислять по удельным весам продукции заводов, выраженных в коэффициентах:

а) индекс себестоимости переменного состава –

0,855;

б) индекс себестоимости постоянного состава-

0,870;

в) индекс структурных сдвигов –

0,982

Индекс структурных сдвигов может быть вычислен так же с помощью взаимосвязи индексов. Известно, что индекс переменного состава равен произведению индексов постоянного состава и структурных сдвигов:

Следовательно, 0,982.