Для первого года
I
квартал
;
II
квартал
;
III
квартал
и т.д. (см. табл. 7, гр. 5).
Далее необходимо
найти для каждого квартала процентные
отношения эмпирических уровней ряда
к теоретическим уровням
,
т.е.
100%.
Тогда, для первого года
I
квартал
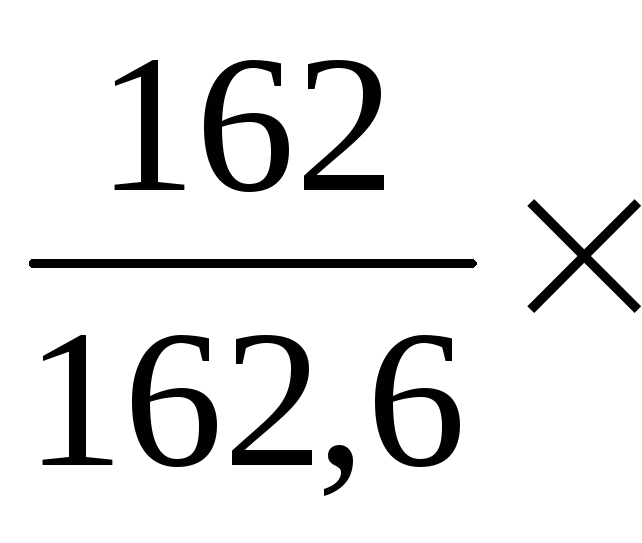100
= 99,6%.
II
квартал
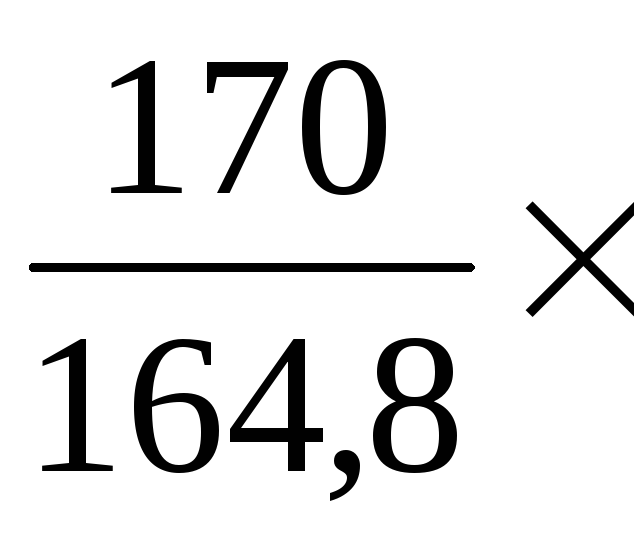100
= 103,2% и т.д.
для третьего года
IV
квартал
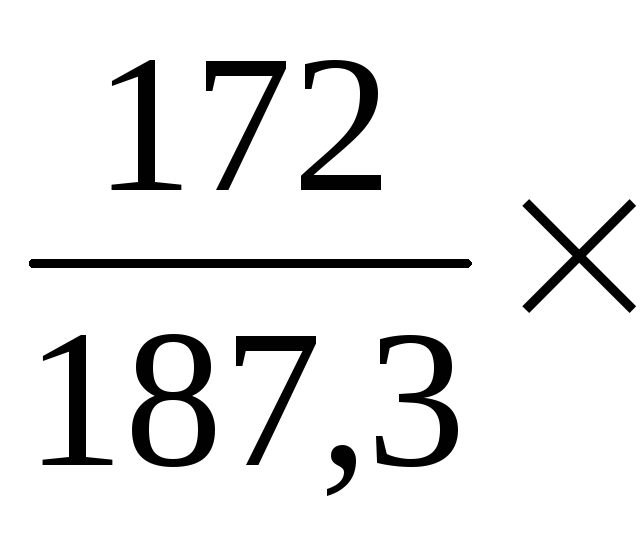100
= 91,8%.
После этого нужно
просуммировать полученные процентные
отношения
за три года по одноименным кварталам
(см. с. 28 табл. 8):
I квартал 99,6+92,7+87,4=279,7;
II квартал 103,2+111,0+123,0=337,2 и т.д.
Затем следует исчислить индексы сезонности (см. табл. 8, гр.11)
Т а б л и ц а 8
Динамика заготовок сельскохозяйственной продукции области
|
Квар-талы |
Фактические
данные,
|
Выравненные
данные,
|
Фактические данные в процентах к выравненным,
|
Сумма процентных отношений (гр. 7+ +гр. 8+ +гр. 9) |
Индексы сезонности, %,
| ||||||
|
Первый год |
Второй год |
Третий год |
Первый год |
Второй год |
Третий год |
Первый год |
Второй год |
Третий год | |||
|
А |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
I |
162 |
159 |
158 |
162,6 |
171,6 |
180,8 |
99,6 |
92,7 |
87,4 |
279,7 |
93,2 |
|
II |
170 |
193 |
225 |
164,8 |
173,9 |
182,9 |
103,2 |
111,0 |
123,0 |
337,2 |
112,4 |
|
III |
177 |
178 |
187 |
167,1 |
176,1 |
185,2 |
105,9 |
101,1 |
101,0 |
308,0 |
102,7 |
|
IV |
151 |
168 |
172 |
169,4 |
178,4 |
187,3 |
89,1 |
94,2 |
91,8 |
275,1 |
91,7 |
|
Итого |
660 |
698 |
742 |
- |
- |
- |
- |
- |
- |
- |
100,0 |
,
Индексы сезонности характеризуют размеры заготовок сельскохозяйственной продукции в зависимости от времени года. Наибольший удельный вес заготовок сельскохозяйственной продукции приходится на второй квартал. Чтобы наглядно представить сезонную волну, индексы сезонности наносят на график.
Т е м а 6. ИНДЕКСЫ
ЗАДАЧИ
№ 1. Имеются следующие данные о продаже товаров в магазинах потребительской кооперации:
|
Товар |
Средняя цена единицы товара, руб. |
Количество проданного товара, тыс. ед. | ||
|
базисный период |
отчетный период |
базисный период |
отчетный период | |
|
Картофель, кг. |
0,4 |
0,5 |
90 |
100 |
|
Молоко, л |
0,5 |
0,4 |
20 |
30 |
В ы ч и с л и т ь: 1. Индивидуальные индексы цен и количества проданного товара. 2. Общие индексы: а) товарооборота; б) физического объема товарооборота; в) цен и сумму экономии или перерасхода от изменения цен.
П о к а ж и т е взаимосвязь между исчисленными индексами.
№ 2. Имеются следующие данные о количестве произведенной продукции и ее себестоимости по предприятию:
|
Продукция |
Количество произведенной продукции, тыс. шт. |
Себестоимость единицы продукции, руб. | ||
|
1986 г. |
1988 г. |
1986 г. |
1988 г. | |
|
КС |
3,0 |
3,2 |
1,0 |
1,0 |
|
МП |
4,0 |
5,0 |
2,0 |
1,8 |
|
КМ |
5,0 |
6,0 |
0,8 |
0,6 |
В ы ч и с л и т ь: 1. Индивидуальные индексы себестоимости и количества произведенной продукции; 2. общие индексы: а) затрат на продукцию; б) физического объема продукции; в) себестоимости и экономический эффект от снижения себестоимости продукции.
П о к а ж и т е взаимосвязь между исчисленными индексами.
№ 3. Имеются следующие данные о реализации товаров:
|
Товар |
Товарооборот в ценах соответствующего года, тыс.руб. |
Изменение цен в 1988 г. к 1985 г., % | |
|
1985 г. |
1988 г. | ||
|
Шерстяные ткани |
350 |
360 |
-10 |
|
Одежда |
800 |
861 |
+5 |
|
Обувь |
400 |
432 |
+8 |
В ы ч и с л и т ь: 1) общий индекс товарооборота; 2) общий индекс цен; 3) общий индекс физического объема товарооборота;
№ 4. Имеются следующие данные о продаже товаров в магазинах города:
|
Товарная группа |
Продано в 1986 г., тыс. руб. |
Изменение количества проданных товаров в 1988г. к 1986 г., % |
|
Трикотажные изделия |
650 |
+12 |
|
Швейные изделия |
500 |
+20 |
|
Ткани |
600 |
-5 |
В ы ч и с л и т ь: 1) общий индекс физического объема товарооборота в 1988 г. по сравнению с 1986 г. ; 2) общий индекс цен, если известно, что товарооборот в фактических ценах за этот период вырос на 12%;
№ 5. Имеются следующие данные о продаже товаров по району:
|
Товары |
Товарооборот в ценах соответствующего года, тыс.руб. |
Изменение цен в 1988 г. к 1985 г., % | |
|
1985 г. |
1988 г. | ||
|
Телевизоры |
550 |
600 |
-25 |
|
Радиоприемники |
315 |
360 |
-10 |
|
Часы |
220 |
255 |
-15 |
В ы ч и с л и т ь: 1) общий индекс товарооборота; 2) общий индекс цен; 3) общий индекс физического объема товарооборота; 4) прирост товарооборота за счет изменения количества проданных товаров и изменения цен.
№ 6. Имеются следующие данные о продаже сельскохозяйственных продуктов на колхозном рынке:
|
Товар |
Стоимость товара в фактических ценах, тыс.руб. |
Индексы количества проданных товаров в 1988 г. к 1987 г.в % | |
|
1987 г. |
1988 г. | ||
|
Картофель |
24 |
39 |
108 |
|
Молоко |
30 |
28 |
117 |
|
Мясо |
60 |
56 |
107 |
В ы ч и с л и т ь: 1. Общие индексы: а) стоимости товаров (товарооборота); б) физического объема товарооборота; в) цен; 2. изменение стоимости товара в 1988 г. по сравнению с 1987 г. за счет изменения количества проданного товара и изменения цен.
П о к а ж и т е взаимосвязь исчисленных индексов.
№ 7. Товарооборот республики в 1988 г. по сравнению с 1987 г. вырос на 6%, розничные цены в среднем повысились на 4%. Как изменился физический объем товарооборота?
№ 8. Как в среднем изменились цены, если известно, что товарооборот вырос на 18%, а физический объем товарооборота увеличился на 16%?
№ 9. В отчетном году по сравнению с базисным цены на сельскохозяйственные товары в среднем снизились на 3%, физический объем продажи товаров вырос в среднем на 15%. Как изменился товарооборот сельскохозяйственных товаров?
№ 10. Имеются следующие данные о количестве произведенной продукции и ее себестоимости за три года:
|
Продукция |
Количество продукции, тыс. шт. |
Себестоимость единицы продукции, руб. | ||||
|
1986 г. |
1987 г. |
1988 г. |
1986 г. |
1987 г. |
1988 г. | |
|
А |
120 |
150 |
160 |
10 |
9 |
8 |
|
Б |
10 |
12 |
20 |
63 |
62 |
60 |
В ы ч и с л и т ь: цепные и базисные индексы себестоимости и количества произведенной продукции: а) индивидуальные; б) общие.
П о к а ж и т е взаимосвязь исчисленных индексов.
№ 11. Имеются следующие данные о продаже в городе молока на колхозных рынках и в государственной торговле:
|
|
Средняя цена за литр, коп. |
Продано, тыс. л | ||
|
базисный период |
отчетный период |
базисный период |
отчетный период | |
|
В государственной торговле |
30 |
28 |
400 |
800 |
|
На колхозных рынках |
60 |
50 |
200 |
300 |
Вычислить: 1) индекс цен переменного состава; 2) индекс цен постоянного состава; 3) индекс структурных сдвигов.
Покажите взаимосвязь исчисленных индексов. Поясните полученные результаты индексов.
№ 12. Имеются следующие данные о производстве однородной продукции по двум заводам:
|
Завод |
Выработано продукции «А», тыс. шт. |
Затраты на продукцию, тыс. шт. | ||
|
1985 г. |
1988 г. |
1985 г. |
1988 г. | |
|
№ 1 |
12 |
20 |
48 |
60 |
|
№ 2 |
10 |
17 |
80 |
68 |
Вычислить: 1) индекс себестоимости переменного состава; 2) индекс себестоимости постоянного состава; 3) индекс структурных сдвигов.
Покажите взаимосвязь исчисленных индексов. Поясните полученные результаты.
РЕШЕНИЕ ТИПОВЫХ ЗАДАЧ
№ 1. Имеются данные о продаже товаров на колхозных рынках города в январе месяце:
|
Товар |
Продано товара, тыс. ед. |
Средняя цена единицы товара, руб. | ||
|
1986 г. |
1988 г. |
1986 г. |
1988 г. | |
|
Морковь, кг |
15,0 |
16,2 |
0,8 |
0,7 |
|
Яблоки, кг |
50,0 |
51,0 |
2,5 |
3,5 |
Вычислить: 1) индивидуальные индексы цен и количества проданного товара: 2) общий индекс товарооборота; 3) общий индекс физического объема товарооборота; 4) общий индекс цен и сумму экономии или перерасхода от изменения цен; 5) прирост товарооборота за счет изменения цен и количества продажи товаров.
Покажите взаимосвязь между исчисленными индексами.
Решение. 1. Индивидуальные индексы (однотоварные) равны: а) цен
.
б) количества проданных товаров
.
Так, для моркови
=
0,7:0,8 = 0,875 (87,5%). Следовательно, цена на
морковь снизилась на 12,5%.
= 1,08, т.е. количество
проданной моркови выросло на 8%.
Соответствующие индексы для яблок будут
равны
=
1,4 и
=1,02.
2. Общий индекс товарооборота исчисляется по формуле:
(138,6%).
Товарооборот в январе 1988 г. вырос на 38,6% по сравнению с январем 1986 г.
3. Общий индекс физического объема товарооборота (количества проданных товаров) исчисляется по следующей агрегатной форме индекса:
,
или 102,5%.
Это значит, что количество проданного товара в отчетном периоде было на 2,5% больше, чем в базисном периоде.
4. Общий индекс цен равен:
,
(135,2%),
т.е. цены на оба товара в среднем выросли на 35,2 %.
Экономический
эффект или иначе сумма сэкономленных
или перерасходованных денег за счет
изменения цен исчисляется по данным
общего индекса цен и равна разности
числителя и знаменателя индекса:
тыс.
руб.следовательно,
в связи с ростом цен на 35,2% население в
отчетном периоде дополнительно
израсходовало 49,38 тыс. руб. на покупку
данного товара.
5. Прирост
товарооборота исчисляется как разность
между числителем и знаменателем индекса
товарооборота:
тыс.
руб. Этот прирост обусловлен изменением
цен на товары и изменением количества
проданных товаров. Прирост за счет
изменения цен составил: 189,84-140,46=49,38 тыс.
руб. и за счет изменения количества
проданных товаров: 140,46-137,0=3,46 тыс. руб.
Следовательно, увеличение товарооборота
на 52,84 тыс. произошло за счет роста цен
на 49,38 тыс. руб. и роста количества
проданного товара на 3,46 тыс. руб.
(49,38+3,46=52,84 тыс. руб.).
Между исчисленными индексами существует взаимосвязь:
.
№ 2. Имеются данные о продаже товаров в универсаме города:
|
Товарные группы |
Продано в 1987 г., тыс. руб. |
Индексы количества проданных товаров в 1988 г. к 1987 г., % |
|
Колбасные изделия |
150 |
0,98 |
|
Ткани |
200 |
1,05 |
|
Галантерея |
30 |
1,2 |
(103,4%).
№ 3. Имеются следующие данные о продаже товаров магазина потребительской кооперации за два квартала 1988 г.:
|
Товары |
Товарооборот в действующих ценах , тыс. руб. |
Изменение средних цен во II квартале по сравнению с I кварталом .,% | |
|
I квартал |
II квартал | ||
|
Овощи |
60 |
64 |
-20 |
|
Мясо и мясопродукты |
42 |
44 |
+10 |
|
Зерно |
35 |
38 |
без изменения |
Вычислить: 1) общий индекс товарооборота; 2) общий индекс цен; 3) сумму экономии (или перерасхода), полученную населением от изменения цен; 4) общий индекс физического объема товарооборота.
Решение. Общий индекс товарооборота равен:
(106,6%).
Товарооборот во II квартале вырос по сравнению с первым кварталом на 6,6%.
Общий индекс цен исчислим по формуле среднегармонического индекса, который тождествен агрегатной форме индекса:
.
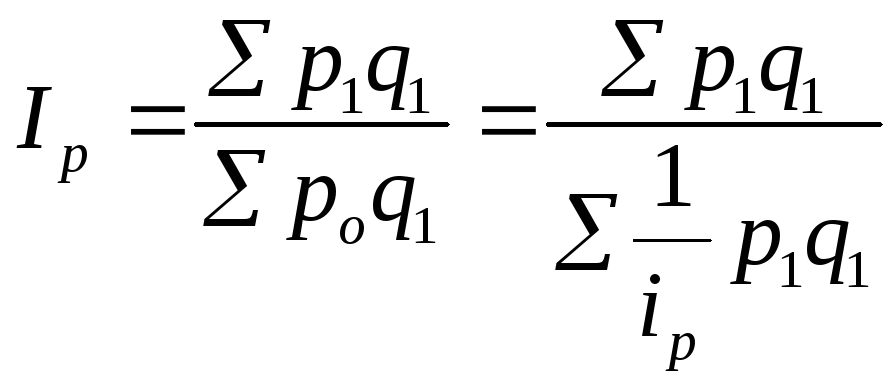Для вычисления этого индекса определим предварительно индивидуальные индексы цен:
для овощей
100-20=80%, или 0,80 в коэффициентах;
мяса и мясопродуктов
100+10=110%, или 1,10 в коэффициентах;
зерна
100%, или 1.
Следовательно,
,
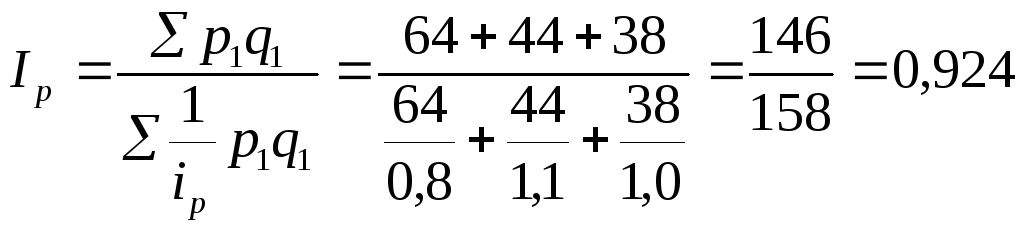или 92,4%, т.е. цены в среднем снизились на 7,6%.
Сумма экономии, полученная населением от снижения цен, составила: 146-158=-12 тыс. руб.
Общий индекс физического объема товарооборота (количества проданного товара) может быть исчислен с помощью взаимосвязи индексов:
Следовательно,
:0,924
= 1,153 (115,3%).
№ 4. Имеются данные о продаже товаров на колхозных рынках города в I квартале 1988 г.:
|
Товар |
Продано, тыс. ед., |
Цена единицы товара, руб., р | ||||
|
январь ( 1 ) |
февраль ( 2 ) |
март ( 3 ) |
январь ( 4 ) |
февраль ( 5 ) |
март ( 6 ) | |
|
Огурцы свежие, кг |
1 |
2 |
3 |
6 |
5 |
4 |
|
Яблоки, кг |
40 |
42 |
30 |
2,5 |
3,0 |
3,3 |
Вычислить : 1) индивидуальные цепные и базисные индексы цен на яблоки; 2) общие цепные и базисные индексы цен и физического объема товарооборота.
Решение. Цепные и базисные индексы цен:
а) цепные
;
;
б) базисные
;
.
Между цепными и базисными индивидуальными индексами существует связь – произведение цепных индексов равно базисному:
Зная базисные индексы, можно вычислить цепные, разделив последующий базисный индекс на предыдущий. Например,
Аналогично исчисляются индивидуальные индексы количества проданных товаров.
2. Исчислим общие индексы цен:
а) цепные
1,162,
или 116,2%.