
- •Практическая работа № 1. Кинетостатический анализ механизмов. Силы, действующие на механизм
- •1. Задачи кинетостатики
- •2. Силы, действующие на механизм
- •3. Определение сил инерции
- •4. Определение сил действующих на механизм двухступенчатого компрессора
- •5. Определение сил действующих на кулачковый механизм
- •6. Задачи для самостоятельной работы
- •1. Методика кинетостатического расчета
- •2. Определение реакций в кинематических парах на примере механизма двухступенчатого компрессора.
- •3. Определение реакций в кинематических парах действующих на кулачковый механизм
- •4. Задачи для самостоятельной работы
- •Практическая работа № 3
- •1. Кинетостатический анализ механизмов с учетом сил трения
- •2. Кинетостатическое исследование механизма двухступенчатого компрессора с учетом сил трения
- •3. Кинетостатическое исследование кулачкового механизма с учетом сил трения
- •4. Задачи для самостоятельной работы.
- •Практическая работа № 4. Уравновешивание механизма
- •1. Уравновешивание вращающихся масс
- •2.Уравновешивание механизмов машины с помощью противовесов на звеньях
- •3. Уравновешивание поступательно-движущихся масс вращающимися противовесами
- •4. Задачи для самостоятельного решения
- •Практическая работа № 7. Расчет маховика

Практическая работа № 7. Расчет маховика
Уравнение движения машинного агрегата может быть представлено в форме дифференциального уравнения
|
|
|
|
Ι |
ϖ |
|
|
|
|
|
|
пр |
|
|
|
|
|
|
||
|
dЕ |
|
d |
|
2 |
|
M Д − M C = |
= |
|
|
|
||
dϕ |
|
dϕ |
|
|||
|
|
|
|
|||
в общем случае, если ω ≠ const и Jпр ≠ const уравнение имеет вид:
M = Iпр dω + dIϕпр ω2 dt d 2
Уравнение движения машины в энергетическом виде |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Ι |
n max |
ω |
2 |
|
|
|
|
|
|
Ι |
n min |
ω |
2 |
|
|
|
|
|
|||||||
|
|
|
|
A = A − A |
= |
|
|
|
max |
− |
|
|
|
min |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
где: Ιn max , Ιn min - моменты инерции механизма приведенные, соответствующие max и min |
|||||||||||||||||||||||||||||||||||
угловой скорости. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ιn max |
= ΙМ + Ιn i max |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
Ιn min |
= ΙМ + Ιn i min |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
A = |
(Ι |
M |
+ Ι |
ni max |
)ω2 |
(1 |
+δ) |
|
|
(Ι |
M |
|
+ Ι |
ni min |
)ω2 (1+δ) |
|
|
|
|
||||||||||||||||
|
|
|
СР |
|
|
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
СР |
|
|
|
|
|||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Решаем уравнение относительно IM , считая, что Ini max и Ini min – незначительными по |
|
||||||||||||||||||||||||||||||||||
сравнению с IM имеем: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ι |
М |
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
δ ω2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
СР |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Пример 1. Определить момент инерции маховика, который надо установить на валу |
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
δ = |
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
50 ; |
|
||
машинного агрегата, чтобы обеспечить коэффициент неравномерности вращения |
|
||||||||||||||||||||||||||||||||||
Движение установившееся, |
ωср =10 |
1/сек; Момент всех приведенных сил |
М = 20 cosϕ |
нм. |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
Приведенный момент инерции постоянный Ιпр = 2 кгм2. |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
а). Дифференциальное уравнение движения для данного случая будет иметь вид |
|
|
|
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
М = Ι |
пр |
|
dω |
|
|
= Ι |
пр |
ε |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
dt |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
Ιпр |
= const |
|
|
dΙпр |
= 0 |
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
т.к. |
|
|
dϕ |
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
б). В положениях, где ω = ωмах , ω = ωмин , ε = 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Угловое ускорение ε = 0 при |
М = 20 cosϕ = 0 , |
|
|
М = 0 при ϕ = π ; ϕ = 3π |
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
Угловая скорость ωа =ωмах |
будет иметь место при |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
ϕа = π2 ; аωб =ωмин - при ϕб |
= 23 π (т.к. до ϕ = π2 |
, |
|
|
|
М ≥ 0 , а от ϕ = π2 |
до ϕ = 32 π , |
М ≤ 0 ). |
|||||||||||||||||||||||||||
73

в). Изменение кинетической энергии после постановки маховика при переходе главного вала из положения, где ωб =ωмин в положении, где ωа =ωмах равно
Eб−а = (Iпра + I м ) |
ωмах2 |
−(Iпрб |
+ I м ) |
ωмин2 |
|
|||||||||||||
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
2 |
|
|
|
|
2 |
|
||||
откуда |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
I м = |
|
2 |
Eб−а − I |
праωмах2 + Iпрбωмин2 |
|
|||||||||||||
|
|
|
|
|
ωмах2 |
−ωмин2 |
; |
|
||||||||||
|
|
|
|
|
|
|
||||||||||||
|
|
Iпра = Iпрб |
= Iпр = const |
|||||||||||||||
|
|
|
ωмах2 |
|
−ωмин2 |
= 2δωср2 |
|
|
|
|
||||||||
|
|
|
|
I м = |
|
2 Eб−а |
− Iпр |
|||||||||||
|
|
|
|
|
|
|
|
|
||||||||||
|
тогда |
|
|
|
|
|
δω2 |
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
ср |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Eб−а = ∫ϕϕа |
|
Mdϕ = 20∫ |
π |
|
|
|
|
|||||||||||
|
32π cos ϕdϕ = 40нм |
|||||||||||||||||
|
|
б |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Iм |
= |
|
40 |
|
|
|
−2 =18кгм2 |
|||||||||||
1 |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
100 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
50 |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Пример 2. Силы и массы машинного агрегата приведены к главному валу. Движение установившееся. Один цикл движения соответствует одному повороту вала. Приведенный момент инерции Iпр = 2 кгм2. Момент приведенных сил сопротивления задан графиком (рис.
1б) Момент приведенных движущих сил постоянный Мдвпр = const , ωcр = 20 1/сек
Определить момент инерции маховика, необходимого для того, чтобы обеспечить заданную величину коэффициента неравномерности δ = 0,025
Решение:
а). Найдем величину момента приведенных движущих сил. При установившемся движении изменение кинетической энергии за цикл равно нулю.
E |
= 0 = Апр − Апр |
1−2 |
дв с |
Работа приведенных движущих сил за цикл
Апрдв = Мпрдв 2π; (Мпрдв = const)
Работа приведенных сил сопротивления за цикл
2π
АпрC = ∫МпрC dϕ
0
Эта работа найдется как площадь треугольника, т.е.
АCпр = |
2∫π МCпрdϕ = 1 |
400π = 200πнм |
|||||
|
0 |
|
2 |
|
|
|
|
т.к. |
E |
= 0 = Апр − Апр |
|||||
1−2 |
|
|
|
дв |
с |
||
|
|
то Апрдв |
|
= Аспр |
|
||
|
|
Мпр = |
Апр |
|
|||
|
|
|
С |
=100 |
|
||
откуда |
|
|
нм |
||||
дв |
|
|
2π |
||||
74

б). Найдем положения, в которых угловая скорость вала будет достигать экстремальных значений.
М = Iпр ε |
ε = |
М |
; |
Iпр ; |
При ωа =ωмах и ωб =ωмин , ε = 0 это будет в положениях «а» и «б», где Мдвпр = МСпр Максимальная угловая скорость в положении «а», т.к. в периоде 1-а движение ускоренное
( Мдвпр ≥ МСпр |
т.е. ε ≥ 0 ). |
|
|
|
в). Определим момент инерции маховика |
|
|
||
|
Eб−а = (Iпра + I м ) |
ωмах2 |
−(Iпрб + I м ) |
ωмин2 |
|
|
|
||
|
2 |
2 |
||
Iпра = Iпрб = Iпр = const
I м = 2 Eб−а − Iпр
откуда δωср2
Eб−а = Адвпр − АСпр = 54 π 100 −π8 100 = 9008 π
M = M (t).
Передаточное отношение редуктора; i12 = 4 , Ι2 =16,0 кгм2, Ι1 =1,00 кгм2, M P = 20000 нм,
M х = 400 нм.
Во время рабочего хода машинного агрегата угловая скорость ротора уменьшается с
величины ωìàõ =148 сек-1 до ωìàõ =130 сек-1. Удержание угловой скорости в заданных пределах обеспечивается установкой маховика 4.
Определить величину момента инерции маховика ΙМ , если механическая характеристика двигателя M дв = а−вω, где а = 30000 нм, в = 200 нм/сек, время рабочего хода tP = 0,3 сек.
1 |
4 |
3 |
2 |
M |
|
|
Mp |
Mx |
|
t |
||
|
||
tp |
tx |
75
Задача 2. Определить величину ΙМ момента инерции маховика, если он должен быть установлен на валу рабочей машины, как это бывает на практике для условий задачи №1. Механическая характеристика двигателя
Mдв = а+вω−сω2
Задача 3. Силы и массы приведены к главному валу. Движение установившееся. Момент сил сопротивления изменяется в соответствии с графиком.
Мпрдв = const , Iпр =10 кгм2, ωср = 30 1/сек
Определить ΙМ , который необходимо установить на главном валу, чтобы обеспечить заданную величину δ =1/ 20 .
пр
Мдв
O
Мспр
М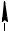
|
|
Мспр |
|
|
нм |
800 нм |
|
О |
4000 |
|
|
/ 2 |
3/ 2 2 |
||
|
|||
|
1циклустанови- |
||
|
вшегосядвижения |
||
76
