Добавил:

ota Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Тольяттинский государственный университет

Предмет:

Геометрия

Файл:

геометрия модуль 3

.pdf

Скачиваний:

Добавлен:

26.07.2016

Размер:

402.34 Кб

Скачать

☆

1 / 31 2 3 > Следующая >>>

Ì3-3

	Содержание Модуля ¹ 3
1. Взаимное пересечение геометрических фигур (общий элемент)........		-1
2.	Решение ГПЗ, когда обе пересекающиеся фигуры занимают
	проецирующее положение. 1 алгоритм....................................................................	-4
3.	Решение ГПЗ, когда одна из пересекающихся фигур
	проецирующая, вторая - непроецирующая. 2 алгоритм.......................	-6
4.	Конические кривые второго порядка....................................................................	-8
5.	Решение ГПЗ, когда обе пересекающиеся фигуры занимают
	непроецирующее положение. 3 алгоритм..........................................................	-17
6.	Частные случаи пересечения поверхностей вращения
	второго порядка...................................................................................................................	-23
7.	Теорема Монжа...................................................................................................................	-24
8.	Контрольные вопросы.......................................................................................................	-25
9.	.Ответы на тест ¹1.................................. .....................................................................	-25
10. Тест ¹1 (позиционные задачи)................................................................................		-26

Ì3-4

МОДУЛЬ ¹3

ПОЗИЦИОННЫЕ ЗАДАЧИ

В данном модуле вы научитесь находить общий элемент пересекающихся геометрических фигур в пространстве, овладеете алгоритмом построения проекций элементов пересечения геометрических фигур, занимающих различное положение относительно плоскостей проекций.

В технике детали большинства изделий имеют формы, представляющие собой поверхности, пересеч¸нные либо плоскостями, либо другими поверхностями. Для того, чтобы проектировать и изготавливать такие изделия, необходимо научиться строить линии пересечения различных геометрических фигур. В этом вам поможет данный раздел начертательной геометрии.

Позиционными задачами называют такие, в которых

определяется взаимное расположение геометрических

фигур в пространстве.

Существует три типа позиционных задач:

1.Взаимный порядок геометрических фигур.

2.Взаимная принадлежность геометрических фигур.

3.Взаимное пересечение геометрических фигур.

Первые две задачи были рассмотрены в предыдущих разделах курса.. Взаимный порядок геометрических фигур - это расположение геометрических фигур относительно плоскостей проекций и наблюдателя: "ближе - дальше", "выше - ниже", "левее - правее" и т.д. Взаимная принадлежность геометрических фигур - это "точка принадлежит ...", "прямая принадлежит ..." и т.д.

Рассмотрим подробнее вс¸ многообразие решений третьего типа задач.

Взаимное пересечение геометрических фигур.

Две геометрические фигуры, пересекаясь, дают общий элемент:

1.Прямая с прямой - точку (а∩b Ê).

2.Прямая с плоскостью - точку (а∩Σ Ê).

3.Прямая с поверхностью - одну или несколько точек (а∩ Ê, Ì ...).

4.Плоскость с плоскостью - прямую линию (Σ∩Ã à).

5.Плоскость с поверхностью - плоскую кривую или плоскую ломаную (Σ∩ ò).

6.Поверхность с поверхностью - пространственную кривую или

несколько пространственных кривых, которые, в свою очередь, могут состоять из плоских кривых или плоских ломаных ( ∩Λ ò).

М3-5 Из всего многообразия этих задач выделяются две общие задачи, которые называют главными

позиционными задачами:

Первая главная позиционная задача (1 ГПЗ) - пересечение линии с поверхностью (первые

три задачи).

Вторая главная позиционная задача (2 ГПЗ) -взаимное пересечение двух поверхностей

(4, 5 и 6 задачи).

При этом следует помнить, что плоскость - это частный случай поверхности, поэтому условимся пересечение плоскостей или плоскости с поверхностью относить ко 2 ГПЗ.

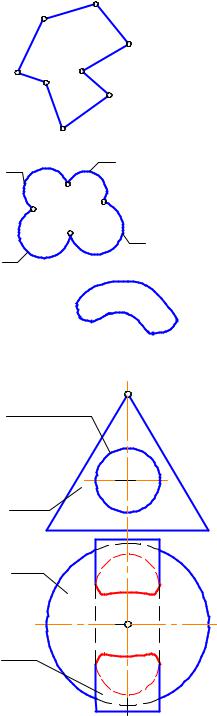
При решении 2 ГПЗ сначала необходимо выяснить, что будет являться общим элементом у двух пересекающихся поверхностей. Чаще всего бывает следующее:

À	Â	а) Пересекаются два многогранника - общий элемент есть пространственная

Ñломаная линия, состоящая из отдельных звеньев (каждое звено -

E		прямая линия), как результат пересечения граней многогранников;
		звенья между собой соединены в точках А, В, С ..., которые
K	D
G		представляют собой точки пересечения р¸бер первого многогранника

F	Ðèñ. 3-1	с гранями второго и наоборот (рис. 3-1).
	n

m		б) Пересекаются многогранник с кривой поверхностью (например, тор с

Â	Ñ	пирамидой). Общий элемент - пространственная кривая линия,
À		состоящая из отдельных звеньев. Каждое звено есть результат
D	k
		пересечения граней многогранника с кривой поверхностью (звенья
l


à)		т, п, k ...- есть плоские кривые). Звенья между собой соединены в
		точках А, В, С, D, которые представляют собой результат пересечения
Ðèñ. 3-2	á)	р¸бер многогранника с кривой поверхностью (рис. 3-2а).
		в) Пересекаются две кривые поверхности (например, сфера с конусом).

2=ò2 =ï2	S2	Общий элемент - пространственная кривая линия (рис. 3-2б).
		Далее необходимо определить количество общих

		элементов пересекающихся поверхностей. Определяется оно
Ô2		в зависимости от характера пересечения поверхностей.
		Характер пересечения поверхностей

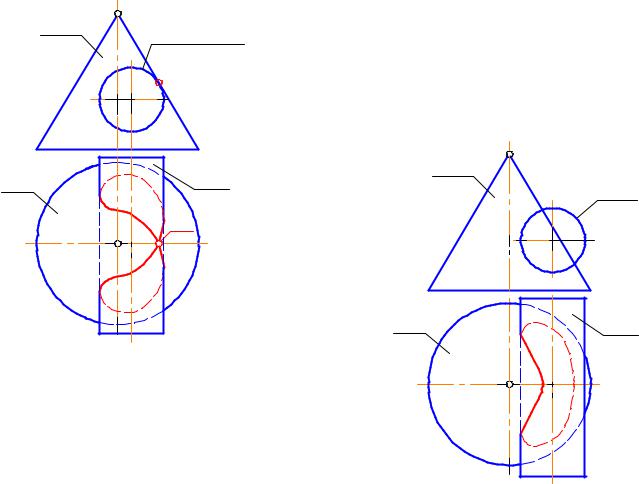
Ô1		Например, пересекаются конус Ф, окружность основания
	ò1	которого параллельна П1 , и фронтально проецирующий

		цилиндр	(ðèñ. 3-3).
	S1
		Такой характер пересечения, когда одна из поверхностей
	ï1
1		насквозь пронзает другую, называется чистое

		проницание. В этом случае линий пересечения две
Ðèñ.3-3		(íà ðèñ. 3-3	ýòî ò è ï).

	S2		Ì3-6
Ô2	S2		Характер пересечения поверхностей, представленный
Ô2	2=ò2	=ï2	на рис. 3-4, когда очерки поверхностей касаются в
	À2		одной точке, является частным случаем
	À2		проницания, когда линий пересечения две (т и п),

но с одной общей точкой ( А ).

			Ô2	S2
Ô1		1	Ô2
Ô1		1		2
ò				2
ò	À1
1	À1
1
S				ò2
1
ï
1
	Ðèñ. 3-4		Ô1	1
Характер пересечения поверхностей, представленный				S1
Характер пересечения поверхностей, представленный
на рис. 3-5, когда одна из поверхностей "вдавливается"				ò1
в другую, называется вмятие. В этом случае линия				ò1
пересечения одна (на рис. 3-5		ýòî - ò).	Ðèñ. 3-5
			Ðèñ. 3-5

Решение главных позиционных задач. 3 случая. 3 алгоритма.

Способ решения главных позиционных задач, или алгоритм решения, зависит от расположения пересекающихся геометрических фигур относительно плоскостей проекций. Здесь имеет место З случая:

- обе пересекающиеся фигуры занимают проецирующее положение. Задачи решаются по первому алгоритму.

- одна из пересекающихся фигур - проецирующая, другая - непроецирующая. Задачи решаются по второму алгоритму.

- обе пересекающиеся фигуры - непроецирующие. Задачи решаются по третьему алгоритму.

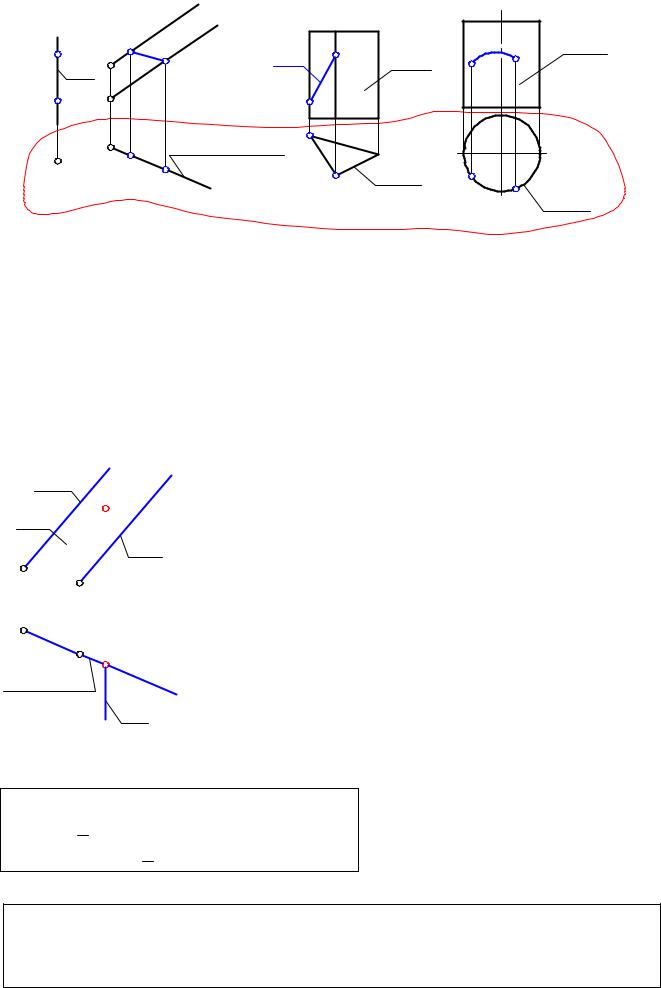
Здесь уместно вспомнить, какие фигуры могут занимать проецирующее положение. Таковыми являются: прямая, плоскость, а из всех известных нам поверхностей проецирующее положение могут занимать только призматическая поверхность (частный случай - призма) и цилиндрическая поверхность (частный случай - прямой круговой цилиндр). На рис. 3-6 показаны примеры горизонтально проецирующих фигур. Напомним, что главными проекциями у них являются: у прямой а - точка а1 , у плоскости Σ- прямая Σ1 , у призмы - треугольник 1

Ì3-7

Â2		k2		c2
		å2		c2
		å2		ï2	2
Ñ2	à2
Ñ2
			Σ1=k1 =c1 =å1		1=ï1
à1 =Â1		=(Ñ1 )			1=ï1
à1 =Â1		=(Ñ1 )		Главные проекции
				Главные проекции

Ðèñ. 3-6

ò2	Γ2
	Γ1=ò1

( а в общем случае - или ломаная линия, или любой многоугольник), у цилиндра Γ - окружность Γ1 (в общем случае - замкнутая или разомкнутая кривая). Напомним также, что главные проекции проецирующих фигур обладают "собирательными" свойствами (рис. 3-6).

Решение задач в случае, когда обе пересекающиеся фигуры занимают проецирующее положение. 1 алгоритм.

Решение рассмотрим на конкретном примере.

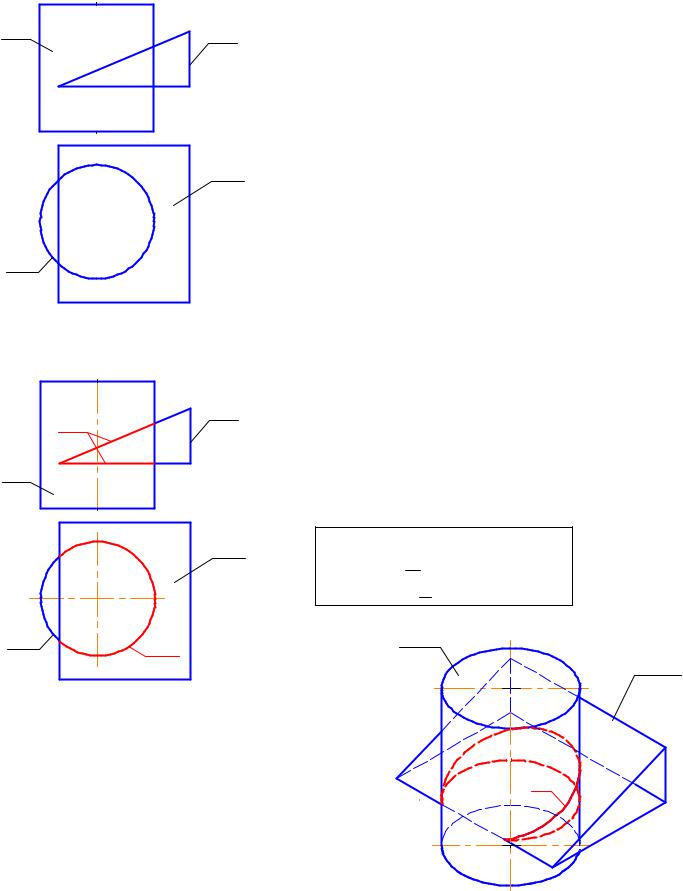
Задача: Найти проекции точки пересечения горизонтально-проецирующей плоскости Σ(т || п) с фронтально-проецирующей прямой а (рис. 3-7).

ò2		à2		=Ê2	Алгоритм: Так как в пересечении участвует прямая линия (а),
	Σ2	à2		=Ê2	то это - первая главная позиционная задача. Обе
	Σ2

				ï2	пересекающиеся фигуры - проецирующие относительно разных
				ï2	плоскостей проекций. Решение начинаем с фронтальной проекции.

					1. Точка К является общим элементом плоскости Σ и прямой а,
					1. Точка К является общим элементом плоскости Σ и прямой а,
					следовательно, К Σ è Ê à. Íî, åñëè Ê à, òî Ê2 à2, а, поскольку
			Ê1		à2 - это точка (главная проекция, обладающая собирательными
Σ1=ò1 =ï1					свойствами), то К2 = à2.
					свойствами), то К2 = à2.
					2. Находим горизонтальную проекцию точки К. Òàê êàê

à1	плоскость Σ íà Ï1	проецируется в прямую линию Σ1 , òî Ê1 , êàê
Ðèñ. 3-7
	общий элемент Σи а, будет располагаться на пересечении Σ1		è à1 .

Выполним краткую алгоритмическую запись вышеизложенного: Σ(ò || ï) ∩ а = К; 1 ГПЗ, 1 алгоритм.

1.Ê à, à || Ï2 Ê2 = à2.

2.Ê à, Ê Σ, Σ || Ï1 Ê1 = Σ1 ∩ à1 .

Таким образом, решение 1 ГПЗ по первому алгоритму заключается в следующем:

Проекции общего элемента на чертеже уже присутствуют. Они совпадают с главными проекциями проецирующих фигур. Решение сводится к их нахождению и обозначению.

М3-8 Вторую главную позиционную задачу решим в соответствии с рассмотренным

алгоритмом.

Задача: найти проекции линии пересечения горизонтально проецирующего цилиндра Ф с фронтально проецирующей призмой Г (рис. 3-8).

Ô2

Алгоритм: Пересекаются две поверхности, это - 2 ГПЗ.

Вначале анализируем, что должно получиться в

результате пересечения. Так как характер пересечения -

вмятие, то общим элементом должна быть одна

пространственная линия - т.

Ã1

Обе фигуры проецирующие относительно разных плоскостей

проекций. Следовательно, согласно 1 алгоритму, проекции

общего элемента должны совпадать с главными проекциями

поверхностей. На фронтальной проекции т2 должна совпадать

Ô1

с Г . Однако, из чертежа (рис. 3-8) видно, что часть главной

проекции призмы Г2 выходит за пределы цилиндра, а это

Ðèñ. 3-8

означает, что совпадение проекции линии пересечения т2 ñ

главной проекцией призмы Г2 только частичное. Следовательно, нужно найти границы общей части. На рис. 3-9 линия т2, совпадающая с Г2 в пределах цилиндра, выделена красным цветом - это

	Ã	фронтальная проекция линии пересечения поверхностей.
	2	Аналогичные рассуждения провед¸м для нахождения
	ò2	Аналогичные рассуждения провед¸м для нахождения
Ô2		горизонтальной проекции линии пересечения т1 . Она совпадает
Ô2		с главной проекцией цилиндра Ф1	в пределах призмы.
		Алгоритмическая запись будет выглядеть следующим образом:
	Ã1	Ô ∩ Г = т; 2 ГПЗ, 1 алгоритм.
		1. ò Ã, Ã \|\| Ï2 ò2 = Ã2.
		2. ò Ô, Ô \|\| Ï1 ò1 = Ô1 .
Ô1	ò1	Ô	Ã
	Ðèñ. 3-9		Ã
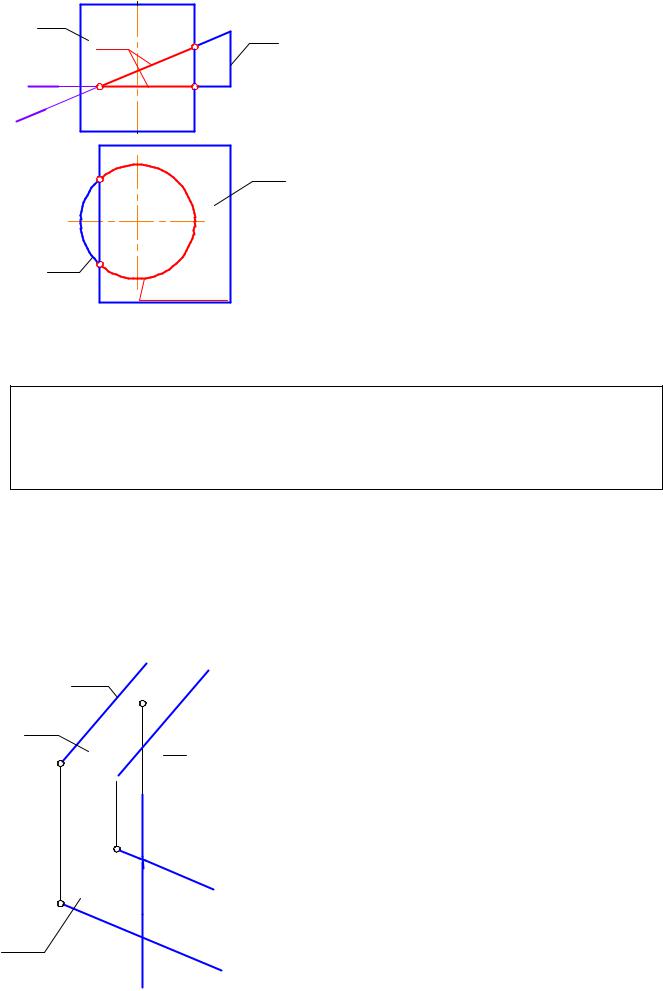
	Проанализируем, из чего состоит линия
пересечения т. Как мы уже предполагали, это			à
пространственная линия. Она состоит из двух			à
плоских кривых а и b (рис. 3-10, 3-11), получающихся			b
от пересечения цилиндра двумя гранями призмы,
которые на рис. 3-11 обозначены плоскостями Σ è Λ.
	Плоскость Λ(Λ2) - это горизонтальная		Ðèñ. 3-10
плоскость уровня. Она параллельна окружности			Ðèñ. 3-10
плоскость уровня. Она параллельна окружности

Ô2			Ì3-9
Ô2	ò	b	Ã2 основания цилиндра, поэтому она пересеч¸т цилиндр
	2	b
Λ2		2	Ф тоже по окружности. Тогда линия а есть дуга
		à2	Ф тоже по окружности. Тогда линия а есть дуга
		à2	окружности, которая спроецируется на П2 â âèäå
2			прямой (а2), à íà Ï1 - в натуральную величину, т.е. в
			прямой (а2), à íà Ï1 - в натуральную величину, т.е. в
			виде дуги окружности (а1 ).
			Плоскость Σ(Σ2) - фронтально проецирующая и
			Ã1
			пересеч¸т цилиндр Ф по эллипсу. Тогда линия b есть
			дуга эллипса, которая спроецируется на П2 â âèäå
Ô1			прямой (b2), à íà Ï1 - в виде дуги окружности (b1 ).
Ô1		m1 (a1 =b1 )	Таким образом, линия пересечения двух заданных
		m1 (a1 =b1 )	поверхностей есть пространственная линия,

	Ðèñ. 3-11	состоящая из двух плоских кривых - дуги окружности
		и дуги эллипса.

	Скорректируем алгоритм решения позиционных задач в 1 случае:

Проекции общего элемента на чертеже уже есть. Они совпадают с главными проекциями проецирующих фигур. Если совпадение только частичное, то находят границы общей части. Решение сводится к их нахождению и обозначению.

Решение задач в случае, когда одна из пересекающихся фигур проецирующая, вторая - непроецирующая. 2 алгоритм.

Решение 1 ГПЗ снова рассмотрим на конкретном примере.

Задача: Найти проекции точки пересечения плоскости общего положения Σ(т || n) с фронтально проецирующей прямой а (рис. 3-12).

Σ2

ò2 à2

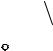ï2

		ï
		1
Σ1	à1	ò
		ò
		1
		1
Ðèñ. 3-12

Графическое условие этой задачи подобно условию 1 ГПЗ , показанному на рис. 3-7. Такая же фронтально проецирующая прямая а пересекается с плоскостью Σ(т || n). Только, в данной задаче плоскость Σ- общего положения. Алгоритм: Решение начинаем, как и в первом случае, с фронтальной проекции. Точно так же, фронтальная проекция точки пересечения К2 совпад¸т с фронтальной проекцией прямой а2, òàê êàê à2 - точка (рис. 3-13).

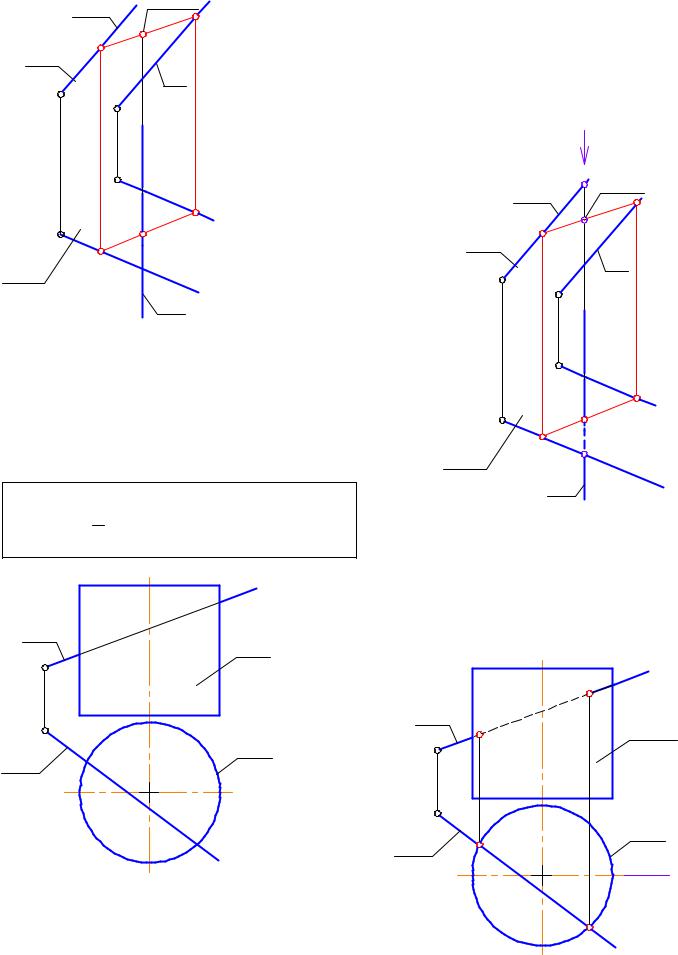
Горизонтальную проекцию точки пересечения К1 найти так однозначно, как в первом случае, уже невозможно. Поэтому будем находить е¸ по признаку принадлежности плоскости Σ. Точка принадлежит плоскости, если она принадлежит прямой, лежащей в этой плоскости. Возьм¸м в плоскости Σлюбую

à =Ê

Ì3-10

ò2

прямую, проходящую через точку К2, например, 1222, íàéä¸ì

2 22

е¸ горизонтальную проекцию 11 21 (1 ò, 2 ï ) è íà ýòîé

Σ2

прямой будет располагаться точка К1 .

ï2

Следующим этапом необходимо определить видимость

прямой а на горизонтальной проекции. Для этого

воспользуемся методом конкурирующих точек (рис. 3-14).

Так как плоскость Σ имеет с

прямой а только одну общую

ò2

à =Ê

точку К, то прямые т и а -

Σ2

скрещивающиеся, а точки3 и 4

на них - горизонтально

ï2

конкурирующие. Пусть точка 3

à1

Ðèñ. 3-13

принадлежит прямой т (то есть

плоскости Σ), точка 4 принадлежит прямой а.. Находим

фронтальные проекции точек. Из чертежа рис. 3-14 видно, что

точка З2 расположена выше, чем точка 42. Следовательно, на

Ê1

данном участке, начиная от точки пересечения К1 , до прямой

3 (4 )

ò1 прямая а1 не видна .

Σ1

Выполним краткую алгоритмическую запись решения:

à1

Σ(ò||n) ∩ a = K; 1 ГПЗ, 2 алгоритм.

1. Ê à, à || Ï2 Ê2 = à2.

Ðèñ. 3-14

2. Ê1 Σ, Ê 12, 12 Σ Ê1

= à1

∩ 11 21 .

Рассмотрим ещ¸ одну задачу: Пересекаются прямая

à2

Ã2

общего положения а с поверхностью горизонтально

проецирующего цилиндра Г (рис. 3-15). Найти проекции

точек пересечения.

à2

Ã1

Ã2

(M2 )

Ðèñ. 3-15

à1

Ã1

Ô1

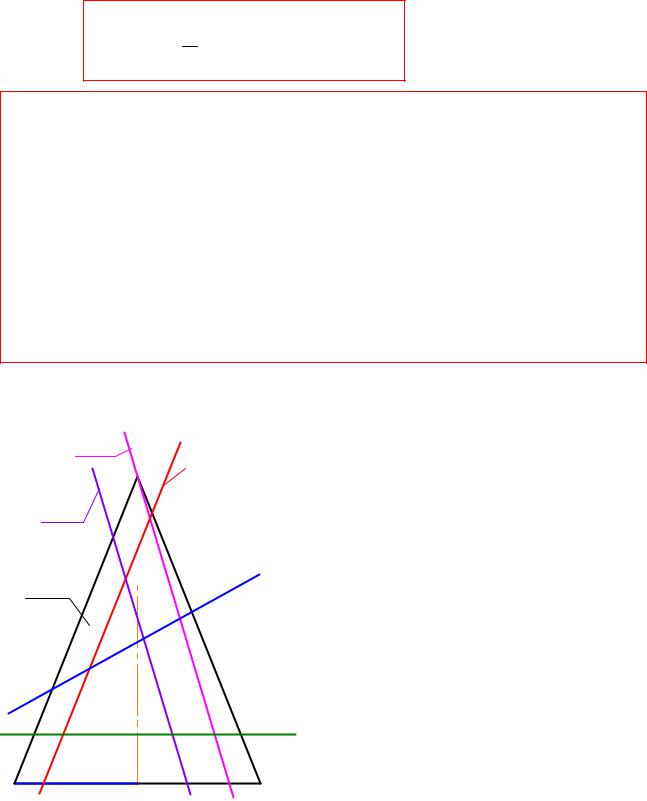
Решение: 1 ГПЗ, 2 алг. Горизонтальная проекция цилиндра -

окружность Г1 , следовательно, в результате пересечения

получаются 2 точки М и N, горизонтальные проекции которых

Ì1 è N1

располагаются на пересечении Г1 è à1 (ðèñ. 3-16).

Ðèñ. 3-16

Ì3-11

Фронтальные проекции точек пересечения М2 è N2 находим по принадлежности прямой а с использованием линии связи. Видимость на П2 определяем по цилиндру: точка N1 расположена перед плоскостью фронтального меридиана Ф, и N2 - видимая; М1 расположена за плоскостью фронтального меридиана Ф, и М2 - невидимая. Часть прямой а между точками М и N находится внутри цилиндра, следовательно, на П2 участок прямой между точками М2 è N2 невидимый. Участок прямой между точкой М2 и очерковой образующей цилиндра l2 также невидим, так как находится за плоскостью фронтального меридиана. Алгоритмическая запись решения:

Ã ∩а = М, N, 1 ГПЗ, 2алгоритм.

1.Ì,N Ã, Ã || Ï1 M1 ,N1 = Ã1 ∩à1 .

2.Ì,N a M2,N2 a2.

Вывод: Решение задач по 2 алгоритму сводится к следующему:

1. Выделяют из двух заданных фигур проецирующую и отмечают

å¸ главную проекцию.

2.Ставят обозначение той проекции искомого общего элемента, которая совпадает с главной проекцией проецирующей фигуры. Если совпадение только частичное, то находят границы общей части.

3.Вторую проекцию общего элемента находят по условию его принадлежности непроецирующей фигуре.

4.Определяют видимость проекций общих элементов и пересекающихся фигур.

Конические сечения

Λ2=à2	=b2	2=ò2
		2=ò2
Σ2=k2		S2
		S2	d2




Ω2

			Φ2
		=

Ã2 =c2

Решение второй главной позиционной задачи

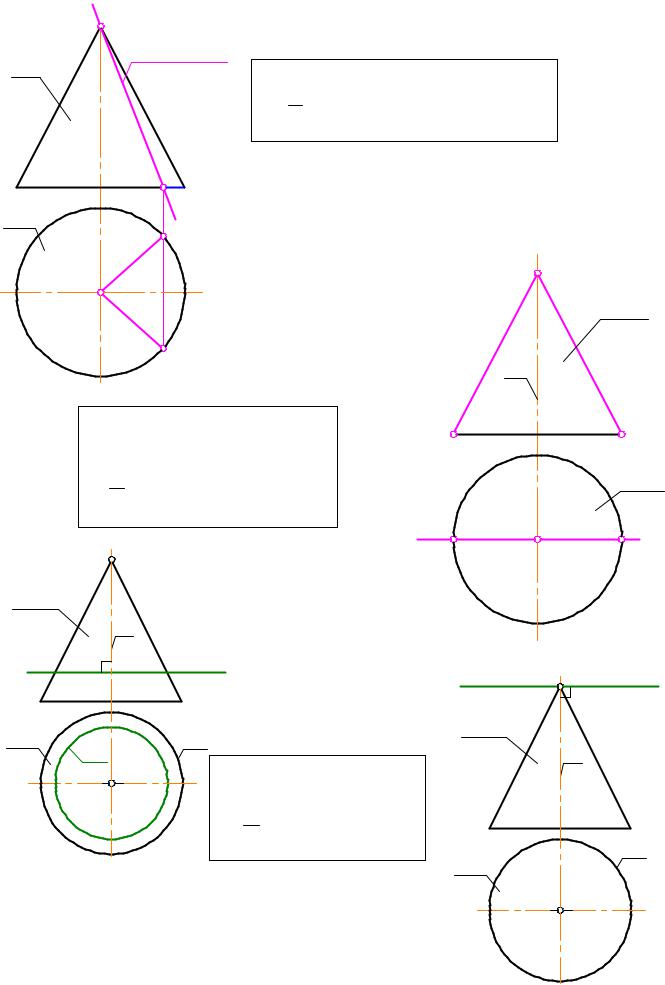
по 2 алгоритму рассмотрим на примере конических сечений. Ещ¸ в Древней Греции был известен тот факт, что при пересечении конуса различными плоскостями можно получить прямые линии, кривые второго порядка и, как вырожденный случай, точку. На рис. 3-17 показана фронтальная проекция конуса Ω2, пересеч¸нного фронтально проецирующими плоскостями Λ2, Ã2, Ô2, 2, Σ2; в сечениях получаются, соответственно, две прямые а и b, окружность c, эллипс d, парабола m и гипербола k.

Рассмотрим каждый случай получения конических Ðèñ. 3-17 сечений, представленных на рис. 3-17, с точки

зрения решения 2 ГПЗ по 2 алгоритму.

			Ì3-12
	S2	Λ2=a2	1. Две образующие получатся в сечении, если плоскость,


			=b2
Ω2			пересекая конус, проходит через его вершину (рис. 3-18).
Ω2			Алгоритм: Ω∩Λ = à,b; 2 ÃÏÇ, 2 àëã.

1.Λ|| Ï2 à2,b2 = Λ2.

2.a1 ,b1 Ω.

Частным случаем такого вида пересечения конуса плоскостью

Ω1		M (N ) является такое положение, при котором плоскость Λ
		2		2	проходит через ось i конуса ( на рис. 3-19				Λ1 совпадает с
		N1			проходит через ось i конуса ( на рис. 3-19				Λ1 совпадает с
	a	N1			плоскостью фронтального меридиана).
	1								S2
	S1			Результатом пересечения являются					S2	Ω2
	b			образующие конуса с максимальным						Ω2
	1			углом между ними (на рис. 3-19
		M1		углом между ними (на рис. 3-19
		M1		это - очерковые образующие				i2
Ðèñ. 3-18				конуса SA и SB).				i2
Ðèñ. 3-18				конуса SA и SB).
	Алгоритм: Ω ∩Λ = SA + SB.						A2			B2
		2 ÃÏÇ, 2 àëã.								Ω1
	1. Λ \|\| Ï S A + S B = Λ .									Ω1
	1	1	1	1	1	1	Λ1
	2. S2A2 + S2B2 Ω.						Λ1
	2. S2A2 + S2B2 Ω.
	S						A1		S1 =i1	B1
Ω2	2			2. Окружность получится в
Ω2				2. Окружность получится в
	i2			сечении, если плоскость, пересекая					Ðèñ. 3-19
	i2	Ã =ñ конус, параллельна окружности							Ðèñ. 3-19
		Ã =ñ конус, параллельна окружности							S2 =Ê2	Ã2
	ï2	2		2 основания п (рис 3-20), а значит,					S2 =Ê2	Ã2
		2		2 основания п (рис 3-20), а значит,
				перпендикулярна оси i конуса .
Ω1	ñ1	ï1					Ω2		i2
Ω1		ï1
				Алгоритм: Г ∩Ω = ñ.
				Алгоритм: Г ∩Ω = ñ.
	S1 =i1			2 ГПЗ, 2 алгоритм.					ï2
	S1 =i1			1. Ã \|\| Ï ñ = Ã .					ï2
					2	2	2			ï1
				2. ñ1		Ω.	Ω1
				2. ñ1		Ω.
	Ðèñ. 3-20							S1 =i1 =Ê1
Вырожденный случай - плоскость Г(Г2) проходит через								S1 =i1 =Ê1
Вырожденный случай - плоскость Г(Г2) проходит через
вершину S конуса Ω(рис. 3-21). Тогда эта плоскость
пересеч¸т конус только в одной точке. Ω∩Ã(Ã2) = Ê.

Ðèñ. 3-21

1 / 31 2 3 > Следующая >>>

Соседние файлы в предмете Геометрия

#
26.07.20161.5 Mб23геометрия метод указания.pdf
#
26.07.2016711.97 Кб16геометрия модуль 2.pdf
#
26.07.2016402.34 Кб12геометрия модуль 3.pdf
#
26.07.2016409.33 Кб11геометрия модуль 4.pdf
#
26.07.2016576.48 Кб37геометрия раб тетрадь.pdf
#
26.07.2016556.58 Кб18геометрия.pdf