
геометрия модуль 2
.pdfÌ2-3
Содержание Модуля ¹2
1. Задание плоскости на комплексном чертеже.................................................... |
4 |
|
2. |
Особые линии плоскости.................................................................................................. |
8 |
3. Прямая, параллельная плоскости............................................................................... |
12 |
|
4. |
Контрольные вопросы. Тест ¹1 (плоскость)................................................. |
16 |
5. Задание поверхности на комплексном чертеже........................................... |
17 |
|
6. |
Задание многогранных поверхностей на чертеже..................................... |
21 |
7. |
Задание кривых линейчатых поверхностей на чертеже........................ |
26 |
8. |
Задание линейчатых поверхностей с плоскостью |
|
|
параллелизма (поверхности Каталана) на чертеже................................. |
29 |
9. |
Задание поверхностей вращения на чертеже.............................................. |
32 |
10. Задание поверхностей вращения второго порядка на чертеже..37
11. Задание поверхностей вращения четвертого порядка (тор) |
|
на чертеже............................................................................................................................ |
41 |
12. Задание винтовых поверхностей (геликоиды) на чертеже............... |
43 |
13. Контрольные вопросы. Тест ¹2 (поверхность). Ответы |
|
на тесты ¹1, 2................................................................................................................. |
46 |
Ì2-4
МОДУЛЬ ¹2
КОМПЛЕКСНЫЙ ЧЕРТ¨Ж ПЛОСКОСТИ
ÈПОВЕРХНОСТИ
Âданном модуле вы познакомитесь с различными видами поверхностей и их модификациями, способами задания их на комплексном чертеже, особенностями построения. Узнаете, что простейшая поверхность - это плоскость.
ЗАДАНИЕ ПЛОСКОСТИ НА КОМПЛЕКСНОМ ЧЕРТЕЖЕ
Поверхность есть то, что имеет только длину и ширину. Евклид "Начала", 4 век до н.э., книга 1, определение 5.
Как вы думаете?
1.Не дана ли в "Началах" трактовка поверхности слишком упрощенно?
2.Какая фигура в современном понимании имеет "только длину и ширину"?
3.Безразмерна ли плоскость, или она имеет границы?
4.Можно ли задать плоскость пространственными линиями?
Плоскость является частным случаем поверхности - это двумерная геометрическая фигура, она имеет только длину и ширину, и не имеет толщины. Обозначается прописными буквами греческого алфавита. Плоскость - это множество точек, но определяется она тремя точками
(напомним, что прямую линию определяют две точки). |
|
||
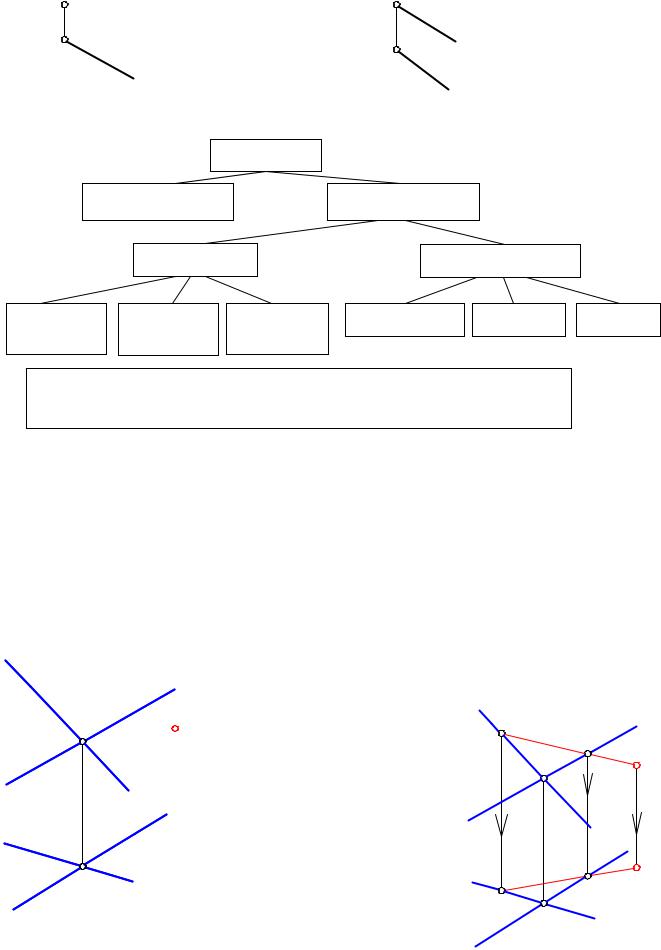
Плоскость можно задать на чертеже: |
|
||
1. Тремя точками: Σ(À,Â,Ñ) |
2. Прямой и точкой, не лежащей на данной прямой: Г(а,В) |
||
À |
Â2 |
à2 |
Â2 |
2 |
Ñ2 |
|
|
|
|
|
|
À |
Â1 |
à1 |
Â1 |
|
|||
1 |
Ñ1 |
|
|
|
|
|
|
3. Двумя параллельными прямыми; 4. Двумя пересекающимися прямыми; 5. Любой плоской фигурой;
(ñ||à) |
à |
Φ(ò∩ï) |
|
Λ(ÀÂÑ) |
Â2 |
ñ2 |
2 |
|
|
|
Ñ2 |
|
ò |
|
À |
||
|
|
2 |
ï2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
ñ |
|
|
|
À1 |
Ñ1 |
1 |
à1 |
|
|
|
|
|
ï1 |
ò1 |
|
|
|
|
|
|
Â1 |
||
|
|
|
|
||
|
|
|
|
|
|
Ì2-5 |
6. Своей главной проекцией: Ω(Ω1 ); |
7. Линией наибольшего наклона плоскости Θ(g1 ,g2 ). |
|
g2 |
Ω1
g1
Ðèñ. 2-1
Плоскости бывают общего и частного положения.
|
|
Плоскость |
|
Общего положения |
|
Частного положения |
|
|
Проецирующие |
Плоскости уровня |
|
Горизонтально |
Фронтально |
Профильно |
Горизонтальная Фронтальная Профильная |
проецирующая |
проецирующая |
проецирующая |
Ðèñ. 2-2 |
|
|
|
|
Если плоскость не перпендикулярна ни одной из плоскостей проекций, то она называется плоскостью общего положения
Примеры чертежа плоскости общего положения см. варианты 1 - 5; 7 (рис. 2-1).
Взаимная принадлежность точки, прямой и плоскости.
Точка принадлежит плоскости, если она принадлежит какой-нибудь
прямой, лежащей в этой плоскости.
Построенние точки в плоскости сводится к двум операциям: построению в плоскости
вспомогательной прямой и построению точки на этой прямой. |
|
|
|
|||
à2 |
b2 |
|
Задача: Плоскость Σ задана пересекающимися прямыми |
|||
|
|
а и b (рис. 2-3). Точка М(М2) принадлежит плоскости. |
||||
|
M |
Найти М1 . |
à2 |
k2 |
|
|
|
|
2 |
Краткая запись условия задачи: |
12 |
22 |
|
|
|
|
||||
|
|
|
Σ(à∩b), Ì(Ì2) Σ; Ì1 = ? |
|
|
|
|
|
Решение: Через точку М2 (ðèñ. 2-4) |
|
|
|
|
|
|
проводим вспомогательную прямую |
|
|
|
|
|
|
k Σ: k2 ∩a2 =12 ; k2 ∩b2 =22 ; |
|
k1 |
2 |
|
|
a1 |
затем находим горизонтальные проекции |
|
1 |
||
b |
1 |
|
a1 |
|||
|
точек 1 и 2 по условию принадлежности |
|
||||
1 |
Ðèñ. 2-3 |
1 |
|
|||
прямым а и b соответственно; через |
|
b1 |
|
|||
|
|
|
Ðèñ. 2-4 |
|||
|
|
|
|
|
||
две точки 11 è 21 проводим прямую k1 è
b2 M2
M1
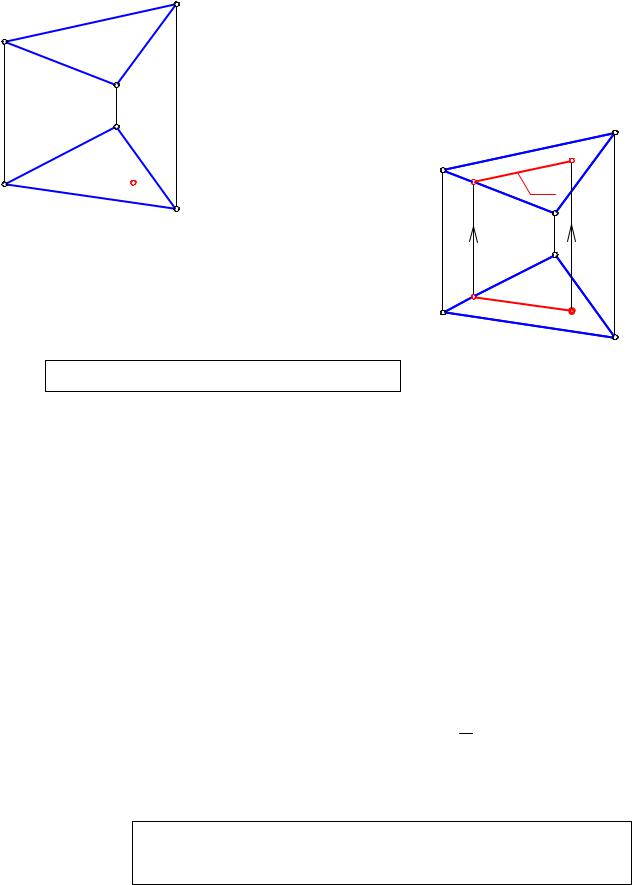
М2-6 на ней, с помощью линии связи, находим точку М1 . И таких прямых можно провести сколько
угодно, то есть, вариантов решения бесчисленное множество.
Прямая принадлежит плоскости, если она:
1.проходит через две точки плоскости;
2.Проходит через одну точку плоскости и параллельна какой-нибудь прямой, лежащей в этой плоскости.
|
Â2 |
В предыдущем примере мы рассмотрели, как построить |
||||
|
À2 |
прямую в плоскости по двум точкам. Для второго случая |
||||
|
|
плоскость Γ зададим треугольником АВС. |
|
|||
|
Ñ2 |
Задача: Плоскость Γ задана АВС(рис. 2-5). |
|
|||
|
Точка М(М1 ) принадлежит Γ. Найти М2 . |
|
Â2 |
|||
|
Ñ1 |
|
||||
|
Ì1 |
Ì(Ì1 ) Γ(ÀÂÑ). Ì2 |
= ? |
|
Ì2 |
|
|
Решение: |
À2 |
|
|||
À1 |
k2 |
|||||
Â1 |
Через точку М1 (ðèñ.2-6) |
12 |
||||
|
|
|||||
|
провед¸м прямую k, |
|
Ñ2 |
|||
|
Ðèñ. 2-5 |
|
|
|||
|
|
параллельную стороне |
|
Ñ1 |
||
|
|
|
|
|
||
треугольника АВ. Она пересеч¸т сторону АС в точке 1: |
11 |
k1 |
Ì1 |
|||
k1 || A1 B1 ; k1 ∩A1 C1 =11 ; с помощью линии связи найд¸м 12 , |
||||||
провед¸м k2 параллельно А2 Â2 и на ней найд¸м точку М2 : |
À1 |
|
Â1 |
|||
Алгоритмическая запись решения: |
|
|
Ðèñ. 2-6 |
|||
11 A1 C1 12 A2 C2 ; k2 12 , k2 || A2 B2 ; M2 k2 . Как вы думаете?
Сколько решений имеет эта задача?
Плоскости частного положения
Плоскости, параллельные или перпендикулярные одной из плоскостей проекций, называются
плоскостями частного положения.
Имеется две группы таких плоскостей: 1. Проецирующие плоскости; 2. Плоскости уровня.
1. Проецирующие плоскости.
Если плоскость перпендикулярна только одной плоскости проекций, то она называется
проецирующей.
Одна из е¸ проекций вырождается в прямую линию, называемую главной проекцией (см. стр. М1-22) и обладающую собирательными свойствами.
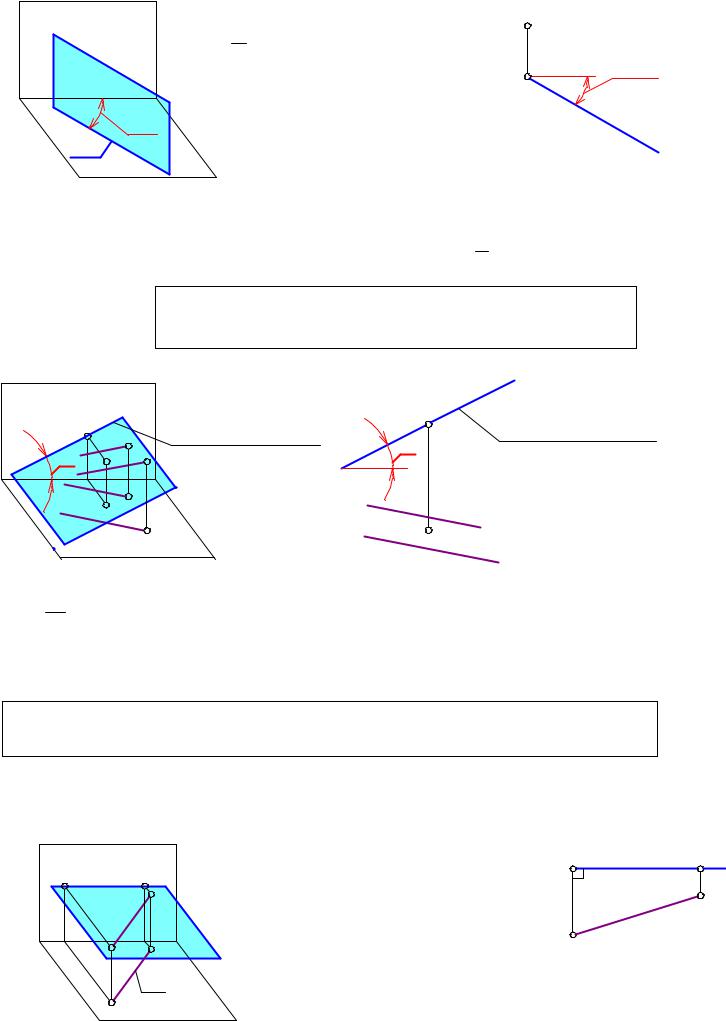
1.1 Горизонтально проецирующая плоскость - это плоскость,
перпендикулярная горизонтальной плоскости проекций: Г|| П1 (рис. 2-7,а - пространственный черт¸ж; рис. 2-7,б - плоский черт¸ж).
Графический признак: Горизонтальная проекция Г1 горизонтально проецирующей плоскости -
прямая линия, не параллельная и не перпендикулярная линиям связи. Это главная проекция .
|
|
Ì2-7 |
|
|
Ï2 |
|
Например: |
|
|
à || Ï1 |
- горизонтально проецирующая |
β |
||
à |
|
плоскость. |
||
à Ï1 |
Ã1 - прямая линия, главная |
|
||
β |
Ã1 |
|||
|
проекция. |
|||
|
|
|
||
à |
β - угол наклона плоскости Г к П2 . |
Ðèñ. 2-7á |
||
1 |
Ï |
|
|
|
|
1 |
|
|
|
Ðèñ. 2-7,à
1.2 Фронтально проецирующая плоскость - это плоскость, перпендикулярная фронтальной плоскости проекций: Σ || Ï2 (рис. 2-8,а - пространственный черт¸ж; рис. 2-8,б - плоский черт¸ж)
Графический признак: Фронтальная проекция Σ2 фронтально проецирующей плоскости -
прямая линия, не параллельная и не перпендикулярная линиям связи. Это главная проекция.
Ï2 |
|
|
|
|
|
M |
|
Σ2= à2 = b2 = M2 |
M2 |
Σ |
|
= à = b = M |
2 |
|
|||
|
α |
|
||||||
à |
|
2 |
2 |
2 |
2 |
|
|
|
α Ì |
b |
|
|
|
||||
|
|
|
|
|
|
|
||
a1 |
|
|
|
|
|
a |
|
|
M1 |
|
|
|
|
|
|
||
|
b1 |
|
|
|
|
M1 |
1 |
|
|
|
|
|
|
b1 |
|
||
|
Ï |
|
|
|
|
|||
|
|
1 |
|
|
|
Ðèñ. 2-8,á |
||
|
|
|
|
|
|
|
||
Ðèñ. 2-8,à |
|
|
|
|
|
|
|
|
Σ(à||b) || Ï2 - фронтально проецирующая плоскость. Σ Ï2 Σ2 |
- главная проекция. |
|||||||
α - угол наклона плоскости Σ ê Ï1 . Прямые а и b Σ à2 ,b2 =Σ2 ; Точка М Σ Ì2 = Σ2 .
2. Плоскости уровня (дважды проецирующие).
Если плоскость перпендикулярна одновременно двум плоскостям проекций, а, следовательно, параллельна третьей, то она называется плоскостью уровня.
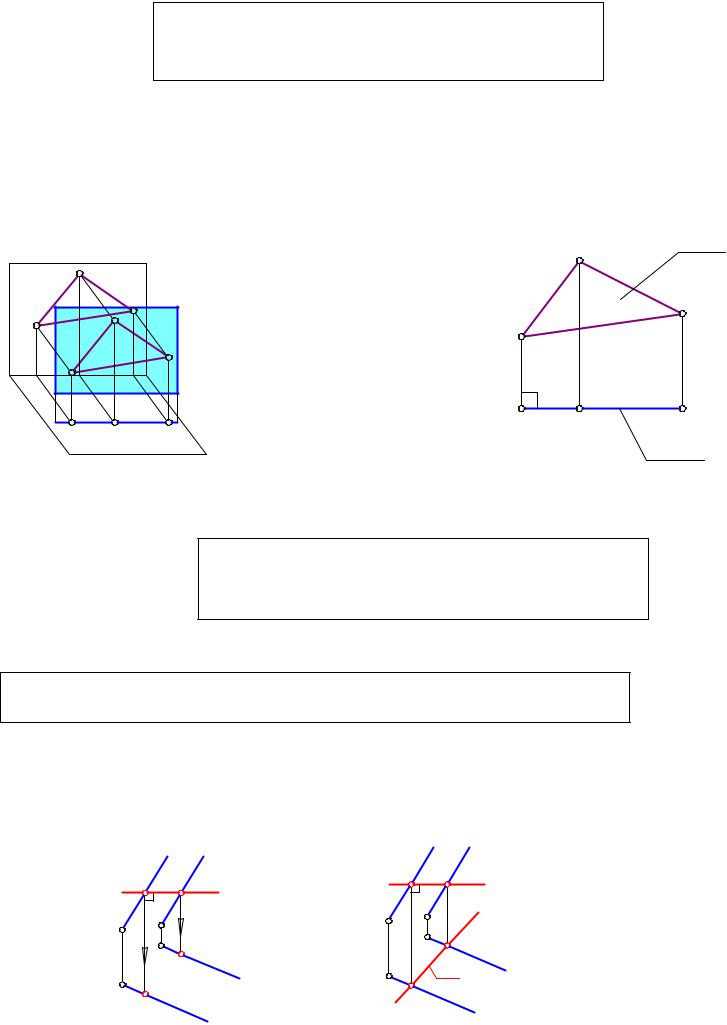
2.1 Горизонтальная плоскость уровня - это плоскость, параллельная горизонтальной плоскости проекций: ||П1 (рис. 2-9,а - пространственный черт¸ж; рис. 2-9,б - плоский черт¸ж).
|
|
|
|
|
|
À2 |
2 |
=ò |
|
À2 |
2=ò2 |
Â2 |
Ï2 |
ÏÏ2 } || Ï1 - горизонтальная |
|
2 |
|||
ò |
|
||||||||
|
|
|
 |
3 |
плоскость уровня. |
1 |
|||
|
|
|
|
|
|
|
|
||
|
ò |
|
|
2 - главная проекция. |
2 À2 À1 . |
|
|
||
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|||
|
À |
|
Â1 |
ò |
ò2 = 2 ; |
À |
Ðèñ. 2-9,á |
||
|
|
ò1 |
1 |
|
|
|
|||
|
|
|| Ï1 |
|ò1 | - натуральная величина т. |
|
|
|
|||
Ðèñ. 2-9,à |
À |
|
|
|
|
|
|||
|
|
1 |
|
|
|
|
|
||
1 |
|
|
Ï |
|
|
|
|
|
|
Â2
Â1
Ì2-8
Графический признак: Фронтальная проекция 2 горизонтальной плоскости уровня - прямая линия, перпендикулярная линиям связи в системе П2 -Ï1 . Это главная проекция.
Так как каждая плоскость уровня параллельна одной из плоскостей проекций, то все плоские фигуры, расположенные на плоскости уровня, проецируются на соответствующую плоскость проекций без искажений.
|
|
2.2 Фронтальная плоскость уровня - это плоскость, |
|
||||
параллельная фронтальной плоскости проекций: Ф||П2 |
(ðèñ. 2-10,à - |
|
|
||||
пространственный черт¸ж; рис. 2-10,б - плоский черт¸ж). |
|
|
|
Φ2 |
|||
|
|
|
Плоскость Φ задана |
|
|
Â2 |
|
Ï |
Â2 |
|
ÀÂÑ, |
|
|
||
Ñ2 |
Φ - фронтальная плоскость |
|
|
Ñ |
|||
2 |
|
|
|
||||
À2 |
|
|
уровня. |
|
À2 |
|
2 |
 |
Ô |
|
|
|
|||
|
|
Φ Ï1 |
|
|
|
|
|
|
À |
|
|
|
|
|
|
|
|
Ñ |
Φ Ï } Φ || Ï2 . |
|
|
|
|
|
|
|
3 |
|
|
|
Ñ |
|
À |
Ô1 |
Φ1 - главная проекция. |
|
|
||
|
1 |
|
Φ1 À2 À1 . |
|
À1 |
 |
1 |
|
Â1 |
Ñ1 |
|
Φ1 |
|||
|
ÀÂÑ Φ À1 Â1 Ñ1 = Ô1 ; |
|
1 |
||||
|
Ï1 |
|
|
Ðèñ. 2-10,á |
|||
|
Ðèñ.2-10,à |
|À2 Â2 Ñ2| - натуральная |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
величина АВС. |
|
|
|
|
|
Графический признак: Горизонтальная проекция Ф1 фронтальной плоскости уровня - |
|
|||||
|
|
прямая |
линия, перпендикулярная линиям связи в системе П1 -Ï2 . |
|
|||
|
|
Это - главная проекция. |
|
|
|
|
|
Особые линии плоскости.
Если прямая принадлежит плоскости и занимает в ней какое-то особое положение, то она называется особой линией плоскости.
К ним относятся линии уровня плоскости: горизонталь. фронталь и профильная прямая, а также
линии наибольшего наклона плоскости.
1. Горизонталь плоскости - это прямая, принадлежащая плоскости, и параллельная горизонтальной плоскости проекций (рис. 2-11.2).
h Ã; h || Ï . |
|
|
22 |
2 |
11 |
2 |
hпринадлежккаТак2. ит |
1 |
урнат-альная |
||
|
|
à2 |
a1 |
hПроводим1. |
иниямрнолдикулясвязи. |
a1 |
тои,оскостплh |
камточумдвпокостивплос |
(1а,2b).hвеличинаh. |
||
Построить |
|
|
b2 |
- н перпе |
|
12 |
2 |
2 |
îäèì íàõ |
|
|
Ã(a || b) |
12 |
h |
|
|
h |
|
|
|
|||
|
|
|
|
|
2 |
|
|
|
|
||
|
|
2 |
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
|
|
21 |
|
|
|
1 |
|
|
|
|
|
|
b1 |
|
|
|
||
|
|
|
1 b1 |
|
|
|
h |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
11 |
Ðèñ. 2-11.à |
|
|
|
Ðèñ. 2-11.á |
|
|
|
||
|
|
|
|
|
|
|
|
|
|||

Ì2-9
Построение горизонтали в плоскости начинают с |
фронтальной проекции h2: она всегда |
|
перпендикулярна линиям |
связи в системе П2 -Ï1 . h1 |
находят по принадлежности плоскости. |
à2 =b2 =Ã2 |
12 =22 =h2 |
21 b1 a1 h1
Ðèñ. 2-12 11
Если плоскость - фронтально проецирующая, то горизонталь такой плоскости - фронтально проецирующая прямая (рис. 2-12).
Ã(a || b) || Ï2 ; h Ã; h || Ï1 .
Так как плоскость Г - фронтально проецирующая, то единственная прямая в такой плоскости, параллельная плоскости проекций П1 - фронтально проецирующая прямая h || П2 .
2. Фронталь плоскости - это прямая, принадлежащая плоскости,
и параллельная фронтальной плоскости проекций (рис. 2-13.2). |
|
fпринадлежакТакк2. ит плоскости, fто |
плоскости(1m,2n). |
|||||
|
|
|
fПроводим1. иниямкулярнолсвязи. |
|
|
|
||
|
|
|
|
|
f2 22 |
|
â |
|
Σ(m ∩ n) |
n2 |
22 |
- перпенди |
n2 |
|
точкам |
|
|
12 |
|
|
12 |
|
|
|
|
|
Построить |
|
m2 |
1 |
|
m2 |
|
вумпод |
|
f Σ; f || Ï2 . |
|
|
|
|
|
|
||
|
|
|
|
|
|
находим |
|
|
|
n1 |
|
m |
n1 |
|
m |
|
|
|
|
21 |
1 |
|
21 |
1 |
|
|
|
11 |
|
11 |
|
|
|
||
|
f1 |
|
f1 |
|
2 |
|
||
|
|
Ðèñ. 2-13.à |
|
|
Ðèñ. 2-13.á |
|
|
|
Построение фронтали в плоскости начинают с горизонтальной проекции f1 : она всегда перпендикулярна линиям связи в системе П2 -Ï1 . f2 находят по принадлежности плоскости. Это - натуральная величина f.
m2 22
n2 12
11 =21 =f1 
 Если плоскость - горизонтально проецирующая, то фронталь f2 такой плоскости - горизонтально проецирующая
Если плоскость - горизонтально проецирующая, то фронталь f2 такой плоскости - горизонтально проецирующая
прямая (рис. 2-14).
Σ1= n1 = ò1
Ðèñ. 2-14
Σ(ò∩ï) || Ï1 ; f Σ; f || Ï2 .
Так как плоскость Σ - горизонтально проецирующая, то единственная прямая в такой плоскости, параллельная плоскости проекций П2 - горизонтально проецирующая прямая f || П1 .
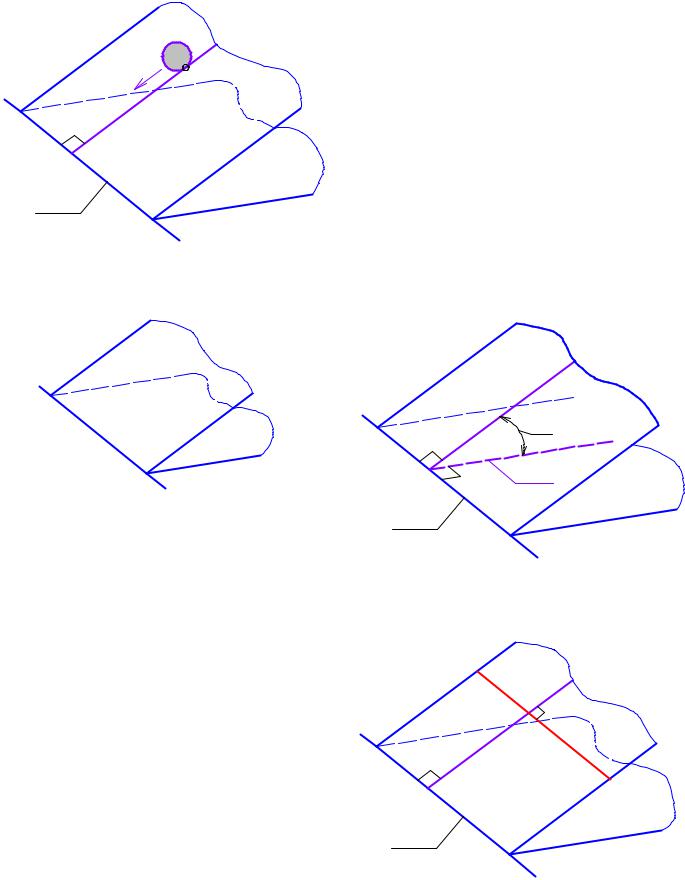
М2-10 4. Линия наибольшего наклона плоскости - это прямая, принадлежащая
плоскости и перпендикулярная одной из линий уровня плоскости.
С е¸ помощью определяют угол наклона заданной плоскости к одной из плоскостей проекций. Условимся линию наибольшего наклона плоскости к П1 обозначать буквой g, к П2 - буквой е.
Ô |
|
|
Линия наибольшего наклона плоскости к |
|
|
|
|
|
À |
|
горизонтальной плоскости проекций называется |
|
|
линией ската (рис. 2-15). Из физики известно, |
|
|
|
|
|
g |
|
|
что шар, выпущенный из руки в точке А, |
|
|
Ï1 |
покатится в плоскости Ф по линии ската g, |
|
|
перпендикулярной т - линии пересечения |
|
|
|
|
|
m |
|
|
плоскостей Ф и П1 . |
|
|
|
|
|
|
Ðèñ. 2-15 |
Рассмотрим подробно построение этой линии |
|
|
|
|
|
|
|
на конкретном примере. |
Задача: Определить угол наклона плоскости Ф к горизонтальной плоскости проекций |
|||
(ðèñ. 2-16). |
|
1. Пространственная модель. |
|
Ô |
|
||
|
|
Ô |
|
Ï1 |
g |
Ðèñ. 2-16 |
|
|
m |
Мерой двугранного угла является линейный угол. |
|
Следовательно, нам нужно определить угол между |
|
прямой g, перпендикулярной m (линии пересечения |
|
плоскостей Ф и П1 ), и е¸ горизонтальной проекцией g1 (ðèñ. 2-17).
. Однако, в плоских чертежах линии пересечения заданных
плоскостей с плоскостями проекций |
|
чаще всего отсутствуют. Поэтому, для построения |
|
линии g в плоскости Ф возьм¸м в этой |
g |
плоскости горизонталь h (рис. 2-18). |
|
Она будет располагаться параллельно m, |
|
òàê êàê |
|
m = Ô ∩ Ï1 , à h || Ï1 . |
m |
Поскольку g m, а h || m, то g h . |
Ðèñ. 2-18 |
|
α 
g1
Ï1
Ðèñ. 2-17
Ô
h
Ï1
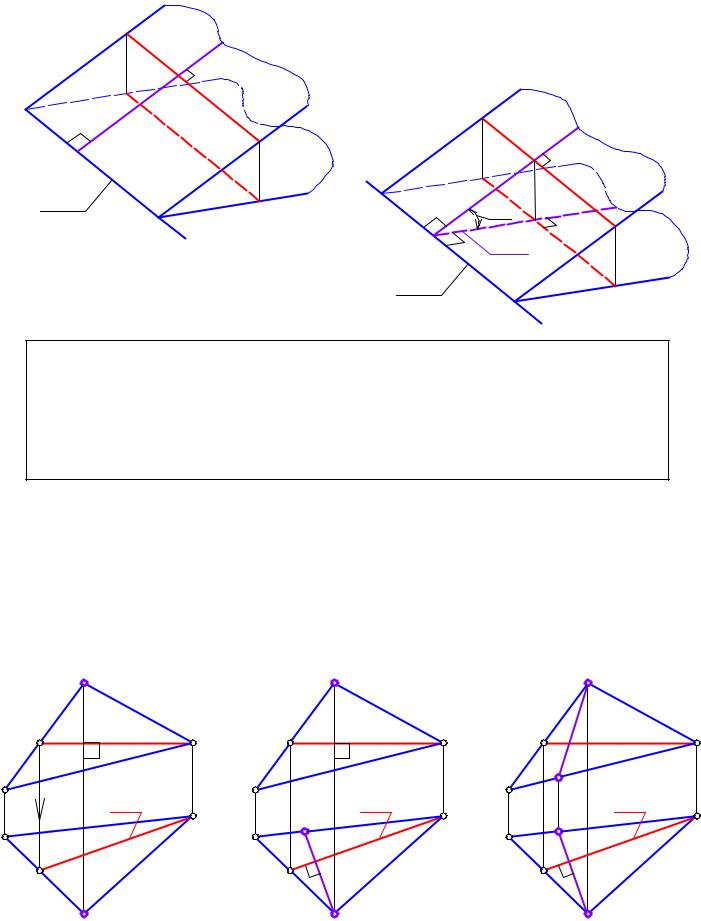
Спроецируем h на П1 , получим h1 (ðèñ. 2-19). Òàê êàê h || m, mo h1 || m1 .
Ô
h
g
h1
Ï1
m
Ðèñ. 2-19
Ì2-11
Согласно теореме о проецировании прямого угла (2 свойство ортогонального проецирования), если g h, mo g1 h1 . Проводим g1 (ðèñ. 2-20). Óãîë αмежду g u g1 - есть угол наклона плоскости Ф к П1 . Ô
h
g α
g1 h1 Ï1
m
Ðèñ. 2-20
Таким образом, угол наклона плоскости к горизонтальной плоскости проекций - это угол между горизонтальной проекцией линии ската этой плоскости и е¸ натуральной величиной.
Выполним алгоритмическую запись вышеизложенного: Ф^Ï1 = g^g1; g h g1 h1.
2. Плоский черт¸ж.
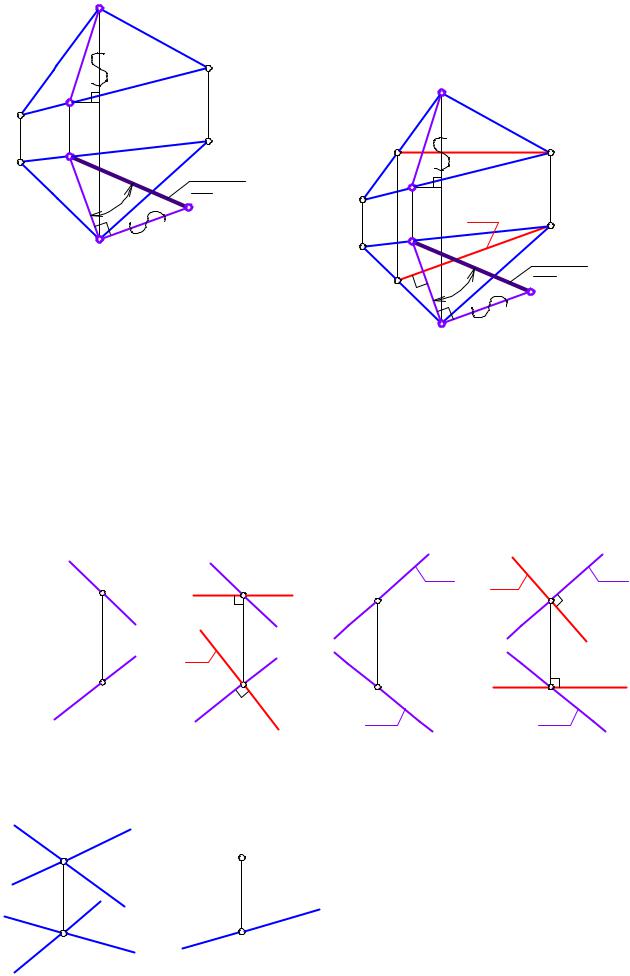
Зададим плоскость Ф треугольником АВС (рис. 2-21).
Алгоритм решения задачи:
1.Проводим в плоскости Ф(АВС) горизонталь h(h2,h1 ).
2.Проводим g1 (B1 K1 ) h1 . Находим g2(B2K2) по принадлежности плоскости.
3.Находим натуральную величину g методом прямоугольного треугольника (рис. 2-21).
|
Â2 |
|
|
|
12 |
h2 |
|
Ñ2 |
12 |
À2 |
|
h1 |
|
À2 |
|
|
Ñ1 |
|
|
|
|
|
|
|
À1 |
|
|
|
À1 |
11 |
|
|
|
11 |
|
Â1 |
Ðèñ. 2-21.1 |
|
|
|
|
|
|
|
Â2 |
|
|
|
h2 |
|
Ñ2 |
12 |
|
h1 |
|
À2 |
Ê1 |
Ñ |
|
|
g1 |
|
1 |
|
|
|
À1 |
|
|
|
|
11 |
Â1 |
Ðèñ. 2-21.2 |
|
|
|
|
|
|
Â2 |
|
|
h2 |
|
Ñ2 |
g2 |
|
|
Ê2 |
h1 |
Ñ1 |
Ê1 |
|
|
g1 |
|
|
Â1 |
Ðèñ. 2-21.3 |
|
|
|
|
|
 |
|
|
|
Ì2-12 |
|
|
|
|
|
|
|
|
|
|
|
4. Óãîë α между g1 |
u g - åñòü óãîë |
|
||||||
|
2 |
|
|
|
наклона плоскости Ф(АВС) к П1 . |
|
|
|||||
|
|
|
|
Ñ2 |
|
|
||||||
|
g2 |
|
|
Полное решение задачи представлено на рис. 2-23. |
||||||||
À |
|
|
|
|
|
|
|
Â2 |
|
|
|
|
2 |
Ê2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ñ1 |
|
|
|
|
h2 |
|
|
|
|
|
Ê1 |
|
|
|
|
12 |
g2 |
|
Ñ2 |
|
||
À1 |
g1 |
α |
|
í. â. g |
|
À2 |
|
|
|
|
||
|
Ê |
|
Ê2 |
h1 |
|
|
||||||
|
|
|
|
|
|
Ñ1 |
|
|||||
|
|
|
|
|
|
|
|
Ê1 |
|
|
||
|
Â1 |
Ðèñ. 2-22 |
|
À |
g1 |
|
|
í. â. g |
|
|||
|
|
|
|
|
|
|
1 |
|
α |
|
Ê |
|
Аналогично можно решить задачу на определение |
|
11 |
|
|
|
|||||||
|
|
|
|
|
||||||||
угла наклона плоскости Ф к П2. Для этого в |
|
|
|
Â1 |
Ðèñ. 2-23 |
|
||||||
плоскости Ф нужно взять фронталь, линию наибольшего |
|
|
||||||||||
|
|
|
|
|||||||||
наклона плоскости к П2 - е строить перпендикулярно |
|
|
|
|
|
|||||||
фронтали ( е2 |
f2 |
→ å1 ) и находить натуральную величину е на П2 . |
|
|
||||||||
После вышесказанного , рассмотрим задание плоскости с помощью линии ската g (рис.2-24а) и |
||||||||||||
линии наибольшего наклона плоскости к П2 - е (рис.2-25а). В первом случае |
при решении |
|||||||||||
конкретных задач к линии ската необходимо добавить горизонталь (h2 линиям связи, h1 g1 ) |
||||||||||||
(рис.2-24б); во втором к линии наибольшего наклона е добавляют фронталь (f1 линиям связи, |
||||||||||||
f2 å2 )(рис. 2-25б). В обоих случаях плоскость получается заданной пересекающимися прямыми. |
||||||||||||
|
g2 |
|
g2 |
h2 |
|
|
|
e2 |
f2 |
|
e2 |
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
h1 |
|
|
|
|
|
|
|
f1 |
|
g1 |
|
|
g1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
e1 |
|
|
|
e1 |
|
||
|
à) |
Ðèñ. 2-24 |
á) |
|
à) |
|
Ðèñ. 2-25 |
á) |
||||
|
|
|
|
|
|
|
|
|
||||
|
|
Прямая, параллельная плоскости. |
|
|||||||||
|
|
|
|
|
Прямая параллельна плоскости, если |
|||||||
b |
|
|
|
K2 |
она параллельна какой-нибудь прямой, |
|||||||
à2 |
|
лежащей в этой плоскости. |
|
|||||||||
2 |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
||
|
|
b1 |
|
m1 |
|
|
Задача: Через точку К(К2 ,Ê1 ) провести |
|||||
a1 |
|
|
|
|
прямую m(m1 ), параллельную плоскости |
|||||||
|
|
K |
|
|
||||||||
|
|
|
|
1 |
|
|
Σ(a ∩ b) (ðèñ. 2-26). |
|
|
|||
|
|
Ðèñ. 2-26 |
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
