2. Точечные оценки параметров распределения выборки

Пусть из генеральной совокупности в результате n испытаний над количественным признаком X извлечена выборка объемом n: варианты x_1, … , x_r и их частоты n₁, … , n_r.

Точечной называют оценку, которая определяется одним числом. Точечные оценки обычно используют в тех случаях, когда число наблюдений велико.

Выборочной средней x_в называют среднее арифметическое значение вариант выборки. Если значения вариант x_1, x₂, … , x_r имеют соответственно частоты n₁, n₂, … , n_r, то

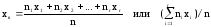. (5)

Выборочной дисперсией D_в называют среднее арифметическое квадратов отклонений вариант x_i от их среднего значения x_в, т.е.

. (6)

Выборочным средним квадратическим отклонением σ_в называют квадратный корень из выборочной дисперсии D_в

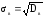. (7)

Исправленную (несмещенную оценку) дисперсию s² выборки получают по формуле

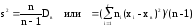. (8)

Аналогично вводится исправленное среднее квадратическое отклонение s

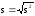. (9)

3. Интервальные оценки параметров распределения выборки

Интервальной называют оценку, которая задается в виде интервала. Интервальные оценки удобно использовать в тех случаях, когда число наблюдений n относительно невелико.

Пусть для неизвестного параметра θ количественного признака X генеральной совокупности статистическими методами найдено значение θ*. Зададимся точностью δ, т.е. | θ - θ* | < δ.

Надежностью оценки неизвестного параметра θ по вычисленному статистическими методами значению θ* называют вероятность γ, с которой выполняется неравенство| θ - θ* | < δ, при этом δ называется точностью оценки. В статистике обычно задаются надежностью γ и определяют точность δ.

Доверительным интервалом для параметра θ называют интервал (θ* - δ, θ* + δ), который покрывает неизвестный параметр θ с вероятностью γ:

P[θ* - δ <X < θ* + δ] = γ.

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение σ неизвестно. Требуется оценить неизвестное математическое ожидание a по результатам выборки с заданной надежностью γ.

Доверительный интервал с уровнем надежности γ для математического ожидания a признака X, распределенного нормально, при неизвестном среднем квадратическом отклонении определяется как

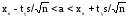, (10)

где x_в – выборочное среднее; s – исправленное среднее квадратическое отклонение выборки; n – объем выборки. Точность оценки δ в этом случае 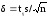. Значениеt_γ = t(γ,n) можно найти из справочной таблицы ”Таблица значений t_γ = t(γ,n)” для распределения Стьюдента.

Доверительный интервал с уровнем надежности γ для среднего квадратического отклонения σ признака X, распределенного нормально, определяется как

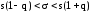, (11)

где s – исправленное среднее квадратическое отклонение выборки; n – объем выборки. Значение q = q(γ,n) можно найти из справочной таблицы ”Таблица значений q = q(γ,n)” для распределения χ².

В случае, когда q >1 доверительный интервал имеет вид

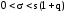. (11') 4. Статистическая проверка статистических гипотез

Статистической называют гипотезу (предположение) о виде неизвестного распределения или о параметрах известного распределения. Основной или нулевой гипотезой H₀ называют выдвинутую гипотезу о неизвестном распределении, вместе с основной H₀ выдвигается и конкурирующая (альтернативная) гипотеза H_1, противоречащая основной.

Основной принцип проверки статистических гипотез состоит в следующем:

в зависимости от вида гипотезы и характера неизвестного распределения вводится функция K, называемая критерием, по значениям ее будет приниматься решение о принятии или отклонении основной гипотезы H₀. Вводится также уровень значимости α как вероятность того, что будет отвергнута верная нулевая гипотеза и принята неверная гипотеза H₁.

Областью принятия гипотезы H₀ называют те значения критерия K, при которых основная гипотеза H₀ принимается, критической областью – отвергается. Для каждой выборки и конкретного вида критерия K по специальным таблицам находятся значения k_кр, называемые критическими точками; критические точки отделяют область принятия гипотезы от критической области. Правосторонней называют критическую область, где K > k_кр, левосторонней K < k_кр и двусторонней (и симметричной) | K| > k_кр.

Пусть из генеральной совокупности в результате n испытаний над количественным признаком X извлечена выборка объемом n: равноотстоящие с шагом h варианты x_1, … , x_r и их частоты n₁, … , n_r. Для нее подсчитаны по формулам (5-9) выборочное среднее x_в и выборочное среднее квадратическое отклонение σ_в.

Для проверки гипотезы о нормальном распределении генеральной совокупности c уровнем значимости α используется критерий χ² Пирсона:

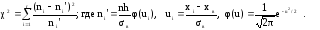(12)

Критическое значение χ²_кр = χ² (α,k) для этого критерия находится из справочной таблицы “Критические точки распределения χ²”. Здесь k = r - 3. Если вычисленное по результатам наблюдений по формуле (12) значение критерия χ²_набл больше χ²_кр, основная гипотеза отвергается, если меньше - нет оснований отвергнуть основную гипотезу.

Если варианты x_1, x₂, … , x_r не являются равноотстоящими или число их сравнительно велико, удобно сгруппировать варианты в отдельные интервалы ( не обязательно равноотстоящие ) [x₁*;x₂*), [x₂*;x₃*), …, [x_m-1*;x_m*). Каждому интервалу назначается представительное значение, равное середине интервала x_i.ср* = (x_i* + x_i-1*)/2 и частота n_i*, равная сумме частот, попавших на интервал. В соответствии с критерием Пирсона, частоты n_i*, попавшие на интервалы [x_i* ; x_i-1*), сравниваются с теоретическими частотами n_i', вычисленными для соответствующих интервалов нормальной случайной величины Z с нулевым математическим ожиданием и единичным средним квадратическим отклонением (Z принадлежит N(0,1)).

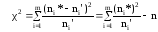, (13)

n_i' = nP_i, где n - обьем выборки;

P_i = Ф(z_i+1) – Ф(z_i), вероятности попадания X на интервал (x_i*,x_i+1*) или

Z на (z_i,z_i+1);

z_i = (x_{i ср}*–x_в*) / σ*; i = 2,3,..,m-1; крайние интервалы открываем z₁ = –∞,

z_m = ∞, а Ф(z_i) – значение функции Лапласа.

Критическое значение χ²_кр = χ² (α,k) для этого критерия находится из справочной таблицы “Критические точки распределения χ²”. Здесь k = m – 3. Если вычисленное по результатам наблюдений по формуле (13) значение критерия χ²_набл меньше χ²_кр, нет оснований отвергнуть основную гипотезу, если больше – основная гипотеза не принимается.

Для проверки гипотез о дисперсии σ² генеральной совокупности с нормальным законом распределения при заданном уровне значимости α используется критерий

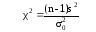, (14)

где s² – исправленная дисперсия выборки; n – объем выборки; σ₀² – гипотетическое значение дисперсии.

А) Пусть выдвинута нулевая гипотеза H₀: σ² = σ₀² о равенстве неизвестной генеральной дисперсии σ² предполагаемому значению σ₀² при конкурирующей гипотезе H₁: σ² ≠ σ₀². Для проверки этой гипотезы по результатам выборки вычисляется значение критерия (14) χ²_выб. Затем по таблице «Критические точки распределения χ²», по заданному уровню значимости α и числу степеней свободы k = n – 1 находятся левое критическое значение χ²_лев.кр(1 – α/2;k) и правое критическое значение χ²_{прав.кр}(α/2;k). Если при этом χ²_лев.кр < χ²_выб < χ²_{прав.кр}, нет оснований отвергнуть основную гипотезу, конкурирующая – отвергается. В противном случае принимается конкурирующая гипотеза и отвергается основная.

Б) Пусть теперь выдвинута нулевая гипотеза H₀: σ² = σ₀² о равенстве неизвестной генеральной дисперсии σ² предполагаемому значению σ₀² при конкурирующей гипотезе H₁: σ² > σ₀². Для проверки этой гипотезы по результатам выборки вычисляется значение критерия (14) χ²_выб. Затем по таблице «Критические точки распределения χ²», по заданному уровню значимости α и числу степеней свободы k = n – 1 находится критическое значение χ²_кр( α;k). Если при этом χ²_выб < χ²_кр, нет оснований отвергнуть основную гипотезу, а конкурирующая – отвергается.

В) Пусть теперь выдвинута нулевая гипотеза H₀: σ² = σ₀² о равенстве неизвестной генеральной дисперсии σ² предполагаемому значению σ₀² при конкурирующей гипотезе H₁: σ² < σ₀². Для проверки этой гипотезы по результатам выборки вычисляется значение критерия (14) χ²_выб. Затем по таблице «Критические точки распределения χ²», по заданному уровню значимости α и числу степеней свободы k = n – 1 находится критическое значение χ²_кр( 1- α;k). Если при этом χ²_выб > χ²_кр, нет оснований отвергнуть основную гипотезу, конкурирующая – отвергается.

Для проверки гипотез неизвестной средней a генеральной совокупности с нормальным законом распределения с неизвестной дисперсией при заданном уровне значимости α используется критерий Стьюдента

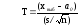, (15)

где x_выб – выборочное среднее; a₀ гипотетическое значение средней; n – объем выборки; s – исправленное среднее квадратическое отклонение.

А) Пусть выдвинута нулевая гипотеза H₀: a = a₀ о равенстве неизвестной генеральной средней a предполагаемому значению a₀ при конкурирующей гипотезе H₁: a ≠ a₀ . Для проверки этой гипотезы по результатам выборки вычисляется значение критерия (15) T_выб. Затем по таблице «Критические точки распределения Стьюдента», по заданному уровню значимости α и числу степеней свободы k = n – 1 находится двустороннее критическое значение T_{двустор.кр}(α;k). Если при этом | T_выб | < T_{двустор.кр}, нет оснований отвергнуть основную гипотезу, а конкурирующая – отвергается.

Б) Пусть теперь выдвинута нулевая гипотеза H₀: a = a₀ о равенстве неизвестной генеральной средней a предполагаемому значению a₀ при конкурирующей гипотезе H₁: a > a₀ . Для проверки этой гипотезы по результатам выборки вычисляется значение критерия (15) T_выб. Затем по таблице «Критические точки распределения Стьюдента», по заданному уровню значимости α и числу степеней свободы k = n – 1 находится критическое значение T_{правостор.кр}(α;k). Если при этом T_выб < T_{правостор.кр}, нет оснований отвергнуть основную гипотезу , а конкурирующая – отвергается.

В) Пусть теперь выдвинута нулевая гипотеза H₀: a = a₀ о равенстве неизвестной генеральной средней a предполагаемому значению a₀ при конкурирующей гипотезе H₁: a < a₀ . Для проверки этой гипотезы по результатам выборки вычисляется значение критерия (15) T_выб. Затем по таблице «Критические точки распределения Стьюдента», по заданному уровню значимости α и числу степеней свободы k = n – 1 находится критическое значение T_{правостор.кр}(α;k) и полагают T_{левостор.кр} = –T_{правостор.кр}. Если при этом T_выб > T_{левостор.кр}, нет оснований отвергнуть основную гипотезу, а конкурирующая – отвергается.