1.4 Ориентирование линий

Ориентированием называется определение направления относительно исходного. За исходные направления принимают истинный (географический), магнитный и осевой (ось х ) меридианы. Углы, отсчитанные от северных направлений истинного и магнитного меридианов называются соответственноистинными (географическими) А_ИСТ и магнитными А_М азимутами, а от осевого меридиана (или от оси х )– дирекционными углами .Азимуты и дирекционные углы отсчитываются по часовой стрелке от 0⁰до 360⁰. Для перевычисления из одной системы в другую строится график ориентирных углов для каждого конкретного случая (рис. 1.7).

Магнитное склонение  и сближение меридиановмогут быть восточными (со знаком плюс) или западными (со знаком минус). И тогда общая формула связи :

А_ИСТ = А_М +  =  + . (1.4)

 и подписаны на каждом листе карты

1-2-заданное направление; С, N, +Х -направления истинного, магнитного и осевого меридианов;  - дирекционный угол; А_ист – истинный азимут; А_М – магнитный азимут;  - магнитное склонение;  -сближение меридианов

Рис. 1.7 - График ориентирных углов

П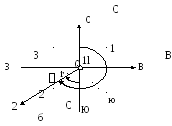ри решении некоторых задач используютсярумбы. Румбомrназывают острый угол, отсчитанный от ближайшего конца исходного направления. Румбические четверти : северо-восток, юго-восток, юго-запад, северо-запад, сокращено СВ, ЮВ, ЮЗ, СЗ. Записывают румбы следующим образом:r = ЮВ: 34⁰ 45'(читается: от южного конца меридиана к востоку на34⁰ 45'). На рис. 1.8 приведена схема перехода от румба к дирекционному углу и обратно.

Рис. 1.8 - Зависимость между румбами и дирекционными углами

Если на рис.1.8, а r = ЮВ: 34⁰ 45', то = 180⁰ – r = 145⁰ 15'; если на рис.1.8, б = 214⁰ 45', тоr = ЮЗ: ( - 180⁰) =ЮЗ: 34⁰ 15' . Каждой румбической четверти соответствует своя формула связи. При решении подобных задач следует составлять схему аналогично рис. 1.8.

Если _1-2 - дирекционный угол линии 1-2, называемыйпрямым, а_2-1–обратным, то очевидна связь между ними:

_2-1 = _1-2 + 180⁰.(1.5)

Вследствие этого решение всех плановых задач ведется в системе дирекционных углов.

Вследствие того, что меридианы сходятся в полюсах, азимуты одной и той же линии различны в разных ее точках. Дирекционные же углы в разных точках линии одинаковы, так как они отсчитываются от параллельных осевому меридиану линий (рис.1.9).

5. Решение основных плановых задач

Вычисление дирекционных углов смежных сторон. Постановка задачи: по заданному дирекционному углу начальной стороны и измеренным горизонтальным углам вычислить дирекционные углы последующих сторон. Если известен дирекционный угол_1-2линии1-2и измерен горизонтальный угол₂(правый по ходу). то дирекционный угол_2-3смежной стороны будет равен (рис. 1.10) :

_2-3=_2-1-₂- (1.6)

дирекционный угол последующей линии равен обратному дирекционному углу предыдущей линии минус горизонтальный угол правый по ходу. С учетом (1.5) получим формулу

_2-3=_1-2+ 180⁰-₂(1.7)

Рис.1.10 - Связь между дирекционными и горизонтальными углами

Применяя формулу (1.7) дальше по ходу, получим цепочку вычислений дирекционных углов последующих сторон.

В точке 2 можно измерить либо угол правый по ходу, либо угол’левый по ходу (рис.1.11). Связь междуи’ очевидна:

 + ’ = 360⁰.(1.8)

Направление хода

Подставив (1.8) в (1.7) , получим

_2-3 = _1-2 + 180⁰ + ₂′ (1.9)

В основном при вычислении дирекционных углов применяют формулу (1.7).

Прямая геодезическая задача. Задача заключается в определении координат конечной точки линии по заданным координатам начальной точки, дирекционному углу (или румбу) и длине линии на горизонтальной плоскости.

В

Дано: х₁иу₁ ;_1-2иd. Определить х₂иу_2. Катетыx_1-2иу_1-2 , называемымиприращениями координат:

х_1-2 = d Cos _1-2 ,

у_1-2 = d Sin _1-2 . (1.10)

При вычислениях на МК знаки х иу зависят от дирекционных углов (от 0⁰до 360⁰). Определяются автоматически. И тогда

х₂ = х₁ + х_1-2 ,

у₂ = у₁ + у_1-2. (1.11)

основу положено решение прямоугольного треугольника по формулам тригонометрии (рис.1.12).

Рис.1.12 - Прямая и обратная

геодезическая задача

Вычисления приращений координат можно выполнить через румбы:

х_1-2 =  d Cos r , y_1-2= d Sin r (1.12)

Знаки приращений определяются по названию румба (рис. 1.13).

Рис.1.13 – Знаки приращений в румбических четвертях

Обратная геодезическая задача. Задача заключается в определении дирекционного угла и длины линии по известным координатам начала и конца линии.

Дано: х₁ и у₁,х₂ и у₂. Определить_1-2 и d. Решение на основании формул (1.11) и (1.12):

х_1-2 = х₂ – х₁ ; у_1-2 = у₂ - у₁ ; r = arc tg (y_1-2 / x_1-2);(1.13)

название румба определяется по знакам х и усогласно рис.1.13; по румбу вычисляется дирекционный угол по правилам рис.1.8;

d = x / cos r = y / sin r . (1.14)