1. 3 Системы координат и высот, применяемые в геодезии

Для определения положения точек на земной поверхности в геодезии применяются системы координат: географическая, прямоугольная, полярная.

Система географических координат. В этой системе Землю принимают за шар, а за координатные оси – географические (истинные) меридианы и параллели. Начало координат – пересечениеГринвичского меридиана, принимаемого за ноль, с экватором. Точка на поверхности шара определяется географической широтойВи географической долготойL. ( Долгота 0⁰– центр зала Гринвичской обсерватории вблизи Лондона). Географические координаты подписаны в углах топографических карт. Широту и долготу точки по карте можно определить, используя минутные деления рамок карты.

Система плоских прямоугольных координатприменяется на небольших участках, принимаемых за плоскость. Ось Х – северное направление меридиана, ось У – восточное направление горизонтальной линии (рис.1.3).

В строительстве эта система применяется для составления планов небольших участков Начало координат т. О выбирается с таким расчетом, чтобы на всем плане не было отрицательных координат (план должен располагаться в северо-восточной части). Такая система плоских прямоугольных координат называется частной (илиместной).

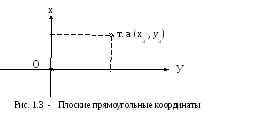
При выполнении геодезических работ, носящих местный характер (съемочные работы способом прямоугольных координат, составление планов архитектурных ансамблей, архитектурные обмеры зданий, памятников архитектуры, составление разбивочных планов и планов вертикальной планировки и т. д.), принимают частную систему координат, в которой начало координат и направление осей выбирают произвольно, исходя из удобства их использования.

АА

Полярную систему координат можно успешно применять при архитектурных обмерах. С одной станции измеряются полярные углы угломерными приборами – теодолитамии полярные расстояниярулеткой.

План можно составит по полярным координатам при помощи транспортира и линейки. А можно полярные координаты

Система полярных координат. В строительстве эта система (рис.1.4) применяется при съемочных работах. За полюсОпринимают точку местности, за полярную осьОА- любое направление на местности; т.Мбудет описываться координатами: полярным углом, измеренным от полярной оси по часовой стрелке, и полярным расстояниемd. ТочкуМлегко построить на плане при помощи транспортира и линейки.

и

щО

мМ

тd

Рис 1.4 - Система полярных координат

пере вычислить в прямоугольные координаты и по ним составить план, что будет точнее, чем при помощи транспортира.

Система координат Гаусса - Крюгера. Система применяется для изображения на плоскости значительных частей земной поверхности с учетом кривизны Земли в картографической проекции Гаусса. Для этой цели земную поверхность делят с севера на юг на узкие ленты –зонышириной 6⁰. На экваторе ширина зоны около 667 км, к северу – уменьшается. Счет зон от Гринвичского меридиана на восток. Средний меридиан зоны называетсяосевым, долготу его L₀можно подсчитать по формуле

L₀ = 6 n – 3⁰ ,(1.1)

где n- номер зоны.

Каждая зона (от 1 до 60) в отдельности проектируется на плоскость при условии равенства углов на сфере и на плоскости. Такая проекция называетсяравноугольнойи обеспечивает подобие контуров на сфере и на плоскости, что удобно при решении задач в строительстве. При развертывании зоны в плоскость экватор и осевой меридиан изображаются прямыми линиями, которые принимаются за координатные оси:ось х – северное направлениеосевого меридиана, ось у – восточное направление экватора(рис.1.5). Точка на местности обозначается координатами:n, x, y– номер зоны, расстояния от экватора и осевого меридиана. Например, т.В: зона 3,х=6021550 м, у=- 205675 м. Такая система называетсядействительнойсистемой координат. В действительной системе точки к востоку от осевого меридиана зоны имеют положительные ординаты, к западу - отрицательные

Для удобства чтения все ординаты на картах увеличены на 500 км. Связь между измененными ординатами и действительными:

у' = y + 500 000 м. (1.2)

Перед измененной ординатой пишется номер зоны. Такие ординаты называются преобразованными.Например, по карте определилит В: х = 6021550 м, у(преобр.) = 3294325м. Следовательно, зона 3, действительная ордината в соответствии с (1.2)у=-205675м. Или,у (пр.)=32675450 м, что соответствует зоне 32, расстоянию от осевого меридиана зоныу = + 175450 м.

Для удобства определения координат точек на планах и картах строят координатные сетки - линии параллельные координатным осям. На картах они кратны км (километровая сетка). На планах проводятся через 10 см. При решении задач по определению координат точек по картам и планам измерения ведутся циркулем-измерителем до 0.2 мм от двух координатных линий сетки. За окончательный результат берут среднее. Измерения от двух линий, как для х так и для у повышают точность измерений, компенсируют деформацию бумаги, выявляют грубые ошибки.

Если в проекции Гаусса горизонтальные углы на сфере и на плоскости равны, то длины линий искажаются по мере удаления от среднего меридиана зоны к краям зоны. (При развертывании зоны в плоскость она расширяется). На краях 6-градусных зон искажения в длинах линий достигают 1/1500. Этой точности достаточно при решении задач технической точности. При необходимости повысить точность решения задач применяют 3-градусные зоны. На краях таких зон искажения в длинах линий не превышают 1/6000. Трехградусные зоны применяют при картографировании городских территорий.

Системы высот. Высоты, отсчитанные от уровенной поверхности моря (поверхности геоида), называютсяабсолютными. В нашей стране за абсолютный нуль принят многолетний средний уровень Балтийского моря (рис1.6) Такая система высот называетсяБалтийской. Разность высот точек называетсяпревышением.

h_АВ = Н_В – Н_А - (1.3)

п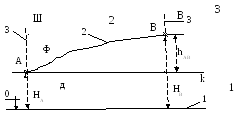ревышение по линииАВ. Превышение по линииВА (обратное)h_ВА = Н_А -Н_В ; очевидно, чтоh_ВА = - h_АВ.

1-уровенная поверхность Балтийского моря; 2–физическая земная поверхность; 3–отвесные линии; Н_А, Н_В–высоты в Балтийской системе; h_АВ–превышение точки В над точкой А

Рис.1.6 - Системы высот

Высоты, отсчитанные от произвольной уровенной поверхности, называются условными(илиотносительными). Такую систему высот принято называтьчастной(илиместной). В строительстве преимущественно применяется частная система высот. Так при возведении отдельных зданий и сооружений за нуль высот принимают верхнюю поверхность пола первого этажа жилого дома или пола цеха промышленного предприятия. Эту отметку выносят на цоколь здания и от нее ведут отсчет: вверх - с плюсом, вниз - с минусом. Численное значение высоты называетсяотметкой.

Частная система высот применяется при архитектурных обмерах, составлении планов архитектурных ансамблей, планов вертикальной планировки внутриквартальных городских территорий и под строительство отдельных зданий, планов вертикальной планировки городских улиц и дорог.