26. Динамические характеристики средств измерений: Дифференциальные уравнения, передаточные функции.

Дифференциальнное уравнение. Динамический режим широкого класса измерений может быть описан линейным дифференциальным уравнением с постоянными коэффициентами

где i, l—порядок производных от x(t)_изм и x(t)_ист;A_i,B_l –коэффициенты.

В статическом режиме при x_ист =const, x _изм = const уравнение вырождается в x_изм=Kx_ист, где К = В_о/А_о—номинальный коэффициент преобразования средства измерений.

Решение дифференциального уравнения позволяет оценить динамическую погрешность и получить исправленный результат измерения, если известны коэффициенты А_i и В_l.

Передаточная функция. Выразив входящие в дифференциальное уравнение x(t)_ист и x(t)_изм в операторной форме, запишем уравнение в виде

,

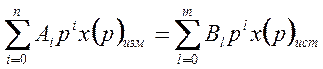где р - оператор дифференцирования d/dt.

Передаточной функцией W(p) называют отношение изображения выходной величины динамической системы к изображению входной величины

Как правило, передаточные функции реальных средств измерения удаётся с достаточной степенью точности аппроксимировать простым выражением (n=2—3,n<m).

Если известен закон изменения величины x(t)_ист и передаточная функция средства измерения, то определяют изображение x(p)_изм= =W(p)x(p)_ист , а затем переходят к оригиналу.

Заменив p на jw, получим комплексную (амплитудно-фазовую) характеристику, действительная часть которой является амплитудно-частотной характеристикой A(w), а мнимая—фазо-частотной j(w).

27. Частотные характеристики средств измерений.

Амплитудно-частотная характеристика - это зависящее от частоты отношение амплитуды синусоидального выходного сигнала к амплитуде вызвавшего его синусоидального входного сигнала (то есть коэффициент усиления амплитуды).  ^ Фазо-частотная характеристика - это зависящий от частоты сдвиг фазы выходного синусоидального сигнала по отношению к фазе вызвавшего его синусоидального входного сигнала.  , . Комплексная частотная характеристика реального средства измерений представляет собой отношение двух полиномов от jw, причем степень полинома числителя не превосходит степени полинома знаменателя. На рис. 20 в качестве примеров представлены графики некоторых из перечисленных характеристик первого и второго порядка, чему соответствуют индексы у обозначений этих характеристик. Переходная характеристика и импульсная переходная характеристики второго порядка имеют колебательный характер, амплитудно-частотная характеристика может иметь максимум, а ее фазо-частотная характеристика с увеличением частоты стремится к (-/2). Фазо-частотные характеристики всех физически реализуемых динамических звеньев отрицательны. Это говорит о том, что преобразование изменяющихся во времени величин сопровождается запаздыванием, различным на различных частотах.  В ряде случаев достаточными для применения оказываются менее подробные частные динамические характеристики, такие как время реакции  средства измерений (см. рис. 20) и граничные значения частот, между которыми амплитудно-частотная характеристика отклоняется от своего номинального значения не более, чем на заданную величину. На рис. 20 показана лишь верхняя частота  частотной полосы.