
курсовая по метрологии отчет - 2012
.pdf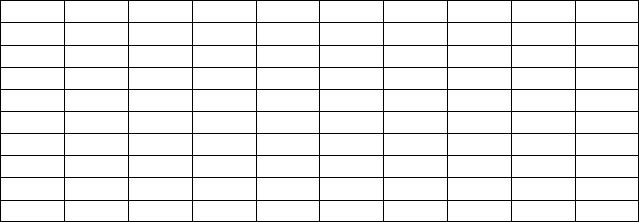
Задание к курсовой работе
Вариант 38
Путем взвешивания эталона определена ошибка ста весов. Результаты взвешивания сведены в таблицу:
-52 |
-142 |
34 |
-17 |
-88 |
-68 |
5 |
-232 |
9 |
65 |
-39 |
-76 |
68 |
3 |
34 |
-45 |
-106 |
-85 |
-115 |
-41 |
49 |
139 |
-141 |
-93 |
72 |
-14 |
-112 |
84 |
117 |
21 |
332 |
-92 |
69 |
-140 |
37 |
94 |
-42 |
-119 |
-205 |
-32 |
12 |
103 |
-84 |
-69 |
274 |
-39 |
-77 |
-131 |
177 |
-44 |
39 |
84 |
-41 |
-41 |
68 |
-70 |
-49 |
-71 |
-113 |
-183 |
56 |
16 |
64 |
-12 |
77 |
-113 |
-302 |
-85 |
51 |
-31 |
33 |
22 |
94 |
-94 |
83 |
76 |
4 |
121 |
0 |
-134 |
-54 |
177 |
59 |
59 |
-71 |
78 |
-78 |
-124 |
-29 |
-153 |
56 |
-107 |
-6 |
-6 |
-2 |
-129 |
24 |
117 |
-93 |
-159 |
Содержание работы:
1.Используя табличные значения необходимо найти математическое ожидание и дисперсию (Mx, Dx).
2.Найти доверительный интервал для Mx, Dx, соответствующий доверительной вероятности (1 – α) = 0,8.
3. Оценить вероятность попадания случайной величины X в интервал (0,6
÷ 1) X .
4.Для этой вероятности (3) найти интервал, соответствующий коэффициенту доверия (1 – α) = 0,85.
5.Построить гистограмму и эмпирическую функцию распределения.
6.Найти и построить доверительные области для f(x), соответствующие коэффициенту доверия (1 – α) = 0,9; и F(x), соответствующую коэффициенту доверия (1 – α) = 0,95.
7.Сгладить гистограмму и эмпирическую функцию распределения подходящим законом распределения.
8.Используя критерий согласия и критерий Колмогорова проверить правдоподобие гипотезы о совпадении выбранного закона распределения с истинным законом при уровне значимости α = 0,05.
1. Находим точечные оценки математического ожидания и дисперсии, учитывая, что n=100.
Выборочное среднее:
Исправленная дисперсия:
Выборочная дисперсия:
ˆ
MX
ˆ
DX
DX
x 1 |
n |
xi |
16,34 |
|||||
|
|
n |
i 1 |
|
|
|||
|
|
1 |
|
n |
(xi |
x)2 10295,68 |
||
n |
|
|
||||||
|
1 i 1 |
|
|
|
||||
|
1 |
n |
(xi |
x)2 10192,74 |
||||
|
n i 1 |
|
|
|
|
|
||
2. Рассчитываем доверительные интервалы для математического ожидания и дисперсии, доверительная вероятность (1 – α) = 0,8.
По формуле Ф( ) 1 0,40
2
и таблице значений Лапласа находим εα = 1,28.
Искомые доверительные интервалы будут иметь вид:
– для математического ожидания:
M1 ≤ MX ≤ M2,
|
|
|
ˆ |
|
|
М1,2 |
|
|
DX , |
|
|
X |
|
||||
|
|
|
n |
|
|
-29,42 ≤ MX ≤ -3,44. |
|||||
– для дисперсии: |
|
|
|
|
|
D1 ≤ DX ≤ D2, |
|
||||
|
|
|
ˆ |
|
|
D1,2 |
|
2(n 1)DX |
, |
||
( 2n 3) )2 |
|||||
|
|
||||
8690,57 ≤ DX ≤ 12528,92.
3. Находим точечную оценку вероятности попадания случайной величины Х в интервал (0,6 ÷ 1) Х = (-16,34; -9,80). Т.к. в этот интервал попало m=2 экспериментальных значения, то искомая оценка будет равна
ˆ |
m |
|
|
2 |
|
P(X ) |
n |
|
100 |
0,02 |
|
4. Рассчитываем доверительный интервал для вероятности P, оцененной в предыдущем пункте. Доверительная вероятность (1 – α) = 0,85. Тогда εα = 1,44 и искомый интервал имеет вид:
P1 ≤ P ≤ P2,

|
ˆ |
|
|
2 |
|
|
|
|
|
|
ˆ |
ˆ |
|
|
2 |
|
|
|
P |
2n |
|
|
|
|
|
|
|
|
|||||||
P1,2 |
|
|
|
|
|
|
P(1 P) |
|
|
, |
|||||||
|
|
|
|
|
|
2 |
|
|
n |
4n2 |
|||||||
1 |
|
|
2 |
|
1 |
|
|
|
|
|
|||||||
n |
|
|
|
|
n |
|
|
|
|
|
|
|
|
||||
0,0075 ≤ P ≤ 0,052.
5. Для построения гистограммы Г(x) заключаем все экспериментальные данные в интервал (-302; 332) и разбиваем его на 10 равных разрядов, каждый длиной Xi = Xi – Xi-1 = 63,4.
Частоты попадания экспериментальных точек в разряды гистограммы:
ˆ |
ni |
, i = 1, 2, …, r. |
||
Pi |
n |
|||
Значения гистограммы: |
|
|
|
|
|
Г(x) |
ni |
, |
|
|
|
|||
|
|
|
n X i |
|
где ni – число экспериментальных точек, попавших в разряд (Xi-1; Xi). По результатам расчетов составляем следующую таблицу:
Номер |
Разряд |
Число точек, |
Частота |
Значение |
|
разряда, |
попавших в |
попадания , |
гистограммы |
||
(Xi-1; Xi) |
|||||
r |
разряд, ni |
Pi |
Г(х) |
||
1 |
(-302; -238,6) |
1 |
0,01 |
0,00016 |
|
2 |
(-238,6; -175,2) |
3 |
0,03 |
0,00047 |
|
3 |
(-175,2; -111,8) |
14 |
0,14 |
0,00221 |
|
4 |
(-111,8; -48,4) |
21 |
0,21 |
0,00331 |
|
5 |
(-48,4; 15) |
23 |
0,23 |
0,00363 |
|
6 |
(15; 78,4) |
24 |
0,24 |
0,00379 |
|
7 |
(78,4; 141,8) |
10 |
0,10 |
0,00158 |
|
8 |
(141,8; 205,2) |
2 |
0,02 |
0,00032 |
|
9 |
(205,2; 268,6) |
1 |
0,01 |
0,00016 |
|
10 |
(268,6; 332) |
1 |
0,01 |
0,00016 |
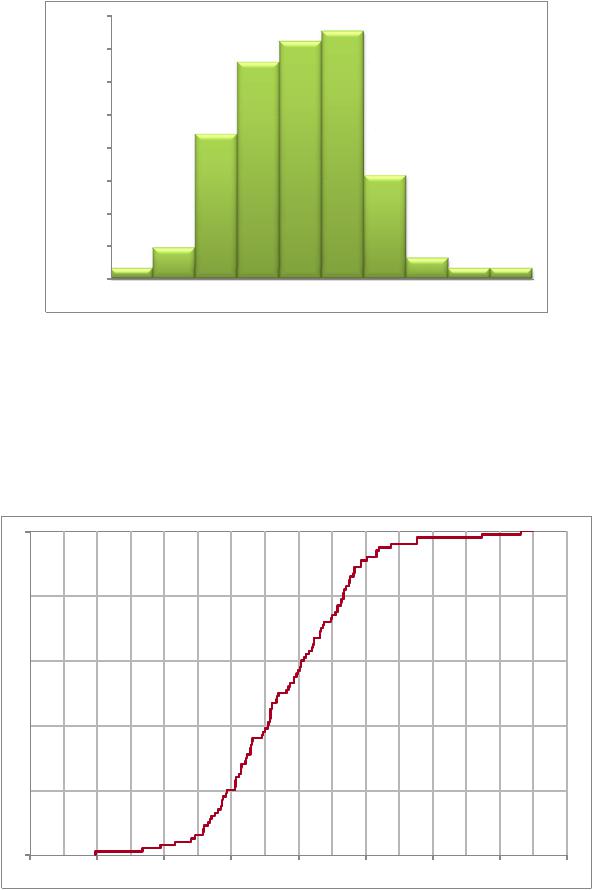
Рис.1. Гистограмма Г(х).
Соответствующую эмпирическую функцию рассчитываем по формуле
ˆ |
nx |
, |
F (x) |
n |
где nx – число экспериментальных точек, лежащих левее х.
Рис.2 Эмпирическая функция распределения случайной величины F(x).

6. Находим доверительные области для плотности распределения f(x) и функции распределения F(x).
В данном случае общее число разрядов равно 10 плюс два полубесконечных разряда: (–∞; –302) и (332; +∞). Таким образом, r = 12.
Выберем доверительную вероятность (1 – α) = 0,9.
Из условия Ф( ) 12 (1 r ) 0,4958 найдем εα' = 2,64.
Доверительную область (Pi1; Pi2) для вероятности Pi = P(Xi-1 < X < Xi) попадания исходной величины Х в этот разряд находим по формуле
|
|
ˆ |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ |
ˆ |
|
2 |
|||
|
|
Pi |
2n |
|
|
|
|
||||||
P |
|
|
|
|
|
|
Pi (1 |
Pi ) |
|
|
|||
|
|
|
|
|
|
|
|
|
|
||||
i1,i 2 |
|
|
2 |
|
2 |
|
n |
4n2 |
|||||
|
|
1 |
1 |
|
|||||||||
|
|
|
n |
n |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Затем для каждого разряда гистограммы находим доверительную область для плотности распределения:
|
|
f |
i1,i 2 |
|
Pi1,i 2 |
|
||
|
|
|
|
|
X i |
|
|
|
Результаты заносим в таблицу: |
|
|
|
|
|
|
||
|
|
|
|
|
Нижняя граница |
|
||
Номер |
Разряд |
Частота |
|
|
Верхняя граница |
|||
разряда, |
попадания, |
|
доверительного |
доверительного |
||||
(Xi-1, Xi) |
|
|||||||
r |
Pi |
|
|
|
интервала, fi1(x) |
интервала, fi2(x) |
||
|
|
|
|
|||||
1 |
(-∞; -302) |
0 |
|
|
|
0 |
0,00103 |
|
2 |
(-302; -238,6) |
0,01 |
|
|
|
0,00002 |
0,00130 |
|
3 |
(-238,6; -175,2) |
0,03 |
|
|
|
0,00012 |
0,00180 |
|
4 |
(-175,2; -111,8) |
0,14 |
|
|
|
0,00113 |
0,00402 |
|
5 |
(-111,8; -48,4) |
0,21 |
|
|
|
0,00194 |
0,00528 |
|
6 |
(-48,4; 15) |
0,23 |
|
|
|
0,00219 |
0,00562 |
|
7 |
(15; 78,4) |
0,24 |
|
|
|
0,00231 |
0,00579 |
|
8 |
(78,4; 141,8) |
0,10 |
|
|
|
0,00071 |
0,00326 |
|
9 |
(141,8; 205,2) |
0,02 |
|
|
|
0,00006 |
0,00156 |
|
10 |
(205,2; 268,6) |
0,01 |
|
|
|
0,00002 |
0,00130 |
|
11 |
(268,6; 332) |
0,01 |
|
|
|
0,00002 |
0,00130 |
|
12 |
(332; +∞) |
0 |
|
|
|
0 |
0,00103 |
|
0,01200
0,01000
0,00800
0,00600
0,00400
0,00200
0,00000
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
Рис.3. Гистограмма с доверительной областью.
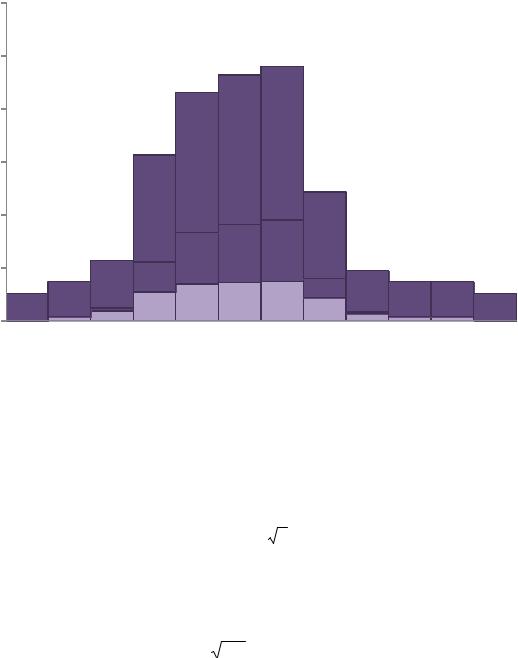
Находим доверительную область для функции распределения F(x).
F1(x) < F(x) < F2(x).
ˆ |
|
|
|
|
|
F1,2 F (x) |
n |
. |
|
|
Из условия K(λα) = 1 – α = 0,95 и таблицы предельного распределения Колмогорова находим λα = 1,36. Тогда
ˆ |
1,36 |
ˆ |
F1,2 F (x) |
100 |
F (x) 0,136 . |
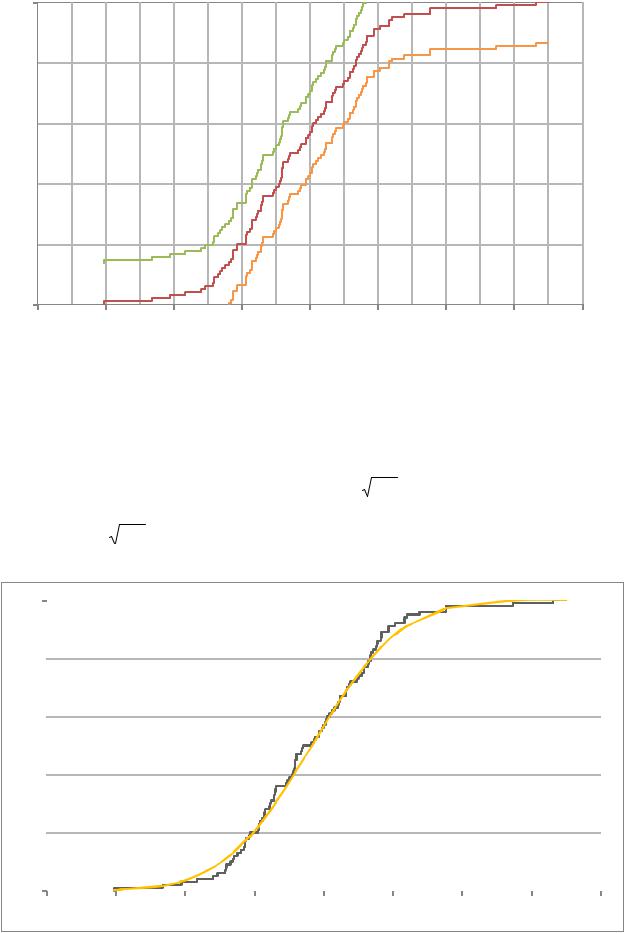
Учитывая, что функция распределения F(x) является вероятностью, и доверительная область для нее не может распространяться ниже нуля и выше единицы, делаем построение F1,2(x) на графике (рис.4).
1
0
400 |
300 |
200 |
100 |
0 |
100 |
200 |
300 |
400 |
Рис.4. Эмпирическая функция распределения с доверительными интервалами.
7. Из формы гистограммы следует, что гипотетическим распределением может быть нормальное распределение с функцией
|
|
|
|
|
1 |
|
x x |
) , |
|
|
|
|
|
|
|
FГ (x) 2 |
Ф( |
|
|
||
|
|
|
|
|
ˆ |
|||||
|
|
|
x x |
|
|
|
DX |
|
|
|
|
где |
Ф( |
) |
– функция Лапласа (определяется по таблице при |
||||||
|
||||||||||
|
|
|
ˆ |
|
|
|
|
|
||
|
|
|
DX |
ˆ |
– исправленная дисперсия. |
|||||
|
|
|
|
|
||||||
рассчитанных значениях аргумента), DX |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис.5. Эмпирическая и гипотетическая функции распределения.
Для плотности
|
1 |
|
( x x )2 |
|
|
ˆ |
|
f Г (x) |
|
e |
2DX . |
ˆ |
|||
|
2 DX |
|
|
0,00400
0,00000
0 |
2 |
4 |
6 |
8 |
10 |
12 |
14 |
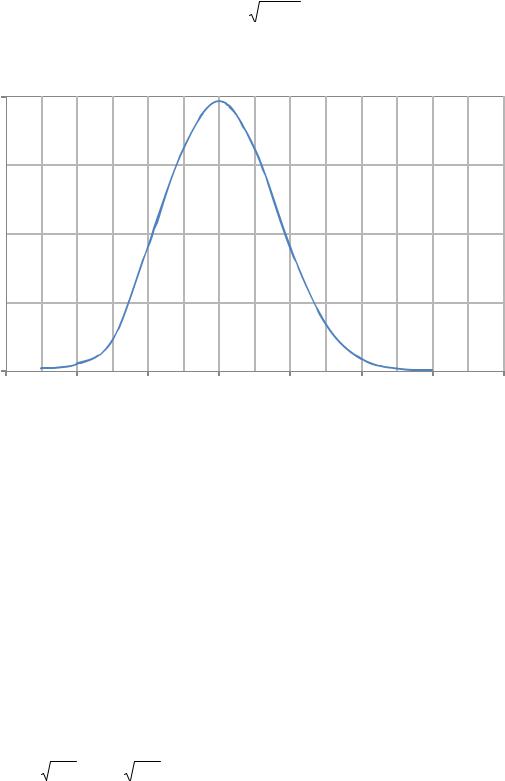
Рис. 6. Функция плотности распределения.
8.Для проверки гипотезы H0: F(x) = Fг(х) при уровне значимости
α= 0,05 используем вначале критерий согласия χ2.
Экспериментальное значение критерия хи-квадрат
|
r |
ˆ |
2 |
|
э2 |
n |
(Pi Pi ) |
|
, |
Pi |
|
|||
|
i 1 |
|
|
где ˆ
Pi i-й разряд,
Pi Ф(
– экспериментальная частота попадания случайной величины Х в
хi x |
) Ф( |
xi 1 x |
) – гипотетическая вероятность попадания |
ˆ |
|
||
|
ˆ |
||
DX |
|
DX |
|
случайной величины в i-й разряд. Результаты расчетов заносим в таблицу:

Номер |
Экспериментальная |
Гипотетическая |
|
ˆ |
2 |
|
|
разряда, |
|
(Pi Pi ) |
|
|
|||
частота попадания, |
ˆ |
частота попадания, Pi |
|
|
|
|
|
|
Pi |
|
|
||||
r |
Pi |
|
|
|
|||
|
|
|
|
|
|
|
|
1 |
0,01 |
|
0,00312 |
|
0,015 |
|
|
2 |
0,03 |
|
0,01469 |
|
0,016 |
|
|
3 |
0,14 |
|
0,08774 |
|
0,031 |
|
|
4 |
0,21 |
|
0,15870 |
|
0,017 |
|
|
5 |
0,23 |
|
0,23570 |
|
0,000 |
|
|
6 |
0,24 |
|
0,23240 |
|
0,000 |
|
|
7 |
0,1 |
|
0,16200 |
|
0,024 |
|
|
8 |
0,02 |
|
0,07490 |
|
0,040 |
|
|
9 |
0,01 |
|
0,02449 |
|
0,009 |
|
|
10 |
0,01 |
|
0,00616 |
|
0,002 |
|
|
|
r |
ˆ |
|
2 |
r |
ˆ |
2 |
|
Таким образом, э2 |
n |
(Pi Pi ) |
|
100 |
(Pi Pi ) |
|
13,899 |
|
|
|
Pi |
|
|||||
|
i 1 |
|
Pi |
|
i 1 |
|
|
|
Гипотетическое значение критерия хи-квадрат при выбранном уровне
значимости α = 0,05 и числе степеней свободы s = r – 1 – k = 12 – 1 – 2 = 9
χα2 = 16,919.
Так как χэ2 < χα2, выбранная гипотеза является правдоподобной по критерию хи-квадрат.
Проверим ту же самую гипотезу с помощью критерия согласия Колмогорова. Максимальное различие между гипотетической и эмпирической функциями распределения:
ˆ . D max | FГ (x) F (x) | 0,045
Экспериментальное значение критерия Колмогорова:
э D n 0,045
n 0,045 100 0,45 .
100 0,45 .
Гипотетическое значение того же самого критерия при уровне значимости α = 0,05 равно λα = 0,52.
Так как λэ < λα, то гипотеза H0 является правдоподобной также и по критерию Колмогорова.
