ответы на экзамен / 12 Интеграл Лапласа

Интеграл Лапласа.

Подставим в интеграл (5) функцию нормального распределения , тогда: 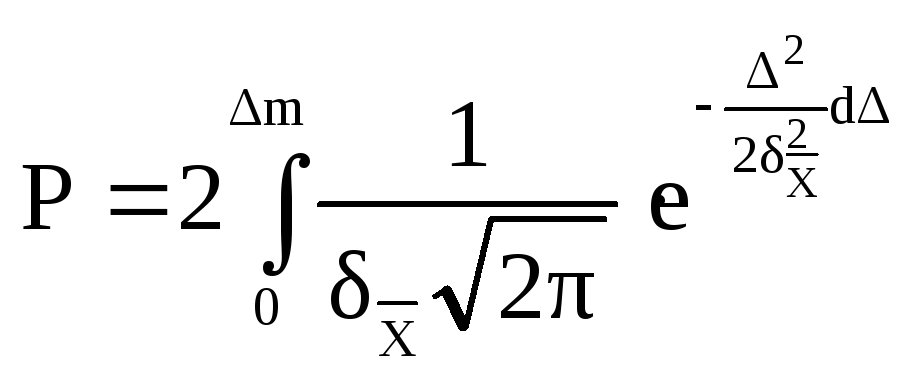. Пусть (6), при n=const, , z – безразмерная величина.

Тогда max значение , т.е. границей доверительного интеграла будет max значение параметра z. (7), тогда: 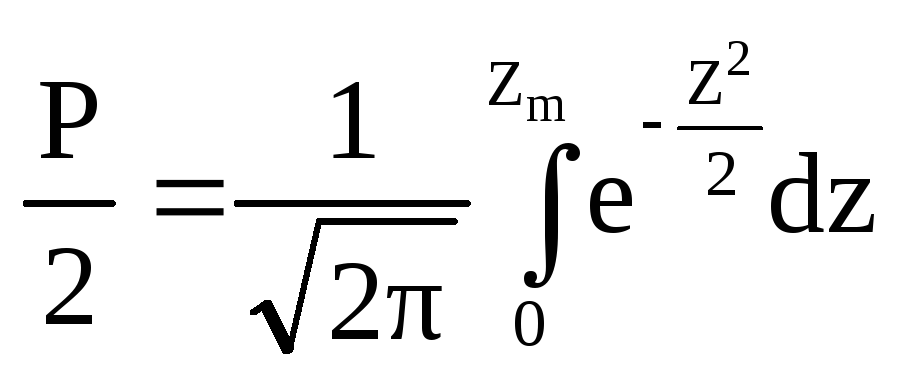(8) интеграл Лапласа.

Значение интеграла Лапласа определяет половину доверительной вероятности и соответствующее ей значение доверительного интеграла. Значение этого интеграла зависит от верхнего предела (от)., он не вычисляется в элементарных функциях.

При ,

Вывод: max возможное значение погрешности случайного характера, т.е. подчиняющегося теории ошибок не должно превышать значение - это цена max значения погрешности случайного характера случайной величины . Для оценки абсолютной погрешности Х принято равенство (9). (9) – критерий выявления промахов. При обнаружении промахов, значения исключаются и нормированные характеристики () должны быть рассчитаны заново.