ответы на экзамен / 5 Прямое равноточное измерение и его нормированные метрологиче

Прямое равноточное измерение и его нормированные метрологические характеристики.

При этом считаем, что значение Х неизвестно.

Для определения действительного значения измеряемой величины , которое является оценкой истинного её значения проводится серия измерений одним и тем же измерительным прибором и строится таблица измеренных значений.

1. Для оценки 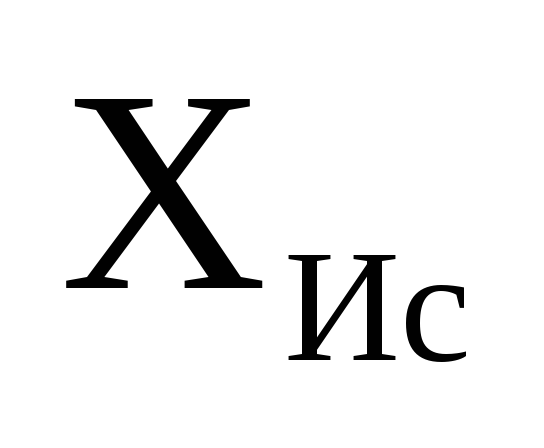вводится первая метрологическая нормированная характеристика – среднее арифметическое значение 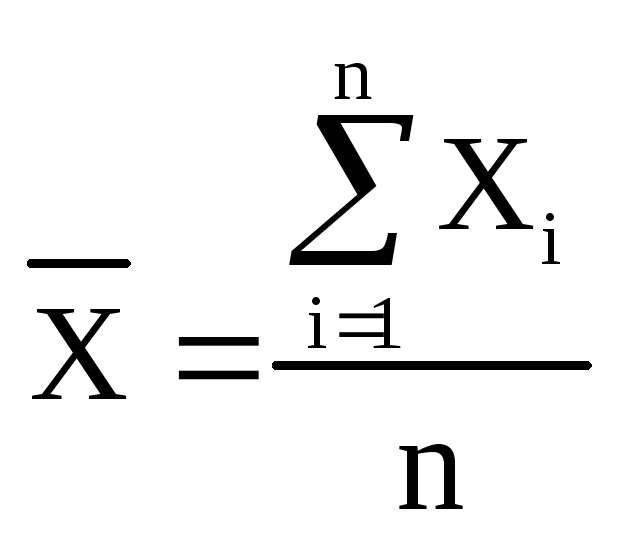. Для данной серии измерений найденное 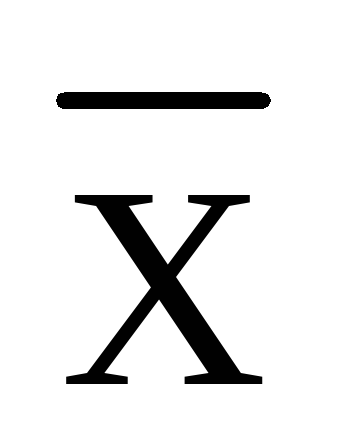и будет действующим значением 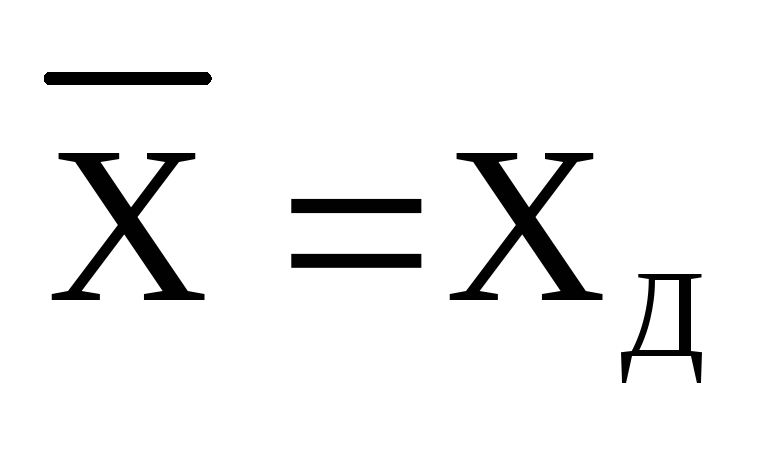. При этом выполняется следующее правило, установленное опытным путём: чем больше проведено измерений, тем ближе действительное значение приближается к истинному.

2. Второй метрологической характеристикой является

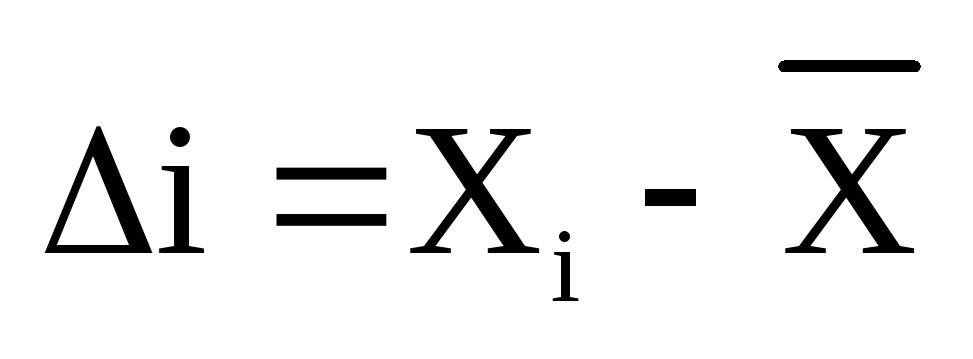
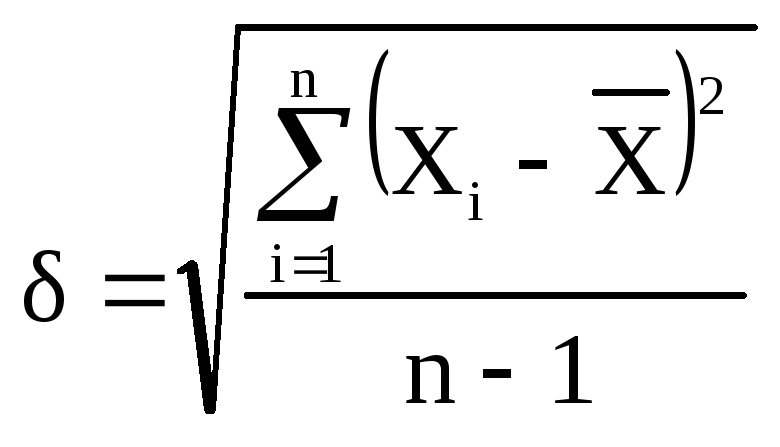3. Третьей метрологической нормированной характеристикой является - средняя лв. погрешность по серии измерений . Для данной серии измерений является некоторой постоянной величиной. Иногда кроме учитывается дисперсия 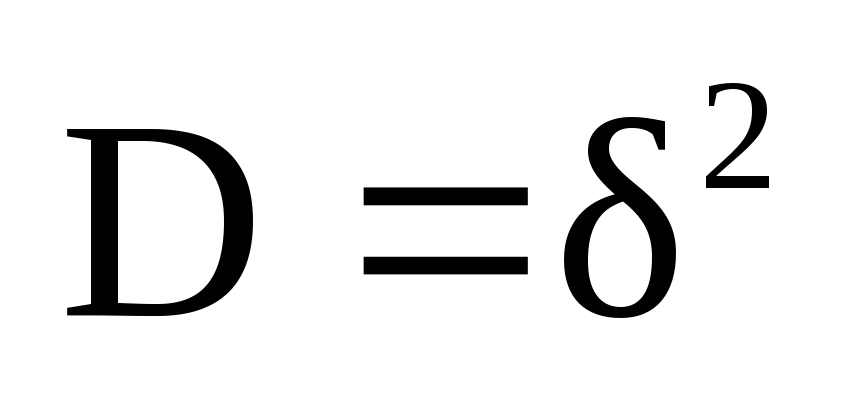. Дисперсия определяет степень разброса измерений (измеряемых величин) относительно среднего арифметического. Величина дает оценку погрешности случайного характера, измеряемой величины Х по всей серии измерений. Сами однократно измеренные значения 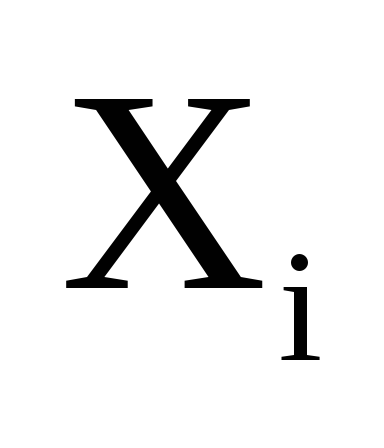в силу разнообразных случайных причин не намного отличаются друг от друга, поэтому сама измеряемая величина ведёт себя случайным образом и называется случайной величиной.

4. При проведении другой серии измерений с большей или меньшей n будет меняться действующее значение искомой величины, т.е. её среднее арифметическое , поэтому 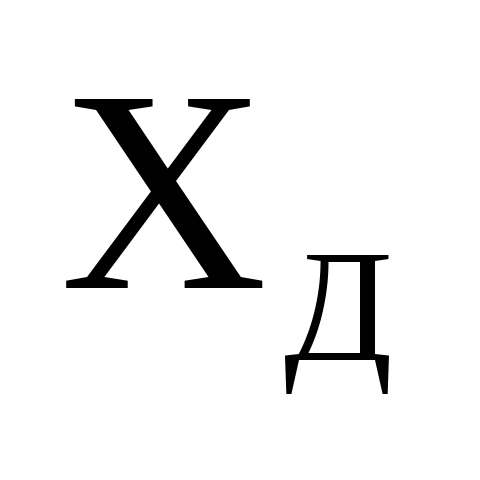так же является величиной случайной и для оценки её погрешности вводится 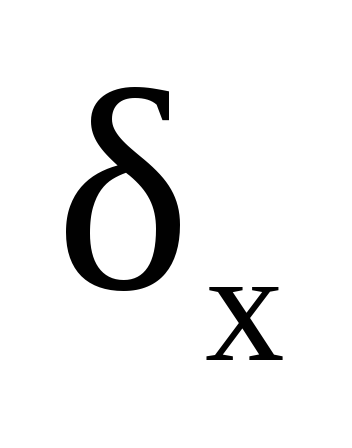- среднее арифметическое от средней квадратической погрешности и определяется по формуле: .

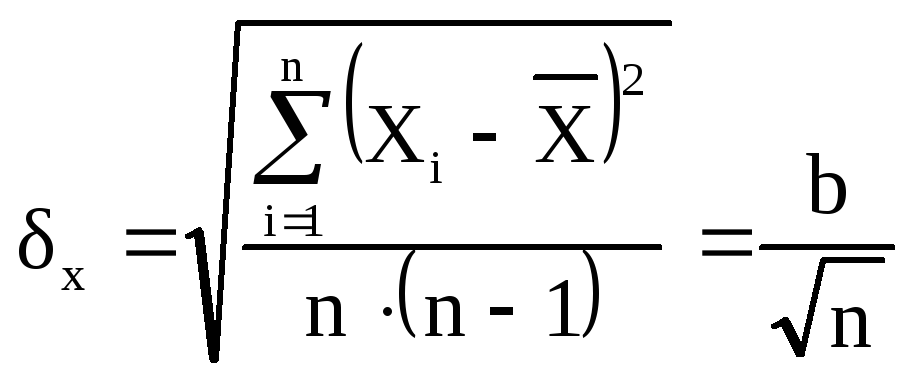5. Математическое ожидание измеряет величина M, которая представляет собой некоторый заранее оговорённый интервал, в который входят измеряемые величины с тем или иным значением вероятности, которая называется доверительной вероятностью P. 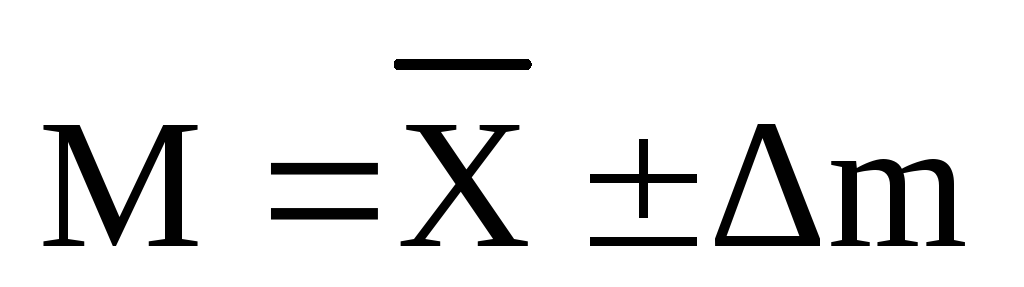, где - максимально допустимая абсолютная погрешность измерения, которая называется границей доверительного интервала или просто доверительным интервалом, при этом доверительный интервал однозначно связан с доверительной вероятностью P определенной интегральным соотношением.

Вывод: таким образом математическое ожидание измеренной величины Х по данной проведённой серии измерений даёт оценку истинного значения измеряемой величины, а так же максимальную допущенную погрешность измерений, т.е. ;

Нахождение H является целью прямого равноточного измерения.