
ответы на экзамен / 7 Примеры функций распределения случайной величины
.docПримеры функций распределения случайной величины.
В зависимости от вида гистограммы можно ввести следующие законы распределения случайной величины.
-
Равномерный закон распределения случайной величины.
-
Треугольный закон распределения случайной величины.
-
Трапецеидальный закон распределения случайной величины.
-
Нормальный закон распределения случайной величины, график имеет следующий вид.
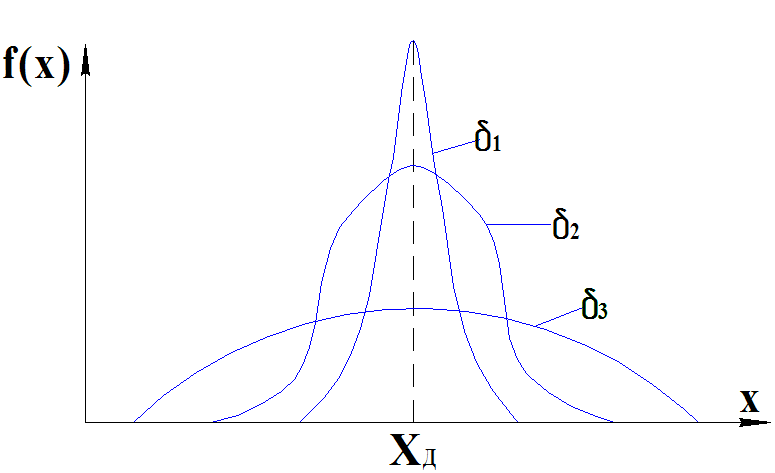
Каждая из кривых симметрична и отличается
своей остротой
![]() >
>![]() >
>![]()
Немецкий математик Гаус нашёл аналитический
вид нормального закона распределения
случайной величины, проявляющегося при
большом числе измерений или в серии
большой выборки. Вид нормального закона
распределения:
![]() .
.
Свойства нормального закона распределения случайной величины:
-
Параметром функции распределения является
 ,
т.е. среднее квадратичное значение.
,
т.е. среднее квадратичное значение. -
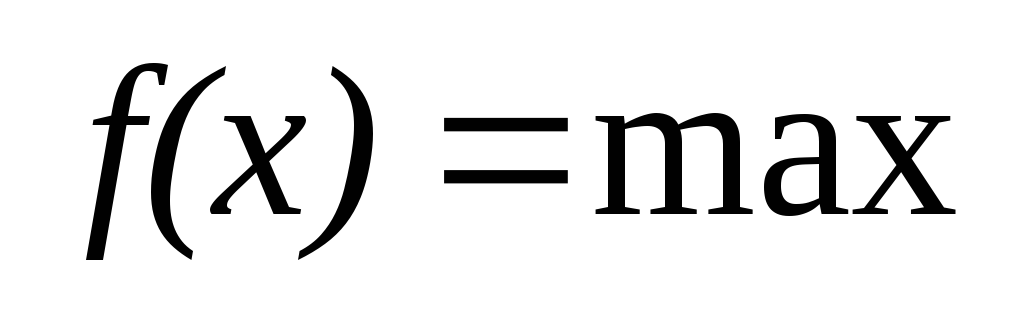 в центре распределения, при всех других
х правее или левее центра распределения
вероятность такого значения х убывает.
в центре распределения, при всех других
х правее или левее центра распределения
вероятность такого значения х убывает. -
Функция Гаусса симметрична относительно центра распределения, т.е. при измерениях появления как меньших так и больших значениях х относительно
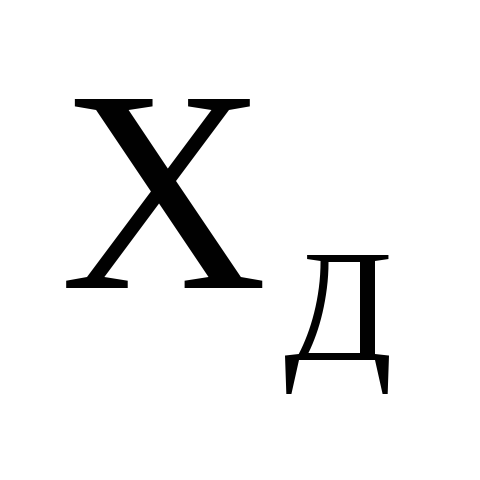 равномерно.
равномерно.
Они показывают, что при серии измерений малой выборки закон распределения измеренной величины все более отклоняется т.е. видоизменяется относительно нормального закона.
