Приложение а

Правила округления погрешности и результата измерения

В нормативном документе МИ 1317-86 установлено, что при округлении числовых значений погрешностей измерений должно оставаться не более двух значащих цифр. А именно,

– если первая значащая цифра числа, выражающего погрешность, равна 1 или 2, то значение погрешности округляется до двух значащих цифр. При этом округление проводится всегда в большую сторону;

– если первая значащая цифра числа, выражающего погрешность, равна 3 и более, то значение погрешности округляется до одной значащей цифры. При этом округление проводится по правилам математики.

При записи результатов измерений количество наименьших разрядов числовых значений результата измерения должно соответствовать количеству наименьших разрядов числовых значений погрешностей.

Правила округления числовых значений

Практикой выработаны следующие правила округления числовых значений при оформлении результатов и погрешностей измерений.

1. Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются. Если десятичная дробь в числовом значении результата измерения оканчивается нулями, то нули отбрасываются только до того разряда, который соответствует разряду погрешности, например, результат 2,0700, погрешность 0,001; результат округляют до 2,070.

2. Если цифра старшего из отбрасываемых разрядов меньше 5, то остающиеся цифры числа не изменяют, например, число 253435 при сохранении четырех значащих цифр Должно быть округлено до 235400, число 235,435—до 235,4.

3. Если цифра старшего из отбрасываемых разрядов больше или равна 5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу, например, при сохранении трех значащих цифр число 18598 округляют до 18600, число 152,56 — до 153.

4. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или нули, то последнюю сохраняемую цифру не изменяют, если она четная и увеличивают, если она нечетная, например, число 22,5 при сохранении двух значащих цифр округляют до 22, а число 23,5 — до 24.

Приложение б Пример поясняющих рисунков

Поясняющие рисунки приводятся для результатов измерений одного и того размера объема, полученных с помощью двух разных средств измерений. Площади, ограниченные ординатами и абсциссами, отражающие плотность распределения погрешности вокруг полученного значения объема выбранного цилиндра должны быть одинаковыми. Методика построения поясняющих рисунков приведена в приложении В (раздел В.9).

Вместо буквенных обозначений в отчете привести соответствующие числовые значения указанных величин.

V_мк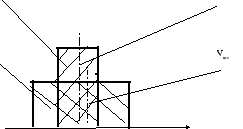

%

%

-V_шт -V_мк +V_мк +V_шт

Приложение в

Методические указания к выполнению лабораторной работы

Методический материал приведен в порядке следования пунктов выполнения лабораторной работы

В.1 Измерения с помощью средств измерения

В.1.1 Измерения с помощью штангенциркуля

Штангенприборы – к ним относят средства линейных измерений, объединенные общим принципом построения отсчетных устройств, основанным на применении линейного нониуса. В зависимости от назначения различают штангенциркули, штангенглубиномеры, штангенрейсмассы. Штангенциркуль — универсальное средство измерения длины, диаметров валов и отверстий, глубины отверстий и расстояний между центрами отверстий.

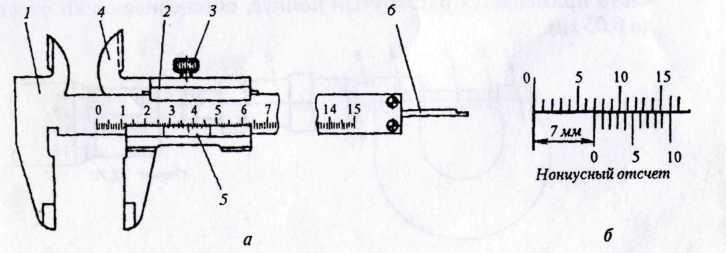
Рисунок В.1 – Штангенциркуль

Штангенглубиномер предназначен для измерения глубины отверстий, пазов и т.п.

Штангенрейсмасс – средство измерения высотных размеров изделий.

Принцип построения нониуса заключается в совмещении соответствующих штрихов двух линейных шкал, интервалы деления которых отличаются на определенную величину. В общем случае штангенприбор, приведенный на рисунке В.1 состоит из штанги 1 с неподвижной измерительной губкой и рамки 2, перемещающейся по штанге, с другой измерительной губкой. На штанге нанесена шкала с ценой деления 1 мм. На скосе рамки нанесена вспомогательная шкала 5, называемая нониусом, с ценой деления 0,9 мм, по которой отсчитываются дробные доли миллиметра. Для фиксирования рамки на рабочей части штанги служит винт 3. Рамка жестко связана с линейкой глубиномера 6. Верхние губки 4 предназначены для измерения внутренних размеров, а нижние – наружных.

При совмещении нулевой отметки шкалы нониуса с нулевой отметкой шкалы штанги, первая за нулевой отметка шкалы нониуса оказывается смещенной относительно первой отметки шкалы штанги на 0,1 мм; соответственно вторая отметка шкалы нониуса будет смещена на 0,2 мм, а десятая на 1 мм, т.е. последняя отметка шкалы нониуса точно совпадает с отметкой 0,9 мм на шкале штанги.

Если при измерении размера шкала нониуса располагается так, что одна из отметок нониуса (не нулевая) совпадает с какой-либо отметкой шкалы штанги (не нулевой), то результат измерения определяется как сумма отсчетов по шкале штанги и произведения разности цены деления шкал штанги и нониуса на номер деления шкалы штанги, с которым совпала отметка нониуса. Так, измеренное значение на рисунке 1 будет равно = 7 + 0,1 =7,1 мм. Таким образом, с помощью нониуса можно произвести отсчет размера с точностью до 0,1 мм. В штангенприборах часто применяется растянутый нониус, обеспечивающий отсчет размера до 0,05 мм. В некоторых современных моделях штангенприборов вместо нониуса применяются индикаторы часового типа с ценой деления 0,01 мм.

В.1.2 Измерения с помощью микрометра

Микрометрические приборы (микрометры, микрометрические глубиномеры, микрометрические нутромеры) являются более точными, чем штангенприборы. Принцип действия микрометрических приборов основан на преобразовании вращательного движения точного микрометрического винта, установленного в неподвижную гайку, в его поступательное движение вдоль оси. Большинство микрометрических приборов имеет винт с шагом 0,5 мм, поэтому поворот винта в гайке на 360° приводит к его перемещению вдоль оси на 0,5 мм.

Микрометр, приведенный на рисунке В.2 состоит из скобы 7, с одной стороны которой запрессована неподвижная пятка 2, а с другой укреплена микрометрическая головка, состоящая из стебля 5, барабана 6 в сборе с микровинтом 3 и механизмом трещотки 7. При вращении барабана стебель совершает поступательное движение и приводится в контакт с измеряемым объектом. Механизм трещотки обеспечивает при этом постоянство измерительного усилия. Винт 4 фиксирует положение микровинта. Перемещение микровинта отсчитывается по двум шкалам: одной, нанесенной по длине стебля, и второй, нанесенной по окружности барабана. Деления на стебле нанесены через 0,5 мм, а на шкале барабана имеется 50 отметок. Таким образом, одно деление шкалы барабана соответствует перемещению микровинта на 0,5/50 - 0,01 мм.

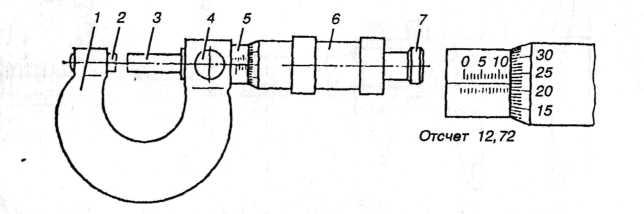
Рисунок В.2 - Микрометр

Для микрометрических приборов установлены два класса точности (1 и 2). Предельно допускаемая погрешность микрометрических приборов зависит от диапазона измерения. Так, для микрометров с пределами измерения от 0 до 25 мм, класса точности 1, погрешность прибора не превышает ±0,002 мм, а у микрометров для измерения длин в диапазоне от 400 до 500 мм, не превосходит ±0,005 мм.

В.2 Погрешность прямых измерений

Погрешность прямых однократных измерений определяется систематической составляющей, так как случайная составляющая погрешности в этом случае существенно мала по сравнению с систематической и ею можно пренебречь.

Если систематические составляющие погрешности результатов прямых измерений не известны заранее, то они оцениваются каждая по отдельности, исходя из формулы, приведенной в Р 50.2.038 (п.6.2.1) как неисключенные систематические погрешности:

,

где Θ_i - граница i-й неисключенной систематической погрешности;

k - коэффициент, определяемый принятой доверительной вероятностью и числом m составляющих Θ_{i ;}

m - число составляющих неисключенной систематической погрешности.

В.3 Субъективная составляющая систематической погрешности

Субъективная (личная) погрешность измерения обусловлена погрешностью отсчета оператором показаний по шкалам СИ, диаграммам регистрирующих приборов. Они вызываются состоянием оператора, его положением во время работы, несовершенством органов чувств, эргономическими свойствами СИ. Характеристики личной погрешности определяют на основе нормированной номинальной цены деления шкалы измерительного прибора (или диаграммной бумаги регистрирующего прибора) с учетом способности "среднего оператора" к интерполяции в пределах деления шкалы.

Пример. Пусть цена деления равномерной шкалы равна Х_д единиц измеряемой физической величины, длина деления равна L_д мм. Определить наибольшее значение личной погрешности.

При условии, что средний оператор может интерполировать в пределах деления шагами по 0,2 деления, т.е. по 0,2L_д, наибольшее значение личной погрешности

∆x _опер = x_{д ·} 0,2L_д/ L_д = 0,2 x_д.

Погрешность является априорной. Ее можно заранее предусмотреть, рассчитать, исключить путем введения в виде поправки в получаемые результаты измерений.

С = - ∆x _опер,

где С – поправка в мм.

При проведении однократных измерений должна быть уверенность в том, что погрешности метода и оператора малы по сравнению с допускаемой погрешностью измерений (обычно допускается их сумма не свыше 30 % от допускаемой погрешности измерений). Поэтому перед проведением измерений принимают меры по определению влияющих факторов и принимаются всевозможные меры, направленные на уменьшение их влияния (термостатирование, экранирование и т.д.), вводятся значения поправок, выбирается средство измерений, изучаются его метрологические характеристики.

В.4 Погрешность влияния внешних условий

Погрешность влияния внешних условий возникает вследствие изменения линейных размеров измеряемой величины под действием изменения температуры окружающей среды и зависит от температурного коэффициента линейного расширения тела.

Температурный коэффициент линейного расширения – физическая величина, равная относительному изменению линейного размера величины X при изменении температуры окружающей среды на один градус.

где ∆x_вн – изменение величины x, вызванное изменением температуры на ∆Т градусов ^оС ;

∆Т- отклонение температуры окружающей среды Т от 20 ^оС ;

x_o - значение величины при 20 ^оС.

В диапазоне температур от 20 до 200 ^оС можно считать, что расширение стали описывается линейным законом:

где x – измеренное значение величины при температуре Т;

x_o – значение величины при 20 ^оС;

λ_х - температурный коэффициент линейного расширения величины x.

Температурный коэффициент линейного расширения стали:

λ _стали = 11 10 ^{-6 о}С ^-1 .

В.5 Оценивание методической погрешности

При обработке результатов измерения физических величин, особенно когда производятся косвенные измерения, нередко используются табличные данные или иррациональные константы, такие, как плотности веществ, ускорение свободного падения, диэлектрическая и магнитная проницаемость, длины световых волн, результаты предыдущих приближенных вычислений, значения тригонометрических функций и так далее. В этом случае следует учитывать тот факт, что и те, и другие, как правило, представляют собой числа, округленные до некоторого знака. В силу этого они являются приближенными числами и вносят свою долю в погрешность результата измерения, снижая его точность. Эту долю необходимо оценивать и в зависимости от задачи принимать во внимание или нет. С другой стороны некорректная запись результата измерения или его погрешности может приводить к тому, что создается ложное впечатление о высокой точности измерения.

Рассмотрим погрешность иррациональных констант на примере.

Пример. Пусть необходимо определить длину внешней окружности вала путем измерения диаметра вала с последующим вычислением длины окружности по формуле

L = π · D

Допустимая относительная погрешность измерения должна быть не более, чем 0,2 %. Требуется выбрать средство и метод измерения, обеспечивающие заданную точность.

Для определения длины окружности вала предложено использовать рычажную скобу с отсчетным устройством типа СР, паспортная погрешность которой равна ± 0,002 мм. Измеренный диаметр вала равен D = 1,278 мм.

При вычислениях длины окружности использовалось значение π = 3,14, которое, как известно, является числом иррациональным. В предположении, что последующие знаки в числе π неизвестны, и что значение 3,14 получено в результате округления, по правилам округления погрешность его следует оценить величиной 0,005. Тогда погрешность измерения длины окружности будет равна

Эта величина значительно превышает допустимую, равную 0,2 %. При этом видим, что погрешность, вносимая числом л по величине такая же, как и погрешность, вносимая рычажной скобой .

Чтобы уменьшить погрешность измерения длины окружности, нужно уменьшать ее составляющие погрешности. Уменьшить погрешность измерения диаметра весьма проблематично, так как для этого потребовалось бы использовать сложное дорогостоящее оборудование, например, универсальный измерительный микроскоп УИМ-23, измерения на котором весьма трудоемки и требуют высокой квалификации оператора.

Но это затруднение весьма просто обходится, если принять во внимание, что на самом деле с большей степенью приближения значение л можно записать как л = 3,1416.В этом случае при использовании в вычислениях значения π = 3,14 его погрешность следует принять равной не 0,005, как это было сделано выше, а только лишь 0,0016. Тогда погрешность измерения длины окружности будет:

,

что соответствует требованиям поставленной задачи.

Если при измерениях используются табличные данные, то в этом случае оценка вносимой погрешности производится аналогично вышеизложенному.

В.6 Погрешность косвенных измерений

Оценивание систематической погрешности косвенных измерений проводится в соответствии с МИ 2083-90 «Рекомендация. ГСИ. Измерения косвенные. Определение результатов измерений и оценивание их погрешностей», а также на основе практического справочного руководства «Расчет оценок погрешностей измерения» Н.Н.Казанцевой.

Согласно МИ 2083, если искомое значение А связано с m измеряемыми аргументами a_1., a₂, … , a_m , уравнением

где b_1., b₂, … , b_m , – постоянные коэффициенты при аргументах a_1., a₂, … , a_m соответственно,

и неисключенные систематические погрешности результатов измерений аргументов заданы границами Θ_ai , то доверительные границы неисключенной систематической погрешности результата косвенного измерения Θ_p (без учета знака) при вероятности Р вычисляют по формуле:

,

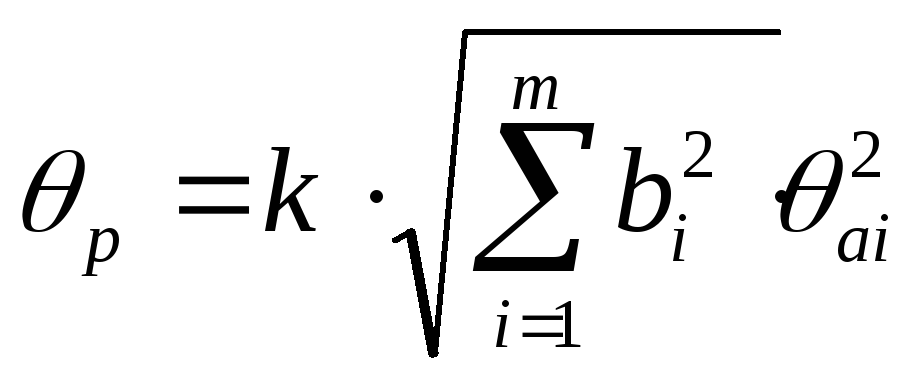где k - поправочный коэффициент, определяемый принятой доверительной вероятностью и числом m составляющих Θ_ai (при доверительной вероятности Р = 0,95 поправочный коэффициент принимают равным 1,1);

b _i - постоянные коэффициенты при аргументах a_i.;

Θ_ai- неисключенная систематическая погрешность результата измерений i-го аргумента.

При этом, если систематические составляющие погрешности результатов прямых измерений аргументов Θ_ai не известны заранее, то они оцениваются каждая по отдельности, исходя из формулы, приведенной в Р 50.2.038 (п.6.2.1):

,

где Θ_i - граница i-й неисключенной систематической погрешности аргумента;

k - коэффициент, определяемый принятой доверительной вероятностью и числом m составляющих Θ_{i ;}

m - число составляющих неисключенной систематической погрешности аргумента.

Рассмотрим подробнее. При косвенных измерениях результат у определяется по известной функциональной зависимости у от величин аргументов х₁, х₂, ... х_n определяемых обычно прямыми измерениями:

y=f(x_1, x₂ … x_n). (В.1)

Пусть при измерении величин х₁, х₂,... х_n присутствуют только систематические погрешности ∆х₁, ∆х₂,...∆х_n.

Запишем полный дифференциал функции

.

Абсолютные погрешности измерения аргументов есть не что иное, как их малые приращения ∆х₁, ∆х₂,...∆х_n обусловливающие малое приращение функции ∆у т.е. абсолютную погрешность косвенного измерения, которую можно записать в виде:

(В.2)

Знаки погрешностей измерения аргументов заранее, как правило, неизвестны, поэтому получаемые при дифференцировании отрицательные знаки производных целесообразно не учитывать и суммирование производить по модулю. При этом полученное значение погрешности измерения является оценкой сверху.

С учетом случайного характера знаков ∆х₁, ∆х₂,...∆х_n и в отсутствии корреляции между аргументами х₁, х₂, ... х_n при определении погрешности ∆у вместо формулы (В.2) используется формула геометрического (квадратичного) суммирования ¹⁾ :

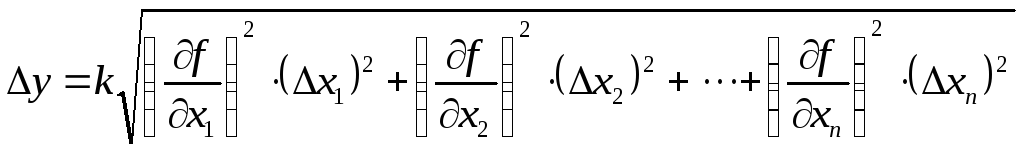(В.3)

Примечание – При вычислении суммарной погрешности по выражению (В.3) обращайте внимание на размерности входящих в это выражение величин для того, чтобы размерность суммарной погрешности совпадала с размерностью результата косвенных измерений Y (В.1).

Вычисления по формулам (В.2) и (В.3) могут представлять определенные затруднения, но они существенно упрощаются, если функция выражается в виде произведения сомножителей

, (В.4)

где с, α, β, γ любые положительные или отрицательные константы.

В этом случае вычисление абсолютной погрешности ∆y можно заменить вычислением относительной погрешности

Логарифмирование и последующее дифференцирование (В.4) с заменой dx и dy на ∆x и ∆y дает

,

.

П

рименив геометрическое суммирование, получим

откуда легко определяется абсолютная погрешность

.

^{__________________}

¹⁾ Выбор той или иной формулы для оценки зависит от числа аргументов в исходной формуле

Е

сли слагаемых под корнем не более трех, то, целесообразно применить суммирование модулей погрешностей.

В тех случаях, когда нужно определить возможную предельную погрешность результата измерения при n > 3, применяют простое суммирование модулей слагаемых в формуле (В.2).

Окончательный результат косвенных измерений представляется в виде:

y _д = y ± Δ y, при Р = 0,95

где y и Δy – значения, полученные в соответствии с правилами округления погрешностей и результата измерений.

В.7 Правила округления погрешности и результата измерения

Распространенной ошибкой при оценивании результатов и погрешностей измерений является вычисление их и запись с чрезмерно большим числом значащих цифр. Этому способствует использование для расчетов средств вычислительной техники, позволяющих практически без лишних затрат труда и времени получать результаты расчета с четырьмя и более значащими цифрами. Необходимо помнить, что поскольку погрешности измерений определяют лишь зону недостоверности, неопределенность результатов, т.е. дают представление о том, какие цифры в числовом значении результата являются сомнительными, их (погрешности) не требуется знать очень точно.

В самом деле, вычислив значение погрешности равным 0,43293 и результата измерения 19,82256, следует задуматься, имеет ли смысл запись результата с такой погрешностью. Ведь если исходить из того, что недостоверность результата уже характеризуется десятыми долями (0,4...), то очевидно, что вклад последующих значащих цифр в оцененную погрешность будет все менее и менее весом и ничего не прибавит к информации об измеряемой величине. С учетом этого необходимо ограничивать и число значащих цифр в записи результата измерения.

Документом МИ 1317 установлено, что при округлении числовых значений погрешностей измерений должно оставаться не более двух значащих цифр. А именно,

Правило 1

– если первая значащая цифра числа, выражающего погрешность, равна 1 или 2, то значение погрешности округляется до двух значащих цифр. При этом округление проводится всегда в большую сторону;

– если первая значащая цифра числа, выражающего погрешность, равна 3 и более, то значение погрешности округляется до одной значащей цифры. При этом округление проводится по правилам математики.

Значащие цифры данного числа – это все цифры от первой слева, не равной нулю, до последней записанной цифры справа. При этом нули следующие из множителя 10 ⁿ, не учитываются.

Число	Кол-во значащих цифр
12,0	три
30	две
120. 10 3	три
0,514	три
0,0056	две

Правило 2

При записи результатов измерений количество наименьших разрядов числовых значений результата измерения должно соответствовать количеству наименьших разрядов числовых значений погрешностей. В приведенном примере, следовательно, оценка погрешности должна быть записана как 0,43 или 0,4, а результат измерения как 19,82 или 19,8 соответственно.

В.8 Правила округления числовых значений

Практикой выработаны следующие правила округления числовых значений при оформлении результатов и погрешностей измерений.

1) Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются. Если десятичная дробь в числовом значении результата измерения оканчивается нулями, то нули отбрасываются только до того разряда, который соответствует разряду погрешности, например, результат 2,0700, погрешность 0,001; результат округляют до 2,070.

2) Если цифра старшего из отбрасываемых разрядов меньше 5, то остающиеся цифры числа не изменяют, например, число 253435 при сохранении четырех значащих цифр должно быть округлено до235400, число 235,435—до 235,4.

3) Если цифра старшего из отбрасываемых разрядов больше или равна 5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу, например, при сохранении трех значащих цифр число 18598 округляют до 18600, число 152, 56 — до 153.

4) Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или нули, то последнюю сохраняемую цифру не изменяют, если она четная и увеличивают, если она нечетная, например, число 22,5 при сохранении двух значащих цифр округляют до 22, а число 23,5 — до 24.

Следует различать записи приближенных чисел по количеству значащих цифр.

Примеры:

1. Следует различать цифры 2,4 и 2,40

– запись 2,4 означает, что верны только цифры целых и десятых; истинное значение числа может быть , например,2,43 или 2,38

– запись 2,40 означает, что верны и сотые доли; истинное значение числа может быть2,401, 2,403 или 2, 404

2 Числовое значение величины и ее погрешности записывают с указанием одной и той же единицы физической величины (80,555 + 0,002) кг.

3 Интервалы между числовыми значениями величин записывают:

-… от 60 до 100…;

-… свыше 100 до 120… .

4. Округление следует выполнять сразу до желаемого количества значащих цифр, а не по этапам.

Например округление числа 565,46 до трех значащих цифр дает 565.

В случае округления по этапам, мы имеем:

1-й этап 565,46 округляем до 565,5;

2-й этап 565,5 округляем до 566 (ошибочный).

В.9 Построение поясняющих рисунков

На абсциссе от произвольной точки, в которой следует зафиксировать значение выбранного результата объема, вправо и влево отложить значение полученной погрешности для выбранного результата значения объема и из полученных точек на оси абсцисс провести вверх ординаты произвольной высоты, получив прямоугольник, наглядно отражающий разброс значений размера объема цилиндра от центральная ординаты, ограничиваемый пределами значений полученных погрешностей. Для того же цилиндра построить прямоугольник, отражающий разброс значений размера объема, от результата полученного с помощью второго средства измерений. При этом, наглядно отразить смещение по оси абсцисс полученного результата объема от выбранного, путем нахождения разницы между двумя имеющимися значениями объема одного и того же цилиндра с учетом знака (при положительной разнице значений - смещение вправо от выбранного, при отрицательной – влево). Полученной точке на оси абсцисс приписать значение, соответствующее результату значения объема, полученного с помощью второго средства измерений и от нее отложить вправо и влево значения погрешности, соответствующей результату значения объема, полученного с помощью второго средства измерений. Из полученных точек провести вверх ординаты до такого уровня, чтобы площадь полученного прямоугольника была равно площади, построенного ранее прямоугольника.