6.6.1. Цифровые вольтметры временного преобразования.

Р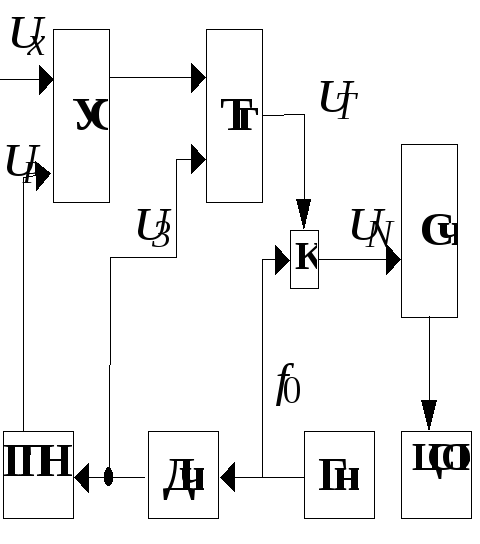абота ЦВ временного преобразования основана на преобразовании измеряемого напряжения в интервал времени и далее в цифровой код. ЦВВП делятся на вольтметры развертывающего ВП (ЦВР) и интегрирующие ЦВ (ИЦВ). В ЦВР измеряемое напряжениесравнивается с изменяющимся по линейному закону напряжением развертки, формируемым генератором пилообразного напряжения ГПН. Интервал времени от начала процесса развертки до момента равенства напряжений пропорционален напряжению.

И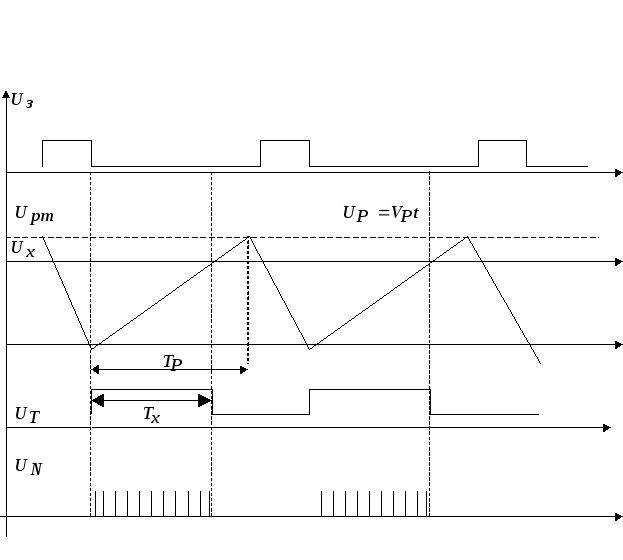мпульсызапуска, вырабатываемые генератором импульсов иДЧ, устанавливаютТгв единичное состояние и одновременно запускаютГПН, который формирует напряжение развертки, гдескорость изменения пилообразного напряжения;максимальное значение напряжения развертки;время развертки.

В момент равенства напряжений иустройство сравнения вырабатывает импульс, возвращающий триггер в нулевое состояние. На выходеТгформируется импульсдлительностью,

6.9. Цип с микропроцессорами.

Микропроцессор (МП) представляет собой устройство, состоящее из одной или нескольких микросхем, которое выполняет функции центрального процессора программируемой вычислительной машины. В общем случае МП состоит из арифметическо-логического устройства (АЛУ) и устройства управления (УУ). АЛУ служит для выполнения А и Л операций над данными, поступающими либо из памяти, либо из устройства ввода. УУ управляет потоком данных и команд согласно программе. Программа работы МП в виде набора отдельных команд и необходимые для вычисления данные хранятся во внешнем запоминающем устройстве (ЗУ). УУ выбирает из памяти команды, дешифрует и выполняет их, переключая соответствующие логические схемы, обеспечивая тем самым необходимую последовательность операций. Связь с внешними устройствами осуществляет устройство ВВ.

МП выполняет следующие функции:

 управление процессом АЦП;

 управление работой преобразователей различных физических величин в напряжение постоянного тока или код;

 автоматический выбор пределов измерения;

 управление приборным интерфейсом;

 управление индикатором;

 диагностику неисправностей;

 операции ввода–вывода;

 обработку измерительной информации;

 коррекция измерений;

 калибровка установки;

Появились логгеры (date loggersрегистраторы данных). Коммутаторы, АЦП, МП, или микро-ЭВМ, ОЗУ, ПЗУ, ЦСОИ, пульт оператора и УВВ. Несколько сот измерительных каналов.

6. Оценивание распределений.

6.1. Параметрическое и непараметрическое оценивание.

6.2. Гистограмма.

Чтобы получить более полное представление о распределении экспериментальных точек, обычно разбивают занятую ими область на интервалы (прямоугольники или параллелепипеды) и вычисляют чстоты попадания в эти интервалы (п., п-ды). Разделив эти частоты на длины интервалов (площади прямоугольников, объемы параллелепипедов) получают относительные плотности экспериментальных точек в соответствующих частях области, занятой экспериментальными точками. Полученное таким образом распределение экспериментальных точек можно изобразить графически, построив на каждом интервале прямоугольник, высота которого равна значению относительной плотности экспериментальных точек в этом интервале. Полученная в результате ступенчатая кривая называется гистограммой.

Н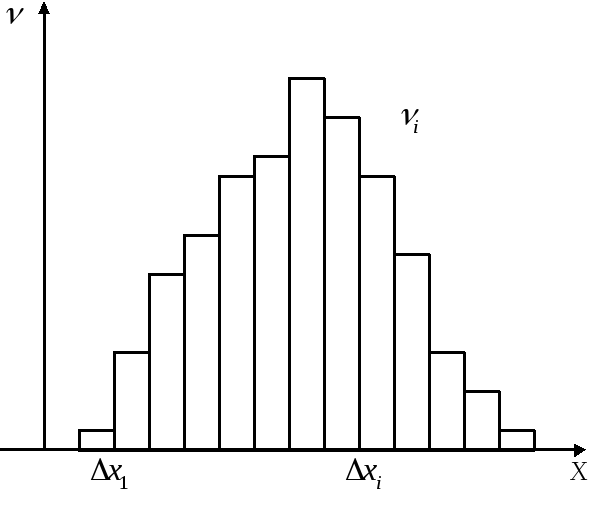адо выбирать так, чтобы в каждый интервал попадало не менее 10 эксперимен-тальных точек.

Если одновременно с построением гистограммы определяют выборочные средние, дисперсии и ковариации, то для упрощения вычислений обычно считают все экспериментальные точки в данном интервале совпадающие с его центром. Полученная таким образом новая выборка называется групповой выборкой.

Пусть  неизвестная плотность случайной величины . Предположим, что область возможных значенийразбита наинтервалов. Пустьслучайные числа попаданий величиныв интервалы:

Тогда частоты попаданий в интервалы будут:

(6.1)

И если , а значит ивелики, то можнопринять за оценки вероятностейи

(6.2)