Погрешность квантования

(5.2)

Закон распределения хихслучайный. В качестве уровней квантования лучше всего брать середины отрезков разбиения. (показать!)

В зависимости от способа преобразования ЦИП делятся на приборы прямого и уравновешивающего преобразования.

В ЦИП прямого преобразования отсутствует общая обратная связь. Они имеют очень большое быстродействие, но их точность высока только при высокой точности всех преобразователей.

ЦИП уравновешивающего преобразования охвачен общей обратной связью. Преобразователь обратной связи  ЦАП выходного дискретного сигнала в компенсирующую величину х_k одной физической природы с измеряемой величиной x(t). ЦАП изготавливается из элементов высокой точности и стабильности.

Бывают приборы развертывающего и следящего уравновешивания.

Для первого этапа значение компенсирующей величины в каждом цикле измерения возрастает от нуля ступенями, равными шагу квантования. При достижении равенства процесс уравновешивания прекращается, и фиксируется результат измерения, равный числу ступеней квантования компенсирующей величины. Отсчет показаний обычно производится в конце цикла.

Возникает динамическая погрешность _д.

Вприборах следящего уравновешивания уровень компенсирующей величины не возвращается к нулю, а остается постоянным. При изменении х отслеживается, чтобыне превышала значение шага квантования. Отсчет производиться или в момент уравновешивания или по внешним командам. Это сложнее в техническом отношении.

6.3. Дискретизация по времени и восстановление непрерывных функций.

Есть несколько способов дискретизации.

1. Переход от функции непрерывного времени к функции дискретного времени может быть выполнен путем взятия отсчетов функции в определенные дискретные моменты времени . По отсчетамможно восстановить другую функцию (искомую)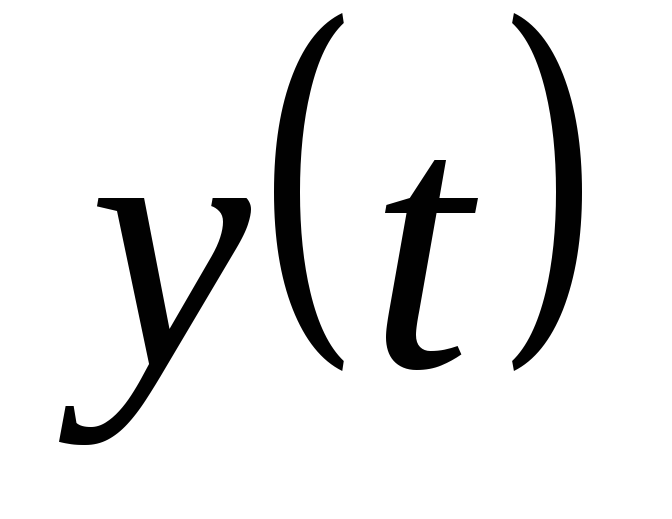, воспроизводящую исходную с заданной точностью. При дискретизации по времени одним из важнейших является вопрос о выборе шага дискретизации:

.

Существует оптимальный шаг дискретизации, который обеспечивает восстановление исходной функции с заданной точностью при минимальном числе отсчетов на конечном интервале времени.

2. Непрерывная функция на интервале наблюдениязаменяется конечным числом коэффициентов разложенияна выбранной системе базисных функций

Удобство этой системы.

Можно предположить, что точное восстановление исходной непрерывной функции во времени возможно лишь при . Однако существует широкий класс процессов, для которых возможно точное восстановление при конечном значении шага дискретизации. К данному классу относятся сигналы с ограниченным спектром.

6.3.1. Теорема Котельникова.

Если непрерывная функция удовлетворяет условиям Дирихле (ограничена, кусочно-непрерывна и имеет конечное число экстремумов), и ее спектр ограничен некоторой частотой(частота среза), то существует такой минимальный интервалмежду отсчетами, при котором имеется возможность безошибочно восстановить дискретизируемую функциюпо дискретным отсчетам. Этот максимальный интервал:

(6.5)

Основана теорема на возможности разложения функции в ряд:

(6.6)

функция отсчетов (6.7)

Т.е. функцию можно разложить по системе базисных функций. Причем коэффициенты разложениязначенияв дискретные моменты времени.

Свойства :

1. При max значение

2. При

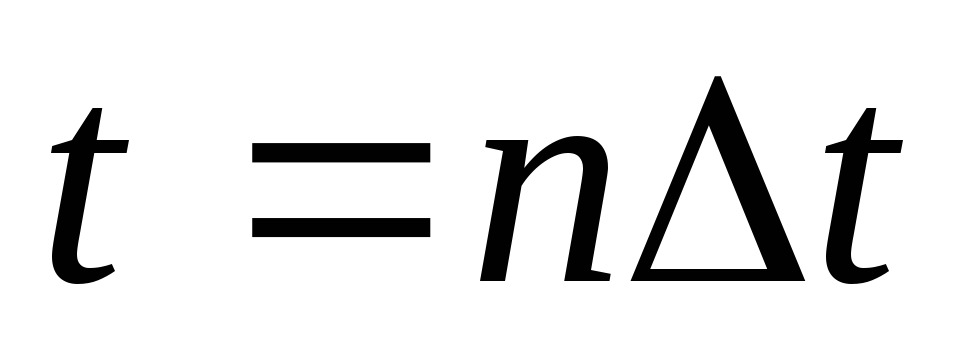
3. Функции ортогональны на бесконечно большом интервале времени.

Практическая ценность разложения функции в ряд Котельникова заключается в том, что каналу связи не передаются известные по виду функции отсчетов , а передаются только решетчатые функции.

С точки зрения практической реализации функция отсчетов полностью соответствует изменению во времени напряжения на выходе идеального фильтра нижних частот, одинаково пропускающего все частоты от 0 до , при подаче на его входимпульса.

В реальных условиях точное восстановление невозможно из-за того, что не выполняются условия теоремы Котельникова.

Реальные функция на конечных интервалах времени, поэтому их спектры бесконечные.

(6.8)