2.7 Расчет по образованию нормальных трещин

2.7.1 Стадия изготовления

Образование верхних (начальных) трещин при обжатии элемента проверяется из условия:

,

где 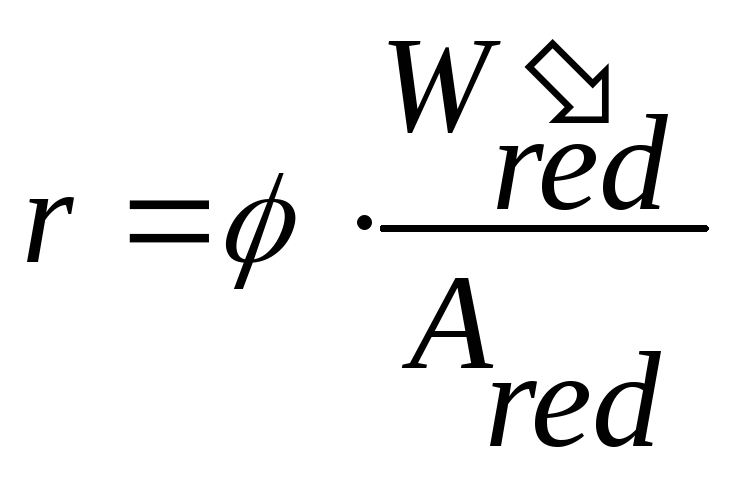- расстояние от центра тяжести приведенного сечения до нижней ядровой точки;

но - коэффициент, учитывающий неупругие деформации сжатого бетона и обусловленное ими уменьшение размеров ядра сечения;

- момент от собственного веса элемента; принимается со знаком «+», когда направления этого момента и момента усилия совпадают.

Усилие обжатия , эксцентриситет. Изгибающий момент от собственного веса для опасного сеченияc учетом коэффициента динамичности при подъеме .

.

Максимальное краевое напряжение в сжатом бетоне от действия собственного веса и усилия обжатия :

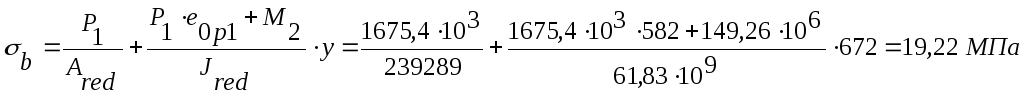
Тогда ;.

Проверяем условие:

, следовательно, в опасном сечении при подъеме балки не образуются начальные (верхние) трещины, в связи с чем расчет их раскрытия не требуется.

2.7.2 Стадия эксплуатации

Расчет по образованию нормальных трещин производится из условия:

,

где - изгибающий момент от внешних нагрузок с коэффициентом надежности по нагрузке:

- момент, воспринимаемый сечением при образовании нормальных трещин; здесь - момент усилия обжатия относительно ядровой точки сечения, наиболее удаленной от грани.

Усилие обжатия , эксцентриситет. Изгибающий момент для опасного сечения:.

Максимальное напряжение в крайнем сжатом волокне бетона (

):

.

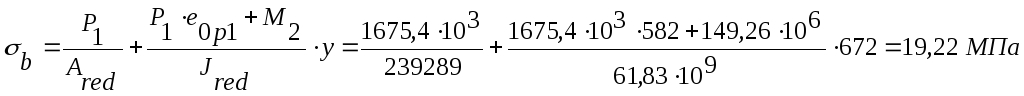
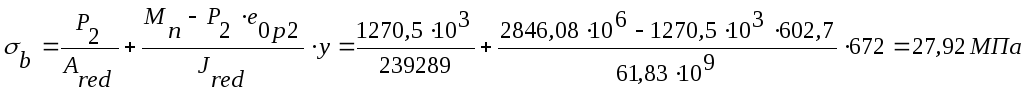Тогда ;.

Момент образования трещин:

.

При в стадии эксплуатации на нижней грани балки образуются нормальные трещины и необходимо выполнить расчет по их раскрытию.

2.8 Расчет по раскрытию нормальных трещин

2.8.1 Стадия эксплуатации

Вычисляем вспомогательные коэффициенты и параметры.

1. ;

;

;

;

;

;

;

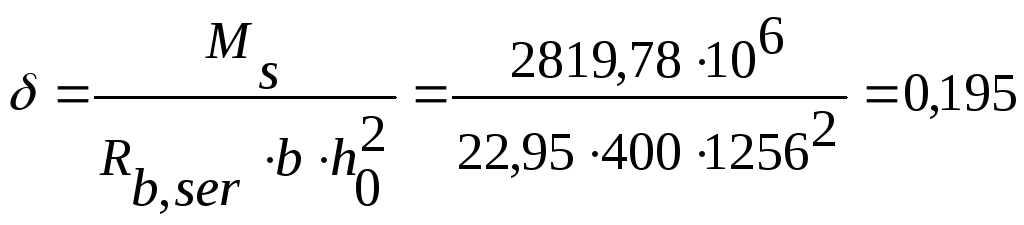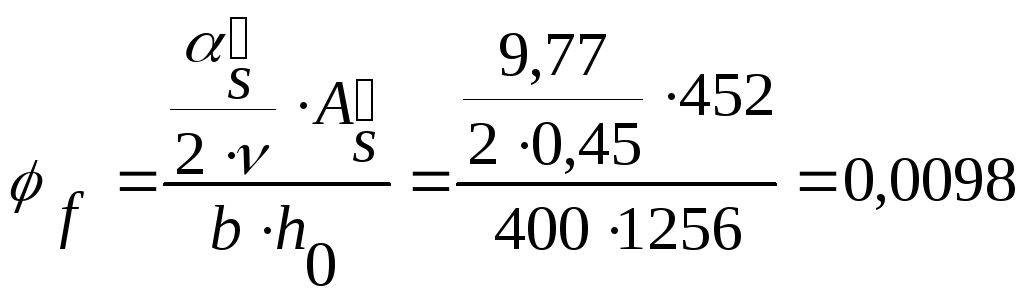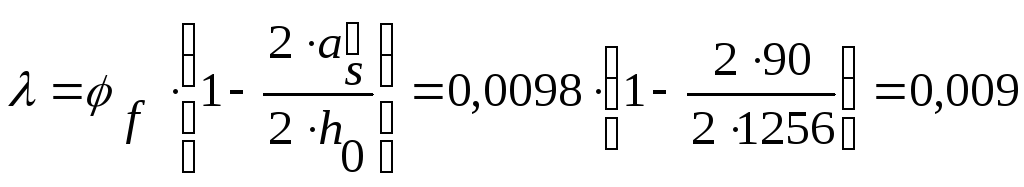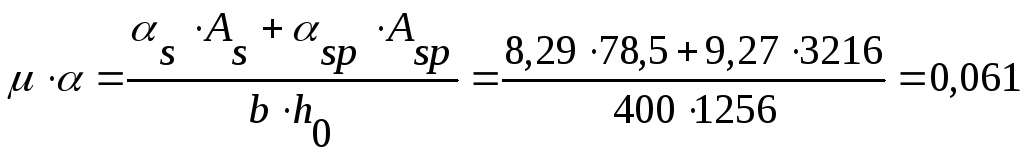2. Относительная высота сжатой зоны в сечении с трещиной:

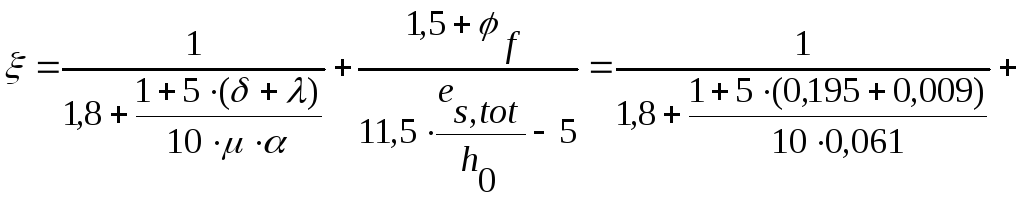
, принимаем .

3. Плечо внутренней пары сил в сечении с трещиной:

.

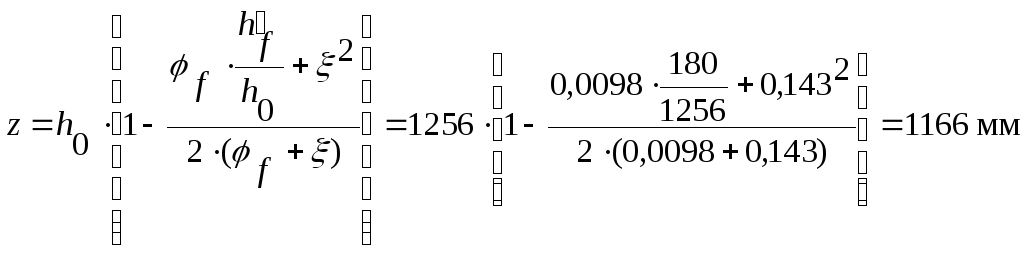4. Так как растянутая арматура расположена в два ряда по высоте сечения нижнего пояса, напряжения в ней определяем с учетом коэффициента равным:

.

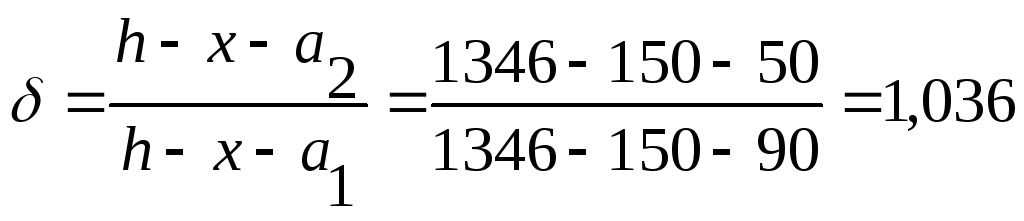5. Приращение напряжений в растянутой арматуре:

.

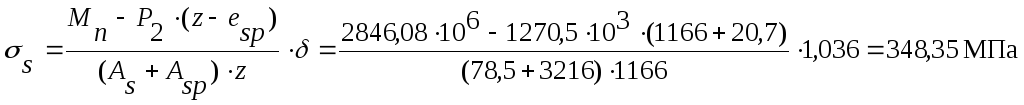6. Ширина непродолжительного раскрытия трещин:

,

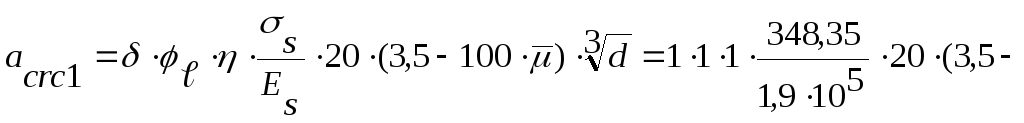
где .

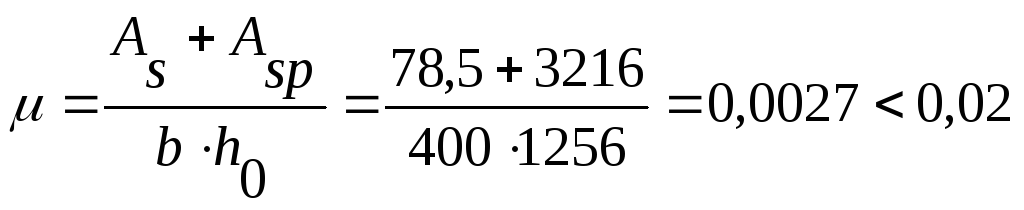3 Статический расчет поперечной рамы

3.1 Вычисление геометрических характеристик сечений колонн

Моменты инерции сечений двух колонн ряда А:

- надкрановой части ;

- подкрановая часть .

Коэффициенты для вычисления реакций:

;

;

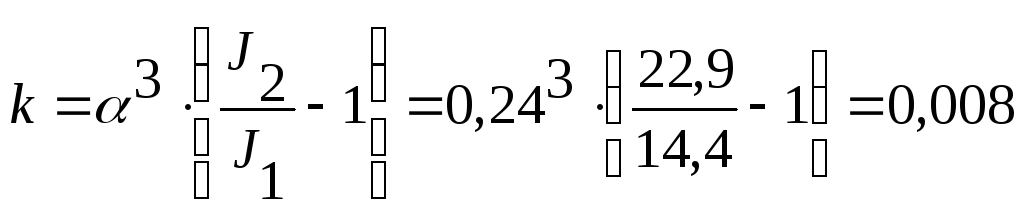смещение геометрических осей сечений подкрановой и надкрановой частей стойки – е = 210 мм.

Моменты инерции сечений колонны ряда Б:

- надкрановой части ;

- подкрановая часть .

Коэффициенты для вычисления реакций:

;

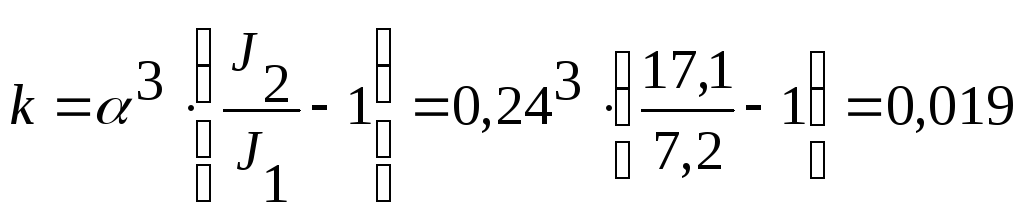смещение геометрических осей сечений подкрановой и надкрановой частей стойки – е = 0 мм.

3.2 Определение реакций верха колонн рамы-блока от единичного смещения

3.1.1 Определение усилий в стойке.

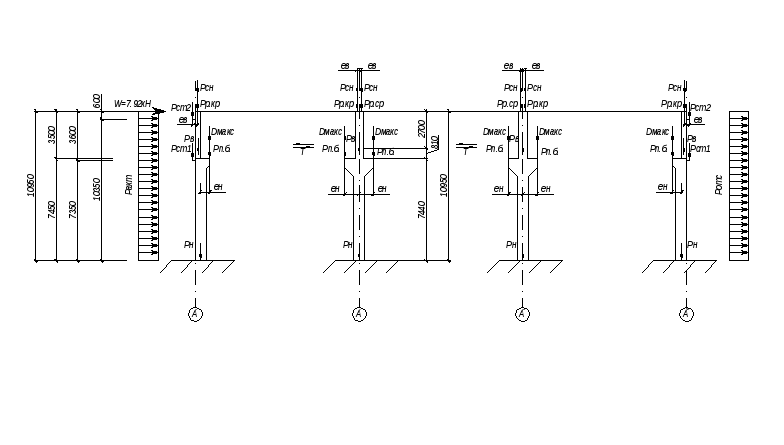
Статический расчет производится с помощью таблиц для расчета сборных железобетонных многопролетных по­перечников с ригелями в одном уровне.

Для выявления наибольших возможных усилий в сечениях стоек расчет поперечника производится отдельно от каждого вида загружения производятся расчеты от снеговой и крановой нагрузок, что позволяет вос­пользоваться ими в расчетах от постоянной нагрузки.

Благодаря симметрии поперечника относительно оси среднего пролета в расчете достаточно определить усилия от всех видов нагрузок только в стой­ках по осям А и Б. При расчете на ветровую нагрузку, для определения уси­лий в стойках по осям А и Б при направлении ветра слева направо и справа налево, целесообразно определить усилия во всех стойках при каком-либо одном направлении ветра, чтобы воспользоваться ими для определения усилий в стойках при другом направлении ветра.

Поперечник рассчитывается на следующие виды загружения: 1 – по­стоянная нагрузка; 2 – снеговая нагрузка на покрытии пролета АБ; 3 – снеговая нагрузка на покрытии пролета БВ; 4 – крановая нагрузка Dмакс, действующая на стойку по оси А; 5 – крановая нагрузка Dмакс, дей­ствующая на стойку по оси Б, со стороны пролета АБ; 6 – крановая на­грузка Dмакс, действующая на стойку по оси Б, со стороны пролета БВ; 7 – крановая нагрузка Т, действующая на стойку по оси А слева направо и справа налево; 8 – крановая нагрузка Т, действующая на стойку по оси Б слева направо и справа налево; 9 – ветровая нагрузка действующая слева направо; 10 – ветровая нагрузка, действующая справа налево.

Для подбора сечений стоек определяются наибольшие возможные усилия (изгибающий момент и продольная сила) в четырех сечениях стоек: в верхнем, в сечениях непосредственно выше и ниже подкрановой ступени и в нижнем. Для нижнего сечения стоек определяется также поперечная сила, необхо­димая для расчета фундаментов под стойки.

Стойка по оси А

Загружение 2. Снеговая нагрузка.

При n=0.63 λ=0.24 у_в=0, определяем по т. 16,1 /5/ k₁=1.546 и =1.392

Величину горизонтальной реакции R_b находим по формуле:

Определяем усилия в сечениях стойки:

Изгибающие моменты:

М₁=362,88·0,01=3,63 кН·м

М₂=362,88·0,01+6,56·3,5=26,6 кН·м

М₃=-362,88·0,2+6,56·3,5=-49,62 кН·м

М₄=-362,88·0,2+6,56·14,55=22,87 кН·м

Продольные силы N1=N2=N3=N4=-362.88 кН

Поперечная сила Q=6,56 кН.

Загружение 2 и эпюра изгибающих моментов.

Загружение 4. Крановая нагрузка.

При n=0.63, λ=0.24, у=1,0Н_н определяем по т. 16,2 /5/ k₂=1,393

Величину горизонтальной реакции R_b находим по формуле:

Определяем усилия в сечениях стойки:

Изгибающие моменты:

М₁=0

М₂=-14,28·3,5=-50 кН·м

М₃=426,25·0,35-14,28·3,5=99,19 кН·м

М₄=426,25·0,35-14,28·14,55=-58,6 кН·м

Продольные силы N1=N2=0 N3=N4=-426,25 кН

Поперечная сила Q=-14,28 кН.

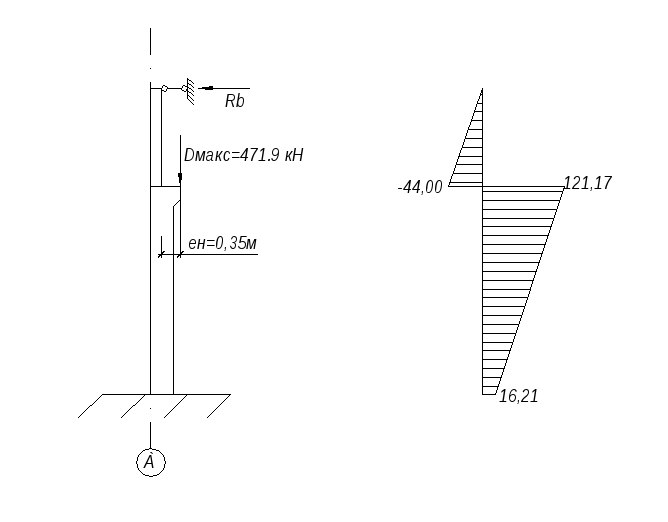
Загружение 4 и эпюра изгибающих моментов.

Загружение 1. Постоянная нагрузка.

Усилия в стойке от действия силы Р_р._кр получаем умножением усилий в стойке от Р_сн (загружение 2) на коэффициент:

k_1.2=Р_р.кр/Р_сн.=404,65/362,88=1,12

Усилия М и Q от действия силы Р_п.б получаем умножением усилий от Q_макс (загружение 4) на коэффициент:

k_1.4=Р_п.б/D_макс=105,6/426,25=0,248

Для определения усилий в стойке от собственного веса стен находим ве­личину горизонтальной реакции R_b . По табл. 16.1 /5/ для n = 0,63, λ = 0,24 и у = 0,2H_в

k_1а=1,538 и =1,393

Знак минус в данном случае показывает, что действительное направление усилия обратно обозначенному в табл. 16.1. /5/

Усилиями М и Q в стойке от собственного веса надкрановой части стойки пренебрегаем. Полные усилия в сечениях стойки от действия постоянной нагрузки находим как сумму усилий от отдельных воздействий:

Изгибающие моменты

М₁=0 кН·м

М₂=26,6·1,12-50·0,248+1,64·3,5-31,1·0,31=13,49 кН·м

М₃=-49,62·1,12+99,19·0,248+1,64·3,5-31,1·(0,31+0,21)=-41,41 кН·м

М₄=22,87·1,12-0,248·58,6+1,64·14,55-31,1·(0,31+0,21)=18,77 кН·м

Продольная сила

N₁=404,65 кН

N₂=404,65+31,1+14,63=450,38 кН

N₃=450,38+105,6=555,98 кН

N₄=555,98+75,06=631,04 кН

Поперечная сила

Q=6,56·1,12+14,28·0,248+1,64=12,53 кН.

Загружение 1 и эпюра изгибающих моментов.

Загружение 7. Крановая нагрузка T действует слева направо.

При n=0.63, λ=0.24, у=0,8Н_в определяем по т. 16,3 /5/ k₃=0,701

Величину горизонтальной реакции R_b находим по формуле:

Определяем усилия в сечениях стойки:

Изгибающие моменты:

М₁=0

М₂= М₃=-7,41·3,5+10,57·0,95=-15,9 кН·м

М₄=-7,41·14,55+10,57·10,95=7,93 кН·м

Изгибающие моменты в точке приложения силы Т

М=-7,41·2,7=-20 кН·м

Продольные силы

N1=N2=N3=N4=0 кН

Поперечная сила Q=-7,41+10,57=3,16 кН.

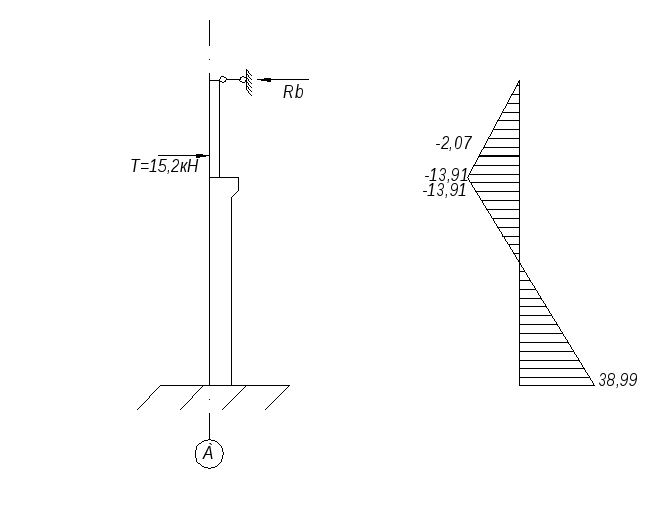
Загружение 7 и эпюра изгибающих моментов.

Стойка по оси Б.

Загружение 2. Снеговая нагрузка на покрытии пролета АБ.

При n=0.42, λ=0.24, у=1,0Н_н, е=0 определяем по т. 16,1 /5/ k₁=1,378

Величину горизонтальной реакции R_b находим по формуле:

Определяем усилия в сечениях стойки:

Изгибающие моменты:

М₁=362,88·(-0,2)=-72,58 кН·м

М₂=М₃=-362,88·0,2+6,87·3,5=-48,53 кН·м

М₄=-362,88·0,2+6,87·14,55=27,38 кН·м

Продольные силы N1=N2=N3=N4=-362.88 кН

Поперечная сила Q=6,87 кН.

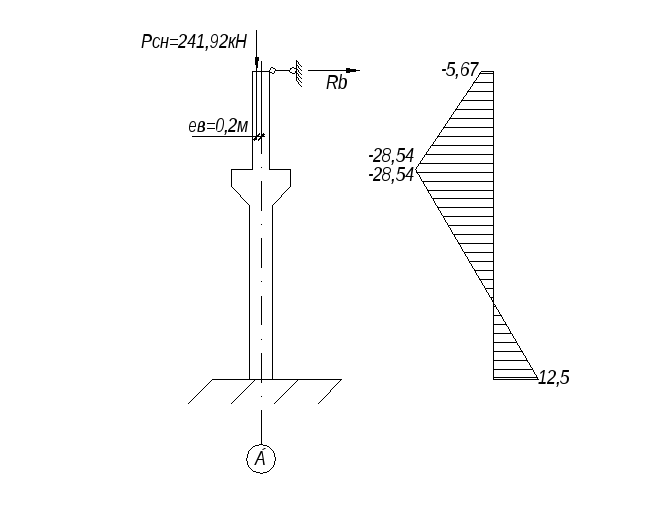
Загружение 2 и эпюра изгибающих моментов.

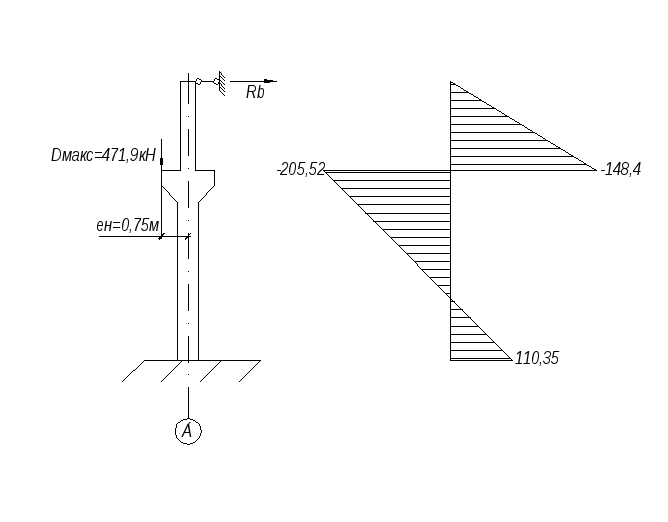
Загружение 5. Крановая нагрузка действует со стороны пролета АБ.

При n=0.42, λ=0.24, е=0.75, у=1,0Н_н определяем по т. 16,2 /5/ k₂=1,378

Величину горизонтальной реакции R_b находим по формуле:

Определяем усилия в сечениях стойки:

Изгибающие моменты:

М₁=0

М₂=30,3·3,5=106,05 кН·м

М₃=30,3·3,5-426,25·0,75=-213,64 кН·м

М₄=30,3·14,55-426,25·0,75=121,18 кН·м

Продольные силы N1=N2=0 N3=N4=-426,25 кН

Поперечная сила Q=30,3 кН.

Загружение 5 и эпюра изгибающих моментов.

Загружение 1. Постоянная нагрузка.

Благодаря симметрии точек приложения сил относительно P_p._cp оси стойки усилия М и Q =0

Продольная сила

N₁=809.3 кН

N₂=809.3+23.1=832.4 кН

N₃=832.4+2·105.6=1043.6 кН

N₄=1043.6+98.94=1142.54 кН

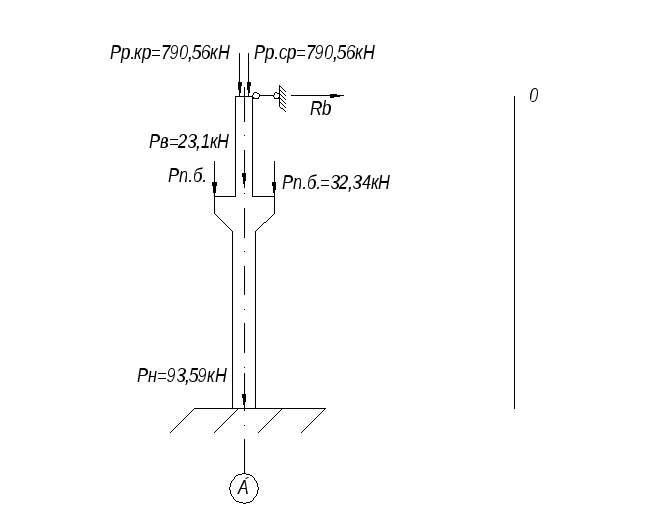
Загружение 1 и эпюра изгибающих моментов.

Загружение 8. Крановая нагрузка Т действующая справа налево.

При n=0.42, λ=0.24, у=0,8Н_в определяем по т. 16,3 /5/ k₃=0,691

Величину горизонтальной реакции R_b находим по формуле:

Определяем усилия в сечениях стойки:

Изгибающие моменты:

М₁=0

М₂= М₃=-7,3·3,5+10,57·0,95=-15,51 кН·м

М₄=-7,3·14,55+10,57·10,95=9,53 кН·м

Изгибающие моменты в точке приложения силы Т

М=-7,3·2,55=18,62кН·м

Продольные силы

N1=N2=N3=N4=0 кН

Поперечная сила Q=-7,3+10,57=3,27кН.

Загружение 8 и эпюра изгибающих моментов.

Загружение 9. Ветровая нагрузка действует справа налево.

При n=0.63, λ=0,24, определяем по т. 16,7 /5/ k₇=0,3728

Величину горизонтальной реакции R_b по оси А находим по формуле:

Величину горизонтальной реакции R_b по оси Г находим по формуле:

Усилие в дополнительной связи

R=ΣR_b+W=44.5+19.9=64.4 кН.

По т. 16,9 для n=0.63 λ=0,24 находим

k₉^кр=2,970 (для стоек по осям А и В)

По т. 16,9 для n=0.42 λ=0,24 находим

k₉^ср=2,935 (для стоек по оси Б)

Горизонтальные силы, приходящиеся на стойки по осям А и В.

Горизонтальные силы, приходящиеся на стойки по оси Б.

Определяем усилия в расчетных сечениях стоек.

Стойка по оси А.

Изгибающие моменты:

М₁=0 кН·м

М₂=М₃=(32,4-27,4)·3,5+5,05·3,5² /2=48,43 кН·м

М₄=(32,4-27,4)·14,55+5,05·14,55² /2=607,3 кН·м

Продольные силы N1=N2=N3=N4=0 кН

Поперечная сила Q=32,4-27,4+5,05·14,55=78,48 кН.

Стойки по оси Б.

М₁=0 кН·м

М₂=М₃=32·3,5=112 кН·м

М₄=32·14,55=456,6кН·м

Продольные силы N1=N2=N3=N4=0 кН

Поперечная сила Q=32 кН.

Стойка по оси В.

Изгибающие моменты:

М₁=0 кН·м

М₂=М₃=(32,4-17,1)·3,5+3,15·3,5² /2=72,84 кН·м

М₄=(32,4-17,1)·14,55+3,15·14,55² /2=556,05 кН·м

Продольные силы N1=N2=N3=N4=0 кН

Поперечная сила Q=32,4-17,1+3,15·14,55=61,13 кН.