МУ по ГИДРАВЛИКЕ

После открытия выходного крана вода приходит в движение и уровни воды в пьезометрах устанавливаются в соответствии с законами гидродинамики, как показано на рис. 2.2. При выполнении лабораторной работы измеряются пьезометрические высоты во всех пьезометрах и вычисляется

расход воды Q, который представляет собой определенный с помощью счетчика воды объем W, протекающий через любое живое сечение потока за единицу времени t:

Зная величину расхода, легко вычислить средние скорости V движения воды в тех живых сечениях, где установлены пьезометры:

где ω – площадь внутреннего поперечного сечения трубы; d − внутренний диаметр трубы.

Далее вычисляются скоростные высоты 2Vg2 для всех девяти сече-

ний. При этом можно принять 1,05 .

Плоскость сравнения для анализа уравнения Бернулли проводим на уровне оси симметрии трубопровода (см. рис. 2.2). При этом геометрические высоты во всех живых сечениях потока равны нулю (z = 0), а напор в

соседними пьезометрами равна разности напоров в начале и в конце участка. Гидравлический уклон для каждого участка вычисляется по формуле (2.4), пьезометрический – по формуле (2.5). Все результаты измерений и вычислений заносятся в табл. 2.1.

В табл. 2.1 l – расстояние между сечениями, в которых установлены пьезометры.

Заполнив табл. 2.1, необходимо вычертить на листе миллиметровой бумаги схему трубопровода и пьезометров (как показано на рис. 2.2), нанести на ней пьезометрические и скоростные высоты, построить напорную и пьезометрическую линии. Горизонтальный масштаб чертежа 1:20, вертикальный – 1:10. В заключение лабораторной работы следует проанализировать с помощью уравнения Бернулли причины изменения пьезометрических и скоростных высот, гидравлических и пьезометрических уклонов по длине трубопровода.

12

Таблица 2.1

Лабораторная работа № 3

РЕЖИМЫ ДВИЖЕНИЯ ЖИДКОСТИ

Цель работы:

1.Путем визуальных наблюдений убедиться в том, что жидкость может двигаться в двух принципиально разных режимах.

2.Ознакомиться с методикой расчетного определения режима движения жидкости.

Основные теоретические сведения

Существование двух принципиально разных режимов движения жидкости открыл в 1839 г. немецкий инженер-гидротехник Г. Хаген. В 1880 г. Д. И. Менделеев указал на то, что сопротивление движению жидкости зависит от режима движения. Следовательно, затраты энергии на движение жидкости, называемые в гидравлике потерями напора, тоже зависят от режима движения. Этим определяется значение открытия Г. Хагена.

13

В 1883 г. английский физик О. Рейнольдс завершил исследования, результаты которых создали основу современных представлений о режимах движения жидкости. Он провел эксперименты, которые позволяют визуально убедиться в том, что жидкость может двигаться в двух принципиально различных режимах, и понять физическую сущность этих режимов.

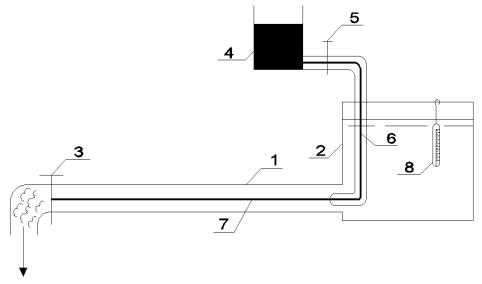
Лабораторная работа проводится на установке, аналогичной установке О. Рейнольдса. Ее главная часть – горизонтальная стеклянная труба 1 с прозрачными стенками (рис. 3.1). Во время опыта через трубу пропускается поток воды из бака 2. Скорость движения воды в трубе регулируется краном 3. Над баком с водой укреплен небольшой бачок 4 с концентрированным водным раствором красителя, который может подаваться в трубу 1 с помощью крана 5 и трубки 6. Для этого нижний горизонтальный конец трубки 6 с маленьким выходным отверстием введен в трубу 1.

Рис. 3.1. Схема установки для изучения режимов движения жидкости

При проведении опыта кран 3 немного приоткрывается, с тем чтобы вода в трубе 1 пришла в движение с очень небольшой скоростью. Одновременно приоткрывается кран 5 и в трубу 1 начинает поступать раствор красителя. Если скорость движения воды в трубе 1 достаточно мала, то раствор красителя образует в ней совершенно прямую линию 7 с четкими границами, параллельную стенкам трубы. Эта линия выглядит так, как будто ее провели рейсфедером по линейке. Если в трубу 1 подавать раствор красителя из нескольких трубок, то из каждой трубки протянется прямая окрашенная линия. Все эти линии будут параллельны между собой и стенками трубы. Очевидно, что при этом все частицы жидкости в трубе движутся по прямолинейным параллельным траекториям, жидкость в процессе движения не перемешивается, поток соответствует понятию струйной модели потока жидкости, т. е. его можно считать состоящим из эле-

14

ментарных струек, которые имеют непроницаемые границы и не изменяют свою форму во времени. Такой режим движения жидкости получил название ламинарного. Его главной чертой является отсутствие перемешивания жидкости при движении.

Ознакомившись с поведением жидкости при ламинарном режиме, постепенно приоткрывают кран 3, увеличивая таким образом скорость движения воды в трубе 1. В течение некоторого времени ламинарный режим сохраняется. Но по достижении некоторой величины скорости окрашенная струя 7 начинает деформироваться. Сначала она становится волнистой затем, по мере увеличения скорости, появляются разрывы, границы струи расплываются, и наконец струя полностью исчезает, а по трубе движется равномерно окрашенный поток.

Очевидно, что в данном случае в трубе 1 установился новый режим движения жидкости, принципиально отличающийся от ламинарного тем, что отдельные частицы жидкости движутся по сложным траекториям, струйная модель потока жидкости не наблюдается.

Такой режим движения жидкости называется турбулентным. Его основная черта – перемешивание жидкости в процессе движения. Скорости, при которых один из режимов движения сменяется другим, называются критическими. Эксперименты показали, что критическая скорость, при которой ламинарный режим переходит в турбулентный, больше, чем та, при которой турбулентный режим переходит в ламинарный. Поэтому первая из них получила название верхней критической скорости (Vкр.в), а вторая – нижней (Vкр.н):

Vкр.в > Vкр.н.

Экспериментальные и теоретические исследования О. Рейнольдса показали, что режим движения жидкости определяется не только скоростью, но и вязкостью жидкости, а также размерами и формой живого сечения потока. Ученый получил безразмерный параметр, который в настоящее время называется критерием или числом Рейнольдса и применяется для расчетного определения режима движения жидкостей:

где V – средняя скорость движения жидкости; R – гидравлический радиус живого сечения потока; ν – кинематический коэффициент вязкости жидкости.

Формула (3.1) применима для потоков с любой формой живого сечения. Но для круглоцилиндрических труб принято вместо гидравлического

15

радиуса использовать геометрический внутренний диаметр труб d. Поскольку для труб гидравлический радиус

В настоящее время считается, что границей между турбулентным и ламинарным режимом движения жидкости в круглоцилиндрических напорных трубах является число Рейнольдса Re = 2300, вычисленное по формуле (3.2). Поэтому для расчетного определения режима движения жидкости в напорном трубопроводе необходимо вычислить число Рейнольдса по формуле (3.2). Если Re < 2300 – режим ламинарный. ЕслиRe 2300 – режим турбулентный.

При проведении лабораторной работы сначала с помощью кранов 3 и 5 в трубе 1 устанавливается ламинарный режим движения (прямолинейная струя раствора красителя). Определяется расход воды по ее объему W, который накопится в измерительном сосуде за время t, измеренное секундомером:

Далее измеряется температура воды в баке 2 по термометру 8. По таблице, висящей на стене рядом с прибором, находят кинематический коэффициент вязкости, соответствующий измеренной температуре. В заключение вычисляется Re по формуле (3.2). Все эти данные заносятся в табл. 3.1. В последние графы таблицы записываются выводы о режиме движения по визуальным наблюдениям и по вычисленному Re.

Затем кран 3 приоткрывается до получения ясно выраженного турбулентного движения воды в трубе 1 (равномерно окрашенный поток), повторяются определение расхода, все последующие вычисления и заполняются все графы табл. 3.1.

16

Лабораторная работа № 4

ОПРЕДЕЛЕНИЕ ПОТЕРЬ НАПОРА ПО ДЛИНЕ ТРУБОПРОВОДА

Цель работы:

1.Опытное определение потерь напора по длине в круглоцилиндрической трубе при напорном установившемся равномерном движении воды.

2.Опытное определение коэффициента гидравлического трения.

3.Определение области гидравлического сопротивления трубопро-

вода.

4.Вычисление коэффициентагидравлического трения поэмпирической формуле для соответствующей области гидравлического сопротивления.

5.Вычисление толщины ламинарного пограничного слоя.

Основные теоретические сведения

Поток жидкости в трубопроводе затрачивает энергию на преодоление сил трения, которые возникают как в самой жидкости, так и между жидкостью и стенками трубопровода. Силы трения, преодолеваемые потоком, называются гидравлическими сопротивлениями. Поскольку удельная энергия жидкости, отнесенная к единице веса, именуется в гидравлике напором, затраты энергии на преодоление сил трения получили название

потерь напора.

Различают два вида гидравлических сопротивлений и обусловленных ими потерь напора: 1) потери по длине потока hl и 2) местные потери напора hм. Потери по длине в случае равномерного движения представляют собой затраты энергии на преодоление сопротивлений, равномерно распределенных по длине потока. Местные потери обусловлены локальными сопротивлениями, сосредоточенными на небольшом участке потока, например, на резком повороте, при вытекании жидкости из отверстия и т. п.

Полная потеря напора определяется суммированием потерь на отдельных участках и местных сопротивлениях:

17

В данной лабораторной работе определяется потеря напора по длине прямого горизонтального трубопровода (рис. 4.1) между сечениями 11 и 12 при напорном движении.

Рис. 4.1. Схема установки для изучения потерь напора по длине

Напорное движение возникает в условиях, когда труба заполнена жидкостью и гидродинамическое давление во всех точках жидкости выше атмосферного.

На участке 11–12 местные сопротивления отсутствуют. Поэтому hw = = hl и потеря напора hl может быть определена как разность напоров в сечениях 11 и 12:

Все обозначения пояснены в описании к лабораторной работе № 2. Согласно уравнению неразрывности потока, расход Q во всех сече-

ниях трубопровода одинаков. Площадь живого сечения потока тоже не изменяется по длине потока. Следовательно, средняя скорость движения во-

18

ниях одинаковы. Это означает, что движение воды в трубопроводе равномерное.

Для горизонтального трубопровода геометрические высоты во всех сечениях равны. Таким образом,

и уравнение (4.3) преобразуется в выражение

которое показывает, что в прямом напорном трубопроводе потеря напора по длине равна разности пьезометрических высот в начале и в конце рассматриваемого участка. Иными словами, при равномерном движении жидкости потери напора можно определять не только по напорной, но и по пьезометрической линии.

Итак, при проведении лабораторной работы опытное определение hl заключается в измерении разности пьезометрических высот в пьезометрах

11 и 12 (рис. 4.1).

Гидравлические сопротивления по длине в напорных трубопроводах характеризуются безразмерным коэффициентом гидравлического трения λ, который входит в формулу Вейсбаха – Дарси для вычисления потерь напора по длине:

Эта формула применяется в лабораторной работе для опытного определения

Чтобы воспользоваться формулой (4.7), необходимо определить расход воды в трубопроводе так же, как это делается в других лабораторных работах:

и по расходу вычислить среднюю скорость движения воды:

19

В инженерной практике коэффициент гидравлического трения чаще всего вычисляют по эмпирическим формулам. При этом приходится учитывать, что гидравлические сопротивления по длине сильно зависят от режима движения жидкости. Поэтому для различных режимов используются разные формулы, приведенные в табл. 4.1.

Таблица 4.1

которая выведена теоретическим путем.

При ламинарном режиме λ зависит только от числа Рейнольдса, т. е. определяется скоростью движения жидкости, внутренним диаметром трубопровода и вязкостью жидкости. Принципиально важно то, что λ не зависит от шероховатости стенок трубы. Потери напора по длине прямо про-

20