C

*

*

Дано

А; Ом; Ом;

Ом; Ом; Ом.

Определить

Показания вольтметра и ваттметра. Проверить баланс мощностей рис. 3.1.1.

W

R₁

X₁

X_M

V

~

A

X₂

A

R

R₂

B

Рис. 3.1.1

Решение

Найдем напряжение между точками А и В:

.

С другой стороны:

Тогда

.

Найдем напряжение между точками С и В:

Таким образом, показания вольтметра: U_V = 59,4 B.

Активная мощность цепи:

.

или

.

Таким образом, показания ваттметра: P_W = 192 Bт.

Реактивная мощность цепи:

.

или

.

Комплексная мощность цепи:

.

3.2

Дано

; ;R₁ = R₂ = 4 Ом;

R₃ = 2 Ом; X₁ =10 Ом; X₂ = 5 Ом;

X_C = 4 Ом; X_М = 5 Ом.

Определить

Все токи и напряжения между узлами А,В и В,С (рис. 3.2.1). Проверить баланс мощностей.

X_М

R₁

X₁

X₂

X_C

R₂

В

А

R₃

С

Рис. 3.2.1

Решение

В контурных токах система уравнений для электрической цепи

рис. 3.2.1 в матричной форме будет иметь вид:

.

Раскрытие главного определителя системы дает:

.

Произведя замену первого столбца в матрице коэффициентов, столбцовой матрицей свободных параметров получим:

Откуда

.

Произведя аналогичную замену для второго столбца в матрице коэффициентов, будем иметь:

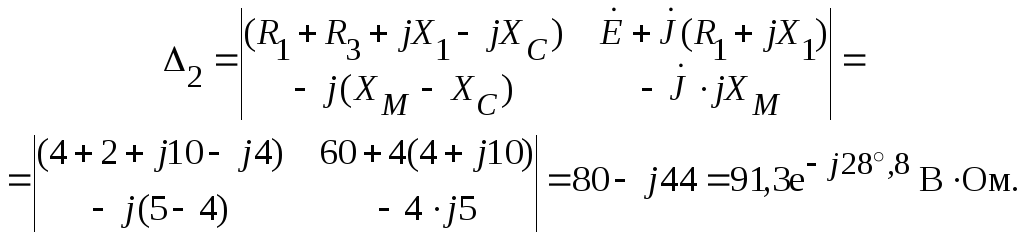
Тогда

.

Находим токи и:

;

.

Ищем напряжение между точками А и В:

или

Ищем напряжение между точками В и С:

.

или

Проверяем баланс мощностей.

Активная мощность цепи:

.

Реактивная мощность цепи:

Комплексная мощность цепи:

Расхождения в вычислениях незначительны.

3

.3

R₁

R₂

jX_M

Дано

; (ключK замкнут);

(ключ K разомкнут); .

K

jX_L1

jX_L2

Рис. 3.3.1

Определить

Параметры трансформатора R₁, R₂, X_L1, X_L2 и X_M (рис. 3.3.1). Построить векторную диаграмму.

Решение

Режим холостого хода (ключ Kразомкнут).

.

Таким образом, активное и реактивное сопротивления первичного контура соответственно равны: R₁ = 1 Ом; Х_L1 = 3 Ом.

Комплексное сопротивление взаимной индукции:

,

или X_M = 3 Ом.

Режим короткого замыкания (ключ К замкнут).

Для первичного и вторичного контуров, составим следующую систему уравнений:

Из первого уравнения системы находим ток I_КЗ2:

.

Подставив полученный результат во второе уравнение, запишем:

Таким образом, активное и реактивное сопротивления вторичного контура соответственно равны: R₂ = 9 Ом; Х_L2 = 3 Ом.

Векторную диаграмму (рис. 3.3.2) начинаем строить по уравнению для вторичной цепи. В соответствующем масштабе отложим вектор тока I_КЗ2. ВекторI_КЗ2 R₂ будет совпадать (по направлению) с векторомI_КЗ2. ВекторI_КЗ2jX_L2опережает вектор токаI_КЗ2на 90^о. ВекторI_1КЗjX_М, с учетом знака, будет замыкающим и направлен в начало координат. По векторуI_КЗ1jX_Мнаходим направление вектора тока первичной цепиI_КЗ1, который опережает векторI_КЗ1 jX_М на 90^о. Дальнейшее построение векторов первичной цепи в пояснениях не нуждается.

j

90^о

+

Рис. 3.3.2

3.4

Д

R₁

ано

jX_M

; R₁ = 100 Ом; X₁ = 10 Ом;

X₂ = 20 Ом; X_M = 10 Ом (рис. 3.4.1).

- jX_C

jX₂

jX₁

Рис. 3.4.1