Решение

Находим индуктивное сопротивление катушки:

.

Находим емкостное сопротивление конденсатора:

.

Полное сопротивление цепи:

.

Находим угол сдвига фаз ЭДС и тока:

.

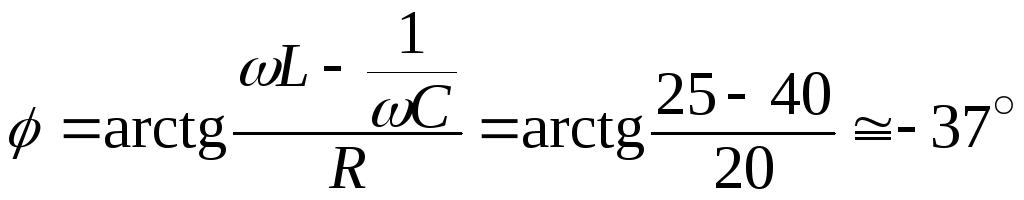Ток I равен:

.

Находим напряжение на активном сопротивлении:

или .

Напряжение на катушке индуктивности:

.

Напряжение на конденсаторе:

.

Реактивное сопротивление цепи (последовательное соединение катушки индуктивности и конденсатора):

.

Или .

Тогда напряжение на реактивном сопротивлении цепи:

, или .

Активная мощность:

, или .

Реактивная мощность:

.

Или .

Полная мощность:

, или .

Согласно выполненным расчетам в произвольном масштабе строим треугольники сопротивлений, напряжений и мощностей рис.1.3.2.

При X_L = X_C в электрической цепи (рис. 1.3.1) наступает резонанс напряжений, поскольку значения противоположных по фазе напряжений на индуктивности U_L и емкости U_C становятся равными.

1.4

Дано

Определить

Составляющие тока I. Построить треугольники проводимостей и токов.

Решение

Найдем полную проводимость цепи:

.

Находим активную проводимость:

.

Вычислим реактивную проводимость:

Находим угол сдвига фаз ЭДС и тока:

.

Находим активную составляющую тока:

, или .

Вычислим реактивную составляющую тока:

, или .

Согласно выполненным расчетам в произвольном масштабе строим треугольники проводимостей, и токов рис. 1.4.2.

1.5

Определить

Cоставляющие тока I. Построить треугольники проводимостей и токов.

Решение

Найдем полную проводимость цепи:

.

Находим активную проводимость:

.

Вычислим реактивную проводимость:

.

Находим угол сдвига фаз ЭДС и тока:

.

Находим активную составляющую тока:

, или .

Вычислим реактивную составляющую тока:

, или .

Согласно выполненным расчетам строим треугольники проводимостей, и токов (масштаб произвольный) рис. 1.5.2.

1.6

Рис. 1.6.1

R₁

E

X₁

Дано

X₂

R₃

E = 120 В; R₁ = 8 Ом; X₁ = -6 Ом; X₂ = 8,33 Ом; R₃ = 4 Ом; X₃ = 10 Ом.

X₃

Определить

Полные, активные и реактивные сопротивления (проводимости) всей цепи и всех ветвей рис. 1.6.1. Токи, напряжения и мощности. Проверить баланс мощностей. Построить векторную диаграмму напряжений и токов. Задачу решить аналитическим методом.

Решение

Найдем полные сопротивления каждой из трех ветвей цепи:

.

Активную и реактивную проводимости этих ветвей найдем по переходным формулам:

Полные проводимости первой и второй ветвей:

,или ;

,или .

Находим активную и реактивную проводимости параллельно соединенных ветвей:

G = G₁ + G₂ = 0,08 + 0 = 0,08 1/Ом; B = B₁ + B₂ = –0,06 + 0,12 = 0,06 1/Ом.

Полная проводимость параллельно соединенных ветвей:

.

При последовательном соединении разветвленного участка цепи и третьей ветви сопротивление всей цепи определится как сумма сопротивлений этих участков. Поэтому по переходным формулам вычислим активное и реактивное сопротивления разветвленного участка цепи:

Находим полное сопротивление разветвленного участка цепи:

.

Вычислим активное и реактивное сопротивление всей цепи:

Ом; Ом.

Находим полное сопротивление всей цепи:

.

Ток всей цепи (или ток в третьей ветви) равен:

Находим разность фаз между э.д.с. и током цепи:

.

Тогда напряжение третьей ветви:

B.

Вычислим активную и реактивную составляющие напряжения U₃:

.

В качестве проверки:

.

Расхождение (относительная ошибка) составляет ≈ 0,3% .

Находим разность фаз между напряжением U₃ и током I₃:

.

Найдем напряжение разветвленного участка цепи:

B.

Разность фаз между напряжением U и током I:

.

Находим токи первой и второй ветвей разветвленного участка:

, или A;

, или A.

Вычислим активные и реактивные составляющие этих токов:

.

.

В качестве проверки:

;.

Находим разность фаз между напряжением U и токами I₁ и I₂:

.

Определяем активную мощность всей цепи:

Вт .

Находим реактивную мощность всей цепи:

BAр .

Полная мощность всей цепи:

В×A .

Вычислим активную, реактивную и полную мощности первой ветви разветвленного участка:

;;.

Вычислим активную, реактивную и полную мощности второй ветви разветвленного участка:

;;

.

Вычислим активную, реактивную и полную мощности третьей ветви:

; ;.

Баланс мощностей:

P = P₁ + P₂ + P₃ Þ 432 = 288 + 0 + 144 Þ 432 Вт = 432 Вт;

Q = Q₁ + Q₂ + Q₃ Þ 576 = –216 + 432 + 360 Þ 576 вар = 576 BAр;

.

Векторную диаграмму рис. 1.6.2 строим в произвольно выбранном масштабе.

90°

–37°

68°,2

37°

53°,1

Рис. 1.6.2

1.7

I₁

Дано

А

В

Рис. 1.7.1

U₁

E

C₁

E = 120 B; R = 10×10³ Ом; P_R = 1 Вт; C₁ = 0,5×10^-6 Ф;

C₂ = 0,2×10⁻⁶Ф; f = 60 Гц.

C₂

U₂

R

I₃

I₂