5. Законы Ома и Кирхгофа в комплексной форме:

.

1.1

Д

ано

Рис. 1.1.1

R

C

u

i

По цепи рис. 1.1.1 протекает синусоидальный ток с амплитудой I_m = 1,41 А; f = 50 Гц; R = 100 Ом; C = 31,8×10^-6 Ф.

Определить

Вычислить мгновенные значения напряжений на резисторе, на конденсаторе, приложенного напряжения и мощности. Построить графики мгновенных значений тока, напряжений и мощности.

Решение

Поскольку в условии не оговаривается начальная фаза тока, то его мгновенное значение равно:

.

Мгновенное значение напряжения на резисторе:

B.

Мгновенное значение напряжения на конденсаторе:

Мгновенное значение приложенного напряжения:

Последнее выражение можно также получить, исходя из следующих рассуждений.

Полное сопротивление цепи равно:

Находим аргумент:

.

Поскольку j < 0, то приложенное напряжение u отстает от тока i по фазе на соответствующий угол.

Амплитуда приложенного напряжения:

.

Следовательно

Находим мгновенную мощность цепи:

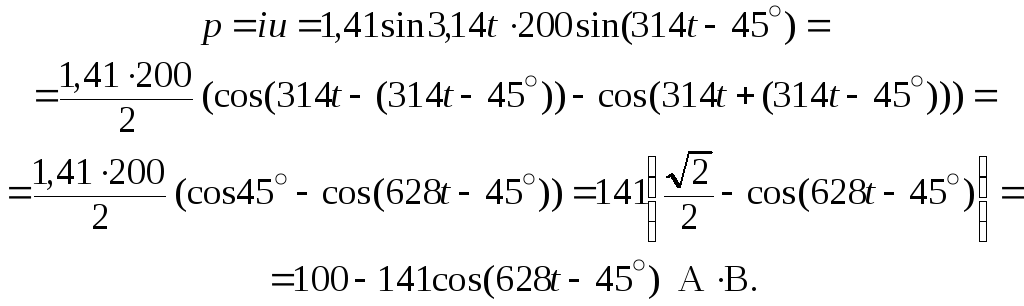
Графики мгновенных значений, построенные в произвольном масштабе, приведены на рис. 1.1.2.

Из графика видно, что ток i и напряжение на активном сопротивлении совпадают по фазе, а напряжениена конденсаторе отстает от токаi на 90^о.

1.2

Д

ано

e = 141sinwt; R₁ = 3 Ом; R₂ = 2 Ом; w = 314 1/c; L = 9,55×10^-3 Гн.

Определить

Ток и напряжение на элементах схемы рис. 1.2.1, методами комплексных амплитуд и мгновенных величин. Проверить баланс мощностей. Построить векторную диаграмму.

Решение

Для мгновенного и действующего значений ЭДС справедливы соотношения:

.

Находим комплексное сопротивление цепи:

.

Находим модуль и аргумент комплексного числа:

.

Откуда

.

Тогда комплексное действующее значение тока:

.

Комплексное действующее значение напряжения на сопротивлении R₁:

.

Комплексное действующее значение напряжения на сопротивлении R₂:

.

Комплексное напряжение на индуктивности:

Таким образом, напряжение на индуктивности опережает ток на угол 90^о:

.

Согласно закону Ома мгновенное значение тока:

,

где

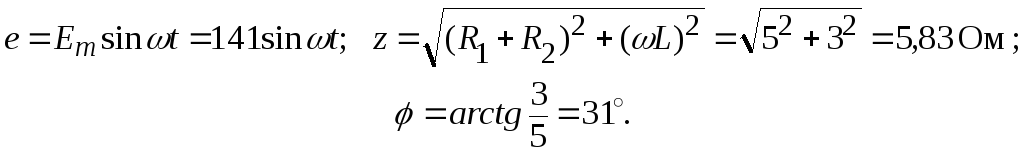
Тогда

.

Амплитудное значение тока:

.

Откуда

А.

Находим мгновенное значение напряжения на сопротивлении R₁:

B.

Находим мгновенное значение напряжения на сопротивлении R₂:

B.

Мгновенное значение напряжения на индуктивности:

Таким образом, напряжение на индуктивности опережает ток на угол 90^о.

Баланс мощностей следует из закона сохранения энергии, т.е. сумма всех отдаваемых мощностей равна сумме всех потребляемых мощностей:

,

где  - комплексная мощность;

P - активная мощность;

Q - реактивная мощность;

- комплексно – сопряженная величина.

;

.

Здесь ;.

Таким образом, с незначительной погрешностью активная и реактивная мощности совпадают с вещественной и мнимой частями комплексной мощности.

На комплексной плоскости строим векторную диаграмму рис.1.2.2.

1.3

Определить

Действующий ток I, угол сдвига фаз между ЭДС источника и тока, напряжение на элементах схемы. Построить треугольники сопротивлений, напряжений и мощностей.