6. Пример оформления титульного листа отчета

ПО ЛАБОРАТОРНЫМ РАБОТАМ

ПРИЛОЖЕНИЕ 8

ФЕДЕРАЛЬНОЕ АГЕНТСТВО ЖЕЛЕЗНОДОРОЖНОГО ТРАНСПОРТА

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ

ВЫСШЕГО ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ

«ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ПУТЕЙ СООБЩЕНИЯ ИМПЕРАТОРА АЛЕКСАНДРА I»

Факультет Экономика и менеджмент

Кафедра «Экономика и менеджмент в строительстве»

Отчет

по лабораторным работам дисциплины

УПРАВЛЕНИЕ ЗАТРАТАМИ ПРЕДПРИЯТИЯ (ОРГАНИЗАЦИИ)

Выполнил: _________________________________

(Фамилия И.О.)

студент____ курса _____ направ. подг.___________

группа__________

Подпись:________

Преподаватель: _____________________________

(Фамилия И.О.)

Оценка:_______________ Дата:_________________

Подпись: ________

Санкт-Петербург

20__

7. МЕТОДИЧЕСКИЙ ПРИМЕР ВЫПОЛНЕНИЯ ЛАБОРАТОРНОЙ РАБОТЫ

ПРИЛОЖЕНИЕ 9

Методический пример выполнения лабораторной работы №1

На примере Варианта № 8 – СМУ 1, 2, 4, 6.

Ход работы: необходимо в новой книге Excel создать на отдельном листе таблицу с исходными данными следующего вида:

Основная таблица Вспомогательная табл.

			Y	X1	X2	X3	X4	X5	X6		ср.числ.раб.	ср.числ.раб.сдел.	ср.числ.раб. всего	V.смр
сму1	1	январь	57,46	88,24	60,00	95,00	20,00	20,00	12,00		170	150	153	8792
	2	февраль	55,26	88,24	60,40	96,00	16,00	20,50	12,50		170	150	152	8400
	3	март	53,99	88,30	61,00	96,50	12,50	24,00	11,50		171	151	153	8260
	4	апрель	56,27	88,30	61,80	100,50	9,40	27,00	11,00		171	151	153	8610
	5	май	56,18	88,57	63,20	105,00	7,20	29,00	10,50		175	155	157	8820
	6	июнь	68,73	89,19	65,00	110,00	5,10	30,00	10,00		185	165	166	11410
	7	июль	66,63	89,19	67,80	113,00	3,10	30,50	10,00		185	165	166	11060
	8	август	71,19	89,47	70,00	116,00	1,30	31,00	10,50		190	170	177	12600
	9	сентябрь	96,86	89,47	71,30	117,00	1,00	31,40	8,00		190	170	172	16660
	10	октябрь	102,47	89,19	72,10	117,60	0,90	31,60	9,00		185	165	166	17010
	11	ноябрь	73,20	88,24	72,50	118,00	0,80	31,70	9,50		170	150	153	11200
	12	декабрь	79,61	88,82	73,00	118,20	0,70	31,80	8,10		170	151	153	12180
сму2	13	январь	42,94	88,89	65,00	95,00	20,00	23,00	11,00		180	160	163	7000
	14	февраль	39,51	88,89	65,30	95,50	15,90	23,80	10,50		180	160	163	6440
	15	март	33,29	88,89	66,00	97,00	13,00	26,00	10,00		180	160	164	5460
	16	апрель	39,70	89,01	66,90	99,00	10,20	28,00	9,50		182	162	164	6510
	17	май	44,12	88,65	69,10	101,50	7,70	31,00	9,00		185	164	165	7280
	18	июнь	54,44	88,42	71,00	105,50	5,40	31,50	8,50		190	168	171	9310
	19	июль	73,91	88,42	73,80	109,60	3,20	31,60	8,00		190	168	172	12712
	20	август	102,35	90,26	75,00	112,40	1,80	31,80	8,50		195	176	177	18116
	21	сентябрь	108,76	90,26	76,40	114,00	1,80	32,00	8,00		195	176	177	19250
	22	октябрь	90,06	89,47	77,20	114,60	1,70	33,00	7,50		190	170	171	15400
	23	ноябрь	77,78	88,89	77,60	114,80	1,60	33,50	7,00		180	160	162	12600
	24	декабрь	91,47	87,88	81,00	114,80	1,80	34,00	6,30		165	145	150	13720
сму4	25	январь	58,01	90,00	64,00	99,00	12,00	20,00	10,00		200	180	181	10500
	26	февраль	54,44	90,00	64,20	99,30	10,00	20,40	8,00		200	180	180	9800
	27	март	56,92	90,10	65,10	101,10	8,40	21,70	9,00		202	182	182	10360
	28	апрель	56,45	90,20	66,00	103,20	7,30	25,00	7,00		204	184	186	10500
	29	май	80,00	90,00	67,40	105,70	7,00	28,00	8,00		210	189	189	15120
	30	июнь	71,09	89,77	70,00	109,80	6,50	29,50	7,00		215	193	193	13720
	31	июль	87,77	89,77	72,00	113,70	6,00	31,00	5,00		215	193	193	16940
	32	август	118,51	90,00	74,00	116,50	5,10	30,00	2,00		220	198	202	23940
	33	сентябрь	142,03	90,22	75,20	118,00	4,30	31,00	3,00		225	203	207	29400
	34	октябрь	131,49	90,50	73,90	118,00	4,80	33,00	2,00		200	181	181	23800
	35	ноябрь	173,70	90,00	75,50	118,80	5,00	29,00	1,90		180	162	162	28140
	36	декабрь	82,35	88,24	80,00	118,80	7,00	27,00	1,50		170	150	153	12600
сму6	37	январь	62,30	90,48	68,00	105,00	24,00	15,00	9,00		210	190	191	11900
	38	февраль	58,33	90,43	68,40	105,60	21,40	15,50	9,00		209	189	192	11200
	39	март	60,93	90,48	69,30	107,00	18,30	16,50	9,00		210	190	193	11760
	40	апрель	62,06	90,57	70,10	109,10	15,50	18,00	7,00		212	192	194	12040
	41	май	78,52	90,23	71,70	111,60	13,00	20,00	8,00		215	194	194	15232
	42	июнь	84,85	90,00	63,80	115,40	11,10	22,50	7,00		220	198	198	16800
	43	июль	86,26	90,00	75,90	119,50	9,30	25,50	7,50		220	198	198	17080
	44	август	117,00	90,67	78,00	122,40	8,40	27,50	25,00		225	204	207	24220
	45	сентябрь	142,72	90,22	79,50	124,00	12,00	29,00	2,00		225	203	206	29400
	46	октябрь	114,75	91,50	70,00	124,50	15,00	28,00	1,00		200	183	183	21000
	47	ноябрь	140,85	90,00	80,60	124,70	18,00	28,50	1,50		180	162	164	23100
	48	декабрь	118,18	88,24	81,00	124,70	22,50	28,00	2,00		170	150	154	18200

Для расчета Y, Х1 и Х2 целесообразно составить справа от основной таблицы вспомогательную таблицу. Шапка основной таблицы, номера СМУ, месяцы, значения Х2, Х3, Х4, Х5, Х6 набираются вручную. Для расчета Y и Х1 в первую ячейку основной таблицы необходимо впечатать следующие формулы:

- для столбца Y: [ =V.смр/ ср.числ.раб. всего ];

- для столбца Х1: [ = ср.числ.раб.сдел./ ср.числ.раб.].

Далее необходимо скопировать формулы для столбцов Y и X1 следующим образом. Выделив одним щелчком левой кнопкой мышки ячейку с формулой, необходимо левой кнопкой мышки захватить правый нижний угол ячейки (появится черный крестик) и протащить вертикально вниз по столбцу до последнего наблюдения. Повторить данную операцию для Y и X1.

1. Проведение многошагового корреляционно-регрессионного анализа с применением средств Excel.

Примечание: при выполнении работы используются инструменты «Пакета анализа» Excel «Корреляция» и «Регрессия». При этом, в учебных целях, в работе используются не все показатели, рассчитанные с помощью названных инструментов. При использовании инструмента «Корреляция» в работе используются коэффициенты корреляции, рассчитанные с помощью данного инструмента. При использовании инструмента «Регрессия» в работе используются коэффициенты регрессии и прогнозные значения результирующего признака. Все остальные показатели, необходимые для достижения поставленных в работе целей, должны быть рассчитаны с помощью формул, которые приведены в методических указаниях к выполнению работы.

Для целей анализа используется линейная модель множественной регрессии вида:

Вм = а₀ + а₁х₁ + а₂х₂ + … а_nx_n, где

Вм – месячная выработка рабочего;

а₀ – свободный член уравнения (характеризует постоянную «нераспределенную» часть Вм вне зависимости от воздействия факторных признаков);

а₁…а_n – коэффициенты регрессии, характеризующие изменение выработки от изменения каждого факторного признака на единицу фиксированных значений остальных факторов;

x₁…x_n – факторные признаки (независимые переменные).

1.1. Построение корреляционной матрицы с помощью средств пакета анализа программного продукта Excel.

Для построения корреляционной матрицы необходимо зайти в меню Сервис выбрать Анализ данных*:

* Если эта команда недоступна, загрузите пакет анализа:

1. В меню Сервис выберите команду Надстройки (см. предыдущий рисунок).

2. В списке надстроек выберите Пакет анализа и нажмите кнопку OK.

3. Выполните инструкции программы установки, если это необходимо.

Далее в Анализ данных выбрать Корреляция и нажать ОК:

Нажмите на кнопку справа от ячейки Входной интервал:

Мышкой выделите весь массив данных Y и Х (нажать левой кнопкой мыши на верхнее левое значение Y и не отпуская протащить до последнего значения X6):

и нажмите Ввод, после чего в окне Корреляция появится входной интервал:

Нажмите ОК. После этого на новом рабочем листе (Лист 1) появится таблица следующего вида:

Столбцу 1 соответствует Y, Стобец 2 – Солбец 7 соответствует Х1 – Х6 соответственно.

Переименуйте столбцы и строки:

Переименуйте Лист 1 в Корреляция (быстрый двойной щелчок левой кнопкой мыши внизу на закладке Лист 1, и впечатать новое название закладки):

2. На основе расчетных значений коэффициентов корреляции корреляционной матрицы, полученных в ходе выполнения пункта 1., следует оценить их статическую значимость и проверку наличия мультиколлинеарности. Отбор независимых переменных для исключения их из дальнейшего анализа производится если:

• теснота связи Rxx≥0,85 (в этом случае одна из независимых переменных, связь которой с зависимой слабее, исключается);

В данном примере такие связи отсутствуют

Знак коэффициента корреляции Ryx не отвечает известному экономическому содержанию связи между зависимой и независимой переменными (или студент испытывает затруднения с интерпретацией полученной связи);

В данном примере исключаем Х5, так как связь XY должна быть со знаком «минус», в расчетной таблице – плюс

• теснота статистической связи Ryx статически несущественна.

Для оценки значимости коэффициента корреляции r используют t-критерий Стьюдента, который применяется при t-распределении, отличном от нормального.

При линейной однофакторной связи t-критерий можно рассчитать по формуле:

,

где (n - 2) – число степеней свободы при заданном уровне значимости α и объеме выборки n.

Полученное значение t_расч сравнивают с табличным (Приложение №4) значением t-критерия (для α = 0,05 с n-2 степенями свободы). Если рассчитанное значение t_расч превосходит табличное значение критерия t_табл, то практически невероятно, что найденное значение обусловлено только случайными колебаниями (то есть отклоняется гипотеза о его случайности).

На закладке Корреляция 1 вводим формулу для значений t-критерия кроме исключенных ранее факторов, как показано на рисунке:

Затем копируем формулу для остальных значений t-критерия (аналогично копированию в исходных данных для Y и Х1).

Сравните полученные значения t c t табличным (для данного варианта – 1,68).

Таким образом исключаются Х4 и Х5.

После проведения корреляционного анализа, в соответствии с пунктами 1- 2 количество факторных признаков, которые будут использоваться в дальнейшей работе может сократиться.

3. Построение множественной регрессии с помощью средств пакета анализа программного продукта Excel.

Для построения множественной регрессии необходимо исключить из исходных данных исключенные факторы. Необходимо в закладке с исходными данными выделить исключаемые столбцы (нажать на названия столбцов мышкой) и удалить их (правой кнопкой на названии столбцов - Удалить)

или захватив оба столбца за шапку левой кнопкой мыши перетащить их правее, и затем удалить пустые столбцы как показано выше.

В результате будет получена таблица исходных данных:

Зайдите в меню Сервис – Анализ данных – Регрессия

Нажмите кнопу справа от ячейки Входной интервал Y, выберите мышкой все значения Y, нажмите Ввод;

Нажмите кнопу справа от ячейки Входной интервал Х, выберите мышкой все значения Х , нажмите Ввод.

Во входных интервалах появились значения как показано на рисунке:

Нажмите ОК

Откроется новый лист следующего вида

Переименуйте полученный лист Регрессия 1 (двойной щелчок на закладке внизу экрана).

4. В целях возможного отсева грубых погрешностей, анализируются отклонения фактических значений зависимой переменной Y от прогноза по регрессии. Если данное отклонение превышает тройное среднеквадратическое отклонение уравнения регрессии, то данное наблюдение необходимо исключить, после чего вновь выполняется построение регрессии.

Среднеквадратическое отклонение необходимо рассчитать по формуле:

,

где n – количество наблюдений,

y – значения результирующего признака в соответствии с исходными данными,

- прогнозное значения результирующего признака.

Исключение наблюдений производится до тех пор, пока фактическое значение переменной Y от прогноза по регрессии не будет превышать тройное среднеквадратическое отклонение по уравнению регрессии.

Дополните лист Регрессия 1 таблицей следующего вида:

Данная таблица предназначена для расчета тройнго среднеквадратического отклонения уравнения регрессии (3 СКВО) и сравнения его с отклонениями фактических значений зависимой переменной Y (Отклонение)

Далее представлены формулы для каждого столбца данной дополнительной таблицы:

Столбец Y факт заполняется из исходных данных согласно показанной ниже формуле. Затем формула копируется вертикально вниз:

Столбец Y прогноз заполняется по формуле Вм = а₀ + а₁х₁ + а₂х₂ + … а_nx_n. Коэффициенты были рассчитаны ранее в результате расчета регрессии и находятся на данном листе выше.

Столбец Отклонение – разница между столбцами Y факт и Y прогноз

Столбец Отклонение в квадрате:

Затем суммируйте Отклонение в квадрате

Рассчитайте среднеквадратичное отклонение:

Рассчитайте тройное среднеквадратичное отклонение

Сравните полученное тройное среднеквадратичное отклонение с отклонениями. В результате отсеивается наблюдение №35 (61>49,79):

Удалите из исходных данных наблюдение № 35 и повторите построение регрессии и проверку:

Новый массив исходных данных с удаленным наблюдением № 35 необходимо разместить на новом листе Регрессия 2 (скопировать с листа исходные данные и удалить наблюдение № 35).

		Y	X1	X2	X3	X6
1	январь	57,46	88,24	60,00	95,00	12,00
2	февраль	55,26	88,24	60,40	96,00	12,50
3	март	53,99	88,30	61,00	96,50	11,50
4	апрель	56,27	88,30	61,80	100,50	11,00
5	май	56,18	88,57	63,20	105,00	10,50
6	июнь	68,73	89,19	65,00	110,00	10,00
7	июль	66,63	89,19	67,80	113,00	10,00
8	август	71,19	89,47	70,00	116,00	10,50
9	сентябрь	96,86	89,47	71,30	117,00	8,00
10	октябрь	102,47	89,19	72,10	117,60	9,00
11	ноябрь	73,20	88,24	72,50	118,00	9,50
12	декабрь	79,61	88,82	73,00	118,20	8,10
13	январь	42,94	88,89	65,00	95,00	11,00
14	февраль	39,51	88,89	65,30	95,50	10,50
15	март	33,29	88,89	66,00	97,00	10,00
16	апрель	39,70	89,01	66,90	99,00	9,50
17	май	44,12	88,65	69,10	101,50	9,00
18	июнь	54,44	88,42	71,00	105,50	8,50
19	июль	73,91	88,42	73,80	109,60	8,00
20	август	102,35	90,26	75,00	112,40	8,50
21	сентябрь	108,76	90,26	76,40	114,00	8,00
22	октябрь	90,06	89,47	77,20	114,60	7,50
23	ноябрь	77,78	88,89	77,60	114,80	7,00
24	декабрь	91,47	87,88	81,00	114,80	6,30
25	январь	58,01	90,00	64,00	99,00	10,00
26	февраль	54,44	90,00	64,20	99,30	8,00
27	март	56,92	90,10	65,10	101,10	9,00
28	апрель	56,45	90,20	66,00	103,20	7,00
29	май	80,00	90,00	67,40	105,70	8,00
30	июнь	71,09	89,77	70,00	109,80	7,00
31	июль	87,77	89,77	72,00	113,70	5,00
32	август	118,51	90,00	74,00	116,50	2,00
33	сентябрь	142,03	90,22	75,20	118,00	3,00
34	октябрь	131,49	90,50	73,90	118,00	2,00
36	декабрь	82,35	88,24	80,00	118,80	1,50
37	январь	62,30	90,48	68,00	105,00	9,00
38	февраль	58,33	90,43	68,40	105,60	9,00
39	март	60,93	90,48	69,30	107,00	9,00
40	апрель	62,06	90,57	70,10	109,10	7,00
41	май	78,52	90,23	71,70	111,60	8,00
42	июнь	84,85	90,00	63,80	115,40	7,00
43	июль	86,26	90,00	75,90	119,50	7,50
44	август	117,00	90,67	78,00	122,40	25,00
45	сентябрь	142,72	90,22	79,50	124,00	2,00
46	октябрь	114,75	91,50	70,00	124,50	1,00
47	ноябрь	140,85	90,00	80,60	124,70	1,50
48	декабрь	118,18	88,24	81,00	124,70	2,00

Выполнить регрессию на том же листе (Регрессия 2), что и новые исходные данные, для чего при построении регрессии выбрать выходной интервал на данном листе, выбрать Интервал Y и Интервал Х как показано на рисунке:

Будет получена регрессия следующего вида:

Добавьте столбцы между исходными данными и регрессией:

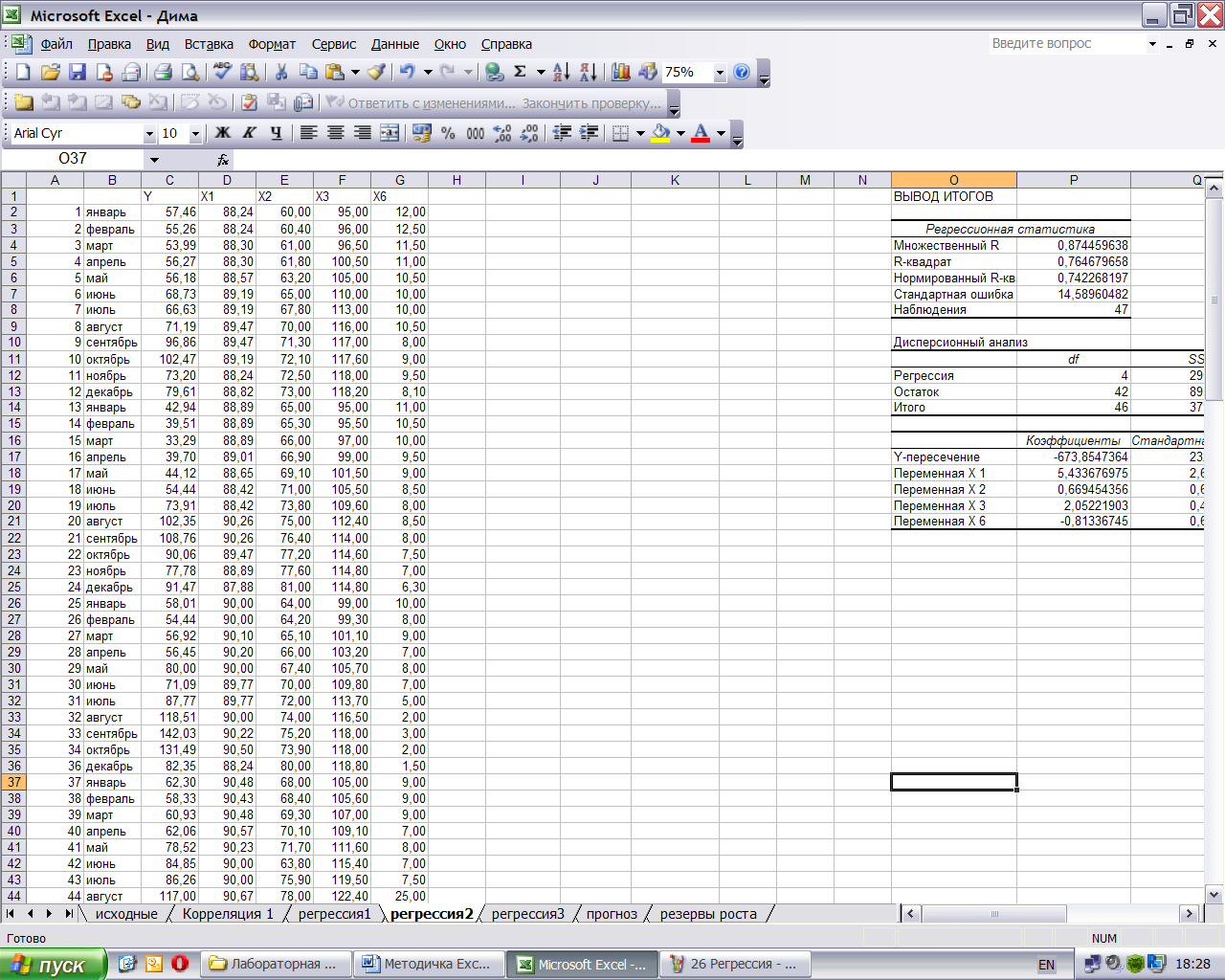
Проведите проверку отклонения фактических значений зависимой переменной Y от прогноза по регрессии как было показано выше (закладка Регрессия 1).

В указанном примере отклонение фактических значений зависимой переменной Y от прогноза по регрессии не превышает тройное среднеквадратическое отклонение. Поэтому переходим к окончательно проверке (п. 5).

5. Окончательная проверка значимости всех факторов проводится в ходе многошагового регрессионного анализа, где проверяется значимость каждого фактора в отдельности при одновременном совершенствовании каждого коэффициента регрессии, путем вычисления отношения:

,

где ak – коэффициент множественной регрессии k-го фактора;

- среднеквадратическое отклонение k-го фактора.

Среднеквадратическое отклонение каждого факторного признака множественной регрессии рассчитывается по формуле:

,

где x - значение факторного признака в соответствии с исходными данными;

- среднеарифметическое значение факторного признака.

Рассчитайте средние значения для факторных признаков по формуле (Лист Регрессия 1). Скопируйте данную формулу для остальных признаков.

Рассчитайте отклонения значения факторного признака в соответствии с исходными данными от среднеарифметического значения факторного признака. При вводе формулы среднее значение необходимо зафиксировать (нажать F4). Скопируйте формулу для всех наблюдений и факторных признаков.

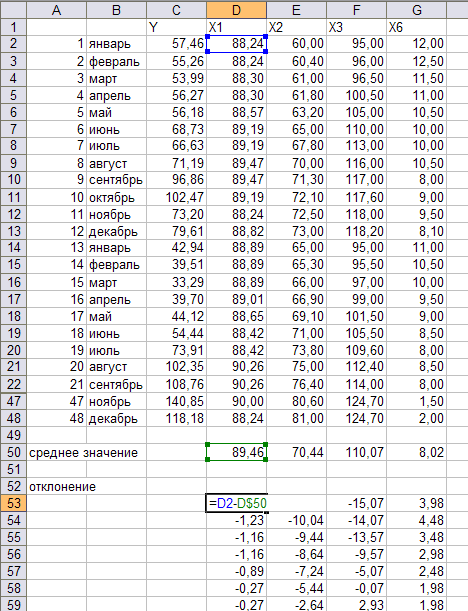
Ниже дополните таблицу таблицей отклонений в квадрате. Скопируйте формулу для всех наблюдений и факторных признаков.

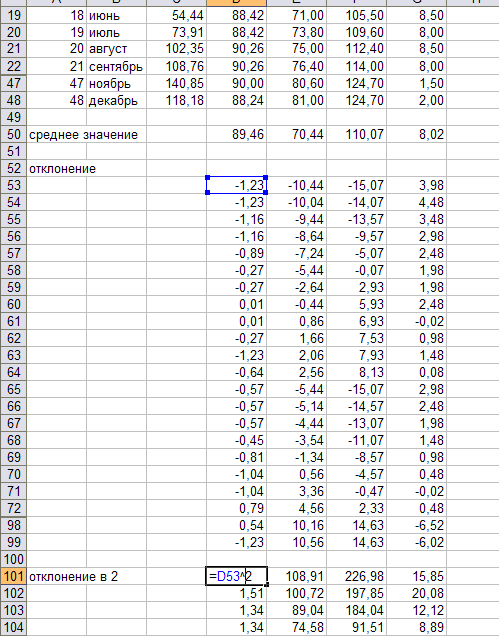
Рассчитайте сумму отклонений.

Рассчитайте среднеквадратическое отклонение k-го фактора. Скопируйте формулу для остальных факторов.

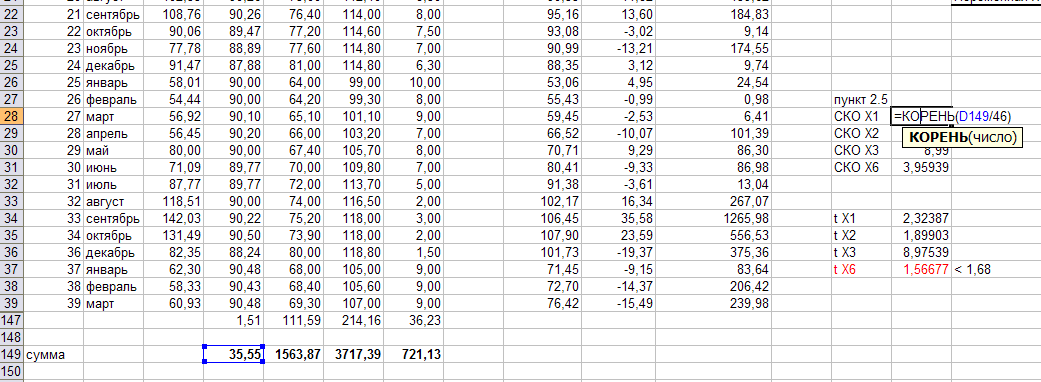
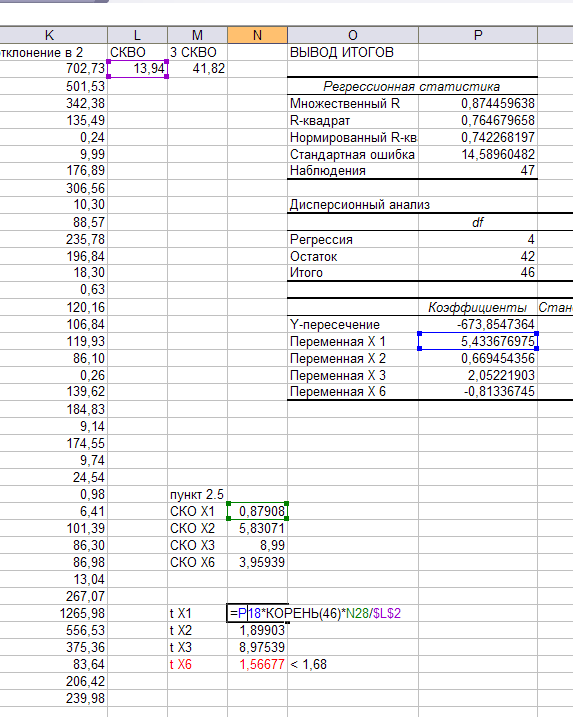
Рассчитайте значение t для каждого фактора по формуле:

Значение рассчитывается для всех факторов, входящих в состав уравнения множественной регрессии, за исключением тех факторов, которые были исключены из уравнения регрессии на предыдущих этапах работы по разным причинам:

• если отношение меньше табличного tα,ν, найденного по таблице t-распределения Стьюдента (Приложение №4) с α = 0,05 и ν = n-m-1 (n – число наблюдений, m - число объясняющих переменных), то с вероятностью 95% рассматриваемый факторный признак является в уравнении регрессии незначимым с n-m-1 степенями свободы;

• если отношение меньше табличного одновременно для нескольких факторов, то незначимые факторы исключаются из уравнения множественной регрессии поочередно, начиная с того факторного признака у которого отношениеминимальное. После исключения каждого факторного признака заново необходимо построить регрессию, поскольку ранее незначимые факторы могут стать значимыми после исключения одного из них;

• процесс исключения повторяется до тех пор, пока для всех факторных признаков будет выполняться неравенство ≥ tα,ν, что свидетельствует о том, что все факторы значимы.

В представленном примере значение t фактора Х6 меньше табличного, в связи с чем фактор Х6 исключается:

Исходные данные копируются на новый лист Регрессия 3

при этом столбец Х6 удаляется.

Проводится проверка как показано выше в данном пункте с вычислением значений .

В данном примере факторы Х1, Х2, Х3 прошли проверку.

6. Окончательная оценка значимости уравнения регрессии в целом производится с учетом статистики F- распределения Фишера:

,

где B – коэффициент детерминации,

n – количество наблюдений,

m – количество учитываемых объясняющих переменных.

Коэффициент детерминации рассчитывается по формуле:

Расчет значения В производится на листе Регрессия 3 аналогично расчету среднеквадратичного отклонения в пункте 2.5 по формуле:

F-распределение Фишера рассчитывается на том же листе по формуле:

Полученное значение F сравнивается с табличным значением F-распределения Фишера (Приложение №4). Если F≥Fα, то с вероятностью 95 % связь по уравнению регрессии является статистически значимой и нулевая гипотеза отвергается.

При получении статистически значимого уравнения регрессии определяются прогнозируемые значения факторных признаков, представленных в экономико-статистической модели, выявляются резервы роста производительности труда работников организации и их влияние на снижение затрат на производство СМР.