
- •Содержание
- •1. Функция. Основные определения. Последовательность. Предел последовательности
- •2. Предел функции непрерывного аргумента
- •3. Вычисление пределов функций. Основные приёмы
- •4. Замечательные пределы
- •5. Применение эквивалентных бесконечно малых к нахождению пределов функции. Сравнение бесконечно малых
- •6. Непрерывность функций. Точки разрывa.
- •Список литературы
- •Введение в математический анализ. Пределы
- •443086 Самара, Московское шоссе,34.
- •443086 Самара, Московское шоссе,34.
3. Вычисление пределов функций. Основные приёмы
Основные теоремы о пределах.
Теорема 1. Предел алгебраической суммы двух, трех и вообще определенного числа переменных равен алгебраической сумме пределов этих переменных:
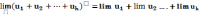
Теорема 2. Предел произведение двух и трех и вообще определенного числа переменных равен произведению пределов этих переменных.

Следствие: Постоянный множитель можно выносить за знак предела.
Теорема 3. Предел частного двух переменных равен частному пределов этих переменных, если предел знаменателя отличен от нуля:
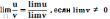
Теорема
4.
Если между соответствующими значениями
трех функций , , выполняются неравенства
≤ ≤ , при этом функции и при 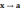
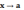 (или при
(или при
 )
стремятся к одному и тому же пределуb,
то при
)
стремятся к одному и тому же пределуb,
то при 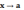
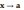 (или при
(или при
 )
стремится к тому же пределуb.
)
стремится к тому же пределуb.
Теорема
5.
Если при 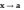
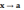 (или при
(или при
 )
функция у принимает неотрицательные
значенияy
≥ 0 и при этом стремится к пределу b
, то b
есть неотрицательное число (b
≥0).
)
функция у принимает неотрицательные
значенияy
≥ 0 и при этом стремится к пределу b
, то b
есть неотрицательное число (b
≥0).
Теорема
6.
Если между соответствующими значениями
двух функций и , стремящихся к пределам
при 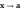
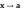 (или при
(или при
 ),
выполняется неравенство ≥, то имеет
место
),
выполняется неравенство ≥, то имеет
место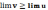
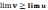 .
.
Теорема 7. Если переменная величина возрастает, т.е. всякое ее последующее значение больше предыдущего, и если она ограничена, т.е. <M, то эта переменная величина имеет предел
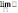
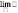
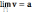
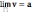 ,
где
,
где
 M
.
M
.
Пример
1.
Найти
предел
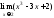 , применяя теоремы о пределах
, применяя теоремы о пределах
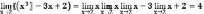
Пример
2.
Найти
предел
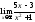
Чтобы
раскрыть неопределенность
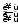 следует числитель и знаменатель поделить
почленно на переменную в высшей степени
(высшего порядка), стоящую в знаменателе.
следует числитель и знаменатель поделить
почленно на переменную в высшей степени
(высшего порядка), стоящую в знаменателе.
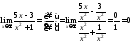
Пример
3.
Найти
предел
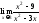
Чтобы
раскрыть неопределенность
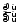 - при случаех→а
отношения двух многочленов, следует в
числителе и знаменателе дроби выделить
общий множитель вида (х -
а) и
на него сократить, т.к. под знаком предела
х
→
а,
но
никогда его не достигает.
- при случаех→а
отношения двух многочленов, следует в
числителе и знаменателе дроби выделить
общий множитель вида (х -
а) и
на него сократить, т.к. под знаком предела
х
→
а,
но
никогда его не достигает.
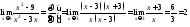 .
.
Пример
4.
Найти предел
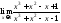 .
.
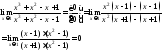
Пример
5.
Найти
предел
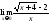 .
.
Чтобы
раскрыть неопределенность
 при х → а в случае отношения иррациональных
функций, следует начать с умножения на
выражение, сопряженное данному
иррациональному, с целью последующего
выделения общего множителя (х -а)
и
сокращения,
при х → а в случае отношения иррациональных
функций, следует начать с умножения на
выражение, сопряженное данному
иррациональному, с целью последующего
выделения общего множителя (х -а)
и
сокращения,
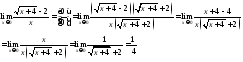
Пример
6.
Найти
предел
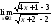 .
.
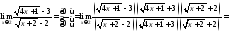
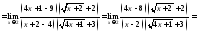
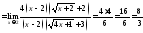
Пример
7.
Найти
предел
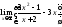 .
.
Чтобы
разрешить неопределенность
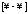 в
данном случае, следует привести выражение
к общему знаменателю.
в
данном случае, следует привести выражение
к общему знаменателю.
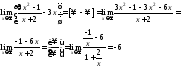
Пример
8.
Найти предел
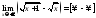
Чтобы
разрешить неопределенность
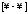 в данном случае, следует домножить и
разделить на сопряженное выражение.
в данном случае, следует домножить и
разделить на сопряженное выражение.
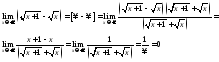
Задания для самостоятельной работы
Найти пределы:
1)
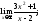 2)
2)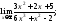 3)
3)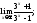
4)
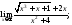 5)
5)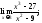
6)
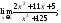 7)
7)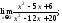
8)
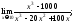 9)
9)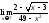 ;
;
10)
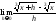 ;
11)
;
11)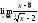 ;
;
12)
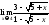 ;
13)
;
13)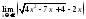 ;
;
14)
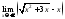 ;
15)
;
15)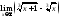
4. Замечательные пределы
Первый замечательный предел
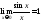
Пример
1.
Найти
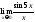
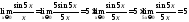 .
.
Пример
2.
Найти
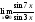
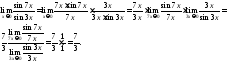
Пример
3.
Найти

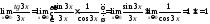
Пример
4.
Найти
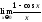
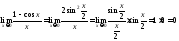
Второй замечательный предел.
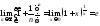 =
=
 .
.
Пример
5.
Найти
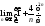 .
.
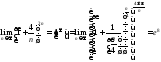
Пример
6. Найти
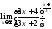 .
.
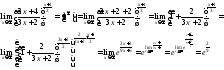
Пример
7.
Найти
 .
.
Если
 и
и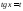 ,
то
,
то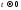 ,
тогда можно переписать
,
тогда можно переписать
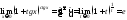
Пример
8.
Найти
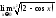 .
.
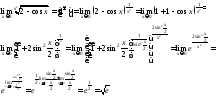
Пример
9.
Найти
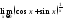 .
.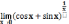
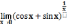
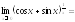
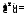
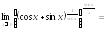


Задания для самостоятельной работы.
Найти:
1)
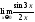 ;
2)
;
2)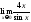 ;
3)
;
3)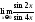 ;
;
4)
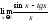 ;
5)
;
5)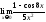 ;
6)
;
6)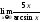 ;
;
7)
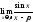 ;
8)
;
8)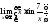 ;
9)
;
9)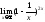 ;
;
10)
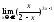 ;
11)
;
11)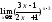 ;
12)
;
12)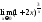 ;
;
13)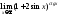 ;
14)
;
14)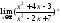 .
.
