
geokniga-ershovaovbakulinalpmineralogiyaipetrobookfiorg
.pdf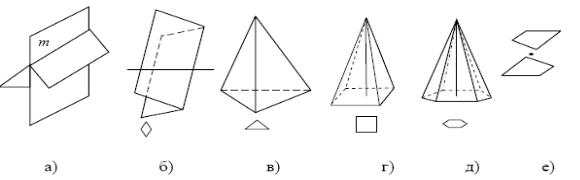
Инверсионная ось симметрии (инверсионно-поворотная, Li) – прямая линия, при повороте вокруг которой на 3600 с соответствующим переносом-отражением (инверсией) части фигуры через центр кристалла происходит его повторениесовмещение целое число раз. В кристаллах существуют инверсионные оси четвёртого и шестого порядков (Li4, Li6). Эти оси соответствуют: оси четвёртого порядка – осям симметрии второго порядка, а инверсионные оси симметрии шестого порядка
– осям симметрии третьего порядка. Порядок инверсионной оси симметрии определяется так же, как и порядок обычной оси симметрии, но он суммируется из количества обычных и отражённых совмещений.
Для определения инверсионной оси фигура поворачивается вокруг оси на 60 или 900, и все элементы её (рёбра, вершины, грани) проецируются через центр на противоположную сторону, то есть на 1800 в вертикальной плоскости. Если при этом все элементы нижней части фигуры отразятся через центр в её верхней части, в фигуре присутствует инверсионная ось.
Оси симметрии отсутствуют только в триклинной сингонии и планальном виде симметрии моноклинной сингонии, то есть только три формулы из 32 существующих не имеют осей симметрии.
Необходимо помнить следующее:
1.L6 и Li6 могут присутствовать в кристаллах в единственном числе;
2.L4 и Li4 могут быть или в единственном числе или в количестве трёх;
3.L3 могут быть или в единственном числе или в количестве четырёх;
4.L2 могут быть или в единственном числе или в количестве 2-х, 3-х, 4-х,
или 6; Перечень всех элементов симметрии кристалла (рис. 10), записанный в виде
их символов, называется формулой симметрии или видом симметрии.
Рис. 10. Повторение грани кристалла элементами симметрии:
а– плоскостью (m); б – двойной осью; в – тройной осью; г – четверной осью;
д– шестерной осью; е – центром инверсии
Строгий математический анализ (Гессель, 1830, Гадолин, 1867) показал, что существует всего 32 формулы симметрии. Это все возможные для кристаллов комбинации элементов симметрии.
11
В зависимости от наличия тех или иных элементов симметрии или их сочетания выделяются следующие виды симметрии:

 Примитивный – элементы симметрии в кристалле либо отсутствуют, либо кристалл характеризуется только наличием осей симметрии.
Примитивный – элементы симметрии в кристалле либо отсутствуют, либо кристалл характеризуется только наличием осей симметрии.


 Центральный – характеризуется обязательным присутствием центра симметрии и нескольких других элементов симметрии.
Центральный – характеризуется обязательным присутствием центра симметрии и нескольких других элементов симметрии.

 Аксиальный – характеризуется присутствием только осей симметрии разных порядков.
Аксиальный – характеризуется присутствием только осей симметрии разных порядков.

 Планальный – характеризуется обязательным присутствием плоскостей симметрии и отсутствием центра симметрии.
Планальный – характеризуется обязательным присутствием плоскостей симметрии и отсутствием центра симметрии.

 Планаксиальный – характерно присутстием всех элементов симметрии (оси, плоскости, центр) с максимальным количеством плоскостей и осей симметрии.
Планаксиальный – характерно присутстием всех элементов симметрии (оси, плоскости, центр) с максимальным количеством плоскостей и осей симметрии.

 Инверсионно-примитивный – характеризуется присутствием инверсионноповоротных осей симметрии в единичном количестве и отсутствием других элементов симметрии.
Инверсионно-примитивный – характеризуется присутствием инверсионноповоротных осей симметрии в единичном количестве и отсутствием других элементов симметрии.

 Инверсионно-планальный – характеризуется присутствием наряду с инвер- сионно-поворотными осями симметрии обычных осей симметрии второго порядка и плоскостей симметрии.
Инверсионно-планальный – характеризуется присутствием наряду с инвер- сионно-поворотными осями симметрии обычных осей симметрии второго порядка и плоскостей симметрии.
32 вида симметрии объединяются в сингонии. Сингония – группа видов симметрии, обладающая сходными элементами симметрии и имеющая одинаковое расположение кристаллографических осей. Название "сингония" происходит от греческого " син" – "сходно" и "гон" – "угол". Всего различают семь сингоний (рис. 11), которые объединены в три категории (табл. 1):
9Низшая категория объединяет триклинную, моноклинную и ромбическую сингонии. В кристаллах этих сингоний нет осей симметрии выше второго порядка.
9Средняя категория объединяет тригональную, тетрагональную и гексагональную сингонии. Кристаллы этих сингоний имеют только одну ось симметрии высшего порядка (L3, L4, L6).
9Высшая категория – кубическая сингония – объединяет кристаллы, которые обязательно имеют 4L3. Все направления симметрично-равные.
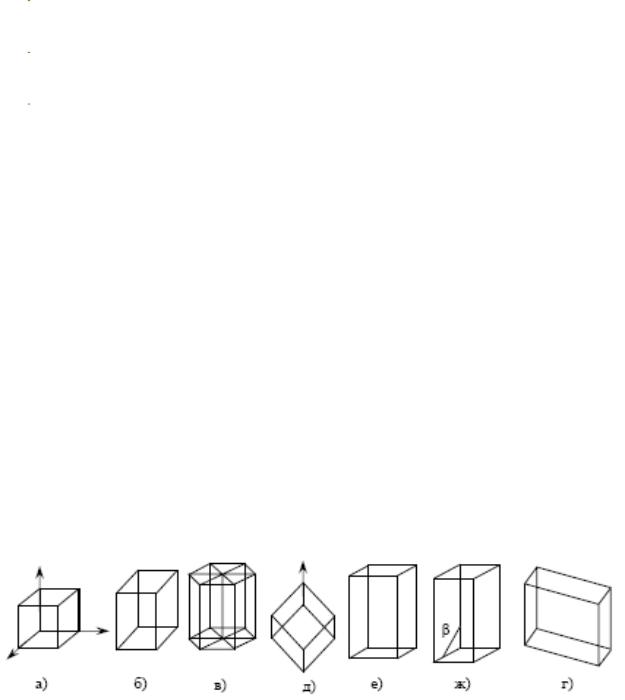
а – кубическая, б – тетрагональная, в – гексагональная и тригональная, г – триклинная, д – ромбоэдрическая, е – ромбическая, ж – моноклинная
Рис. 11. Формы примитивных ячеек семи сингоний
12
Таблица 1 – Характерные элементы симметрии
Категория |
Сингония |
Характерные элементы симметрии |
Низшая |
Триклинная |
Элементы симметрии отсутствуют или есть |
|
|
только один центр симметрии |
|
Моноклинная |
Одна ось симметрии второго порядка (L2) и од- |
|
|
на плоскость симметрии |
|
Ромбическая |
Число осей симметрии второго порядка (L2) и |
|
|
плоскостей симметрии равно трем |
Средняя |
Тригональная |
Одна ось симметрии третьего порядка (L3) |
|
Тетрагональная |
Одна ось симметрии четвертого порядка (L4) |
|
Гексагональная |
Одна ось симметрии шестого порядка (L6) |
Высшая |
Кубическая |
Четыре оси симметрии третьего порядка (4L3) |
Необходимо знать следующие правила:
1.В кристаллах низшей категории симметрии нет осей симметрии выше второго порядка L2. Это наименее симметричные кристаллы с ярко выраженной анизотропией свойств.
2.В кристаллах средней категории симметрии появляется одна главная ось, порядок которой выше второго L3, L4, L6. У этих кристаллов анизотропия физических свойств гораздо сильнее, чем у кристаллов высшей категории.
3.Кристаллы высшей категории имеют несколько осей порядка выше, чем 2, в частности четыре оси L3, расположенные как пространственные диагонали куба. Помимо 4L3 в кристаллах кубической сингонии всегда имеются либо 3L4, либо 3L2. Это высокосимметричные кристаллы. Анизотропия свойств в кристаллах высшей категории выражена слабее всего.
Совокупность элементов симметрии кристалла образует его кристаллографическую формулу симметрии, в которой на первом месте записываются оси симметрии, затем плоскости и в конце – центр симметрии. Никаких знаков препинания между ними не ставится. Если многогранник не обладает никакими элементами симметрии, то его формула будет L1. Оси симметрии записываются последовательно от осей высшего порядка к осям низшего порядка.
Например, куб (гексаэдр) обладает тремя осями 4-го порядка, четырьмя осями 3- го порядка, шестью осями 2-го порядка, девятью плоскостями симметрии и центром симметрии, следовательно, его формула симметрии будет записана как 3L44L36L29PC.
Аформулой симметрии кристалла в виде кирпичика или спичечной коробки будет 3L23PC. Нередко совершенно разные на вид многогранники имеют одинаковые элементы симметрии и, соответственно, одинаковую формулу симметрии.
Втабл. 2 приводится химический состав и сингонии минералов шкалы твердости Мооса.
13
Таблица2 – ХимическийсостависингонииминераловшкалытвердостиМооса
Твердость |
|
|
|
Формула |
|
|||
по шкале |
Минерал |
химическая |
|
симметрии; |
Спайность |
|||
Мооса |
|
|
сингония |
|
||||
|
|
|
|
|
|
|||
1 |
Тальк |
Mg3[Si4O10](OH)2 |
L2PC |
в.с. |
||||
моноклинная |
||||||||
|
|
|
|
|
|
|
||
2 |
Гипс |
Ca[SO ]·2H O |
|
- |
в.с. |
|||
|
моноклинная |
|||||||
|
|
|
4 |
2 |
|
|
||
3 |
Кальцит |
|
Ca[CO3] |
|
|
L33L23PC |
с. |
|
|
|
|
тригональная |
|||||
|
|
|
|
|
|
|
||
4 |
Флюорит |
|
CaF2 |
|
|
3L44L36L29PC |
с. |
|
|
|
|
кубическая |
|||||
|
|
|
|
|
|
|
||
5 |
Апатит |
Ca5[PO4]3(F, Cl) |
|
L6PC |
н.с. |
|||
|
гексагональная |
|||||||
|
|
|
|
|
|
|
||
6 |
Ортоклаз |
K[Al Si3O8] |
|
L2PC |
в.с. |
|||
|
моноклинная |
|||||||
|
|
|
|
|
|
|
||
7 |
Кварц |
|
SiO2 |
|
|
Li6C |
в.н.-с. |
|
|
|
|
тригональная |
|||||
|
|
|
|
|
|
|
||
8 |
Топаз |
Al [SiO ](F, OH) |
|
3L2; 3L23PC |
с. |
|||
2 |
ромбическая |
|||||||
|
|
2 |
4 |
|
|
|||
9 |
Корунд |
|
Al2O3 |
|
|
L3 |
- |
|
|
|
|
тригональная |
|||||
|
|
|
|
|
|
|
||
10 |
Алмаз |
|
C |
|
|
3L44L36L29PC |
ср. |
|
|
|
|
|
|
|
кубическая |
|
|
Примечание: Буквенные значения видов спайности: в.с. - весьма совершенная; с. -совершенная; ср. - средняя; н.-с. – несовершенная; в.н.-с. – весьма несовершенная; - отсутствие спайности.
Контрольные вопросы
1.Какие преобразования необходимо совершить с кристаллом, чтобы доказать его симметричность?
2.Какие элементы симметрии кристалла вы знаете?
3.Что называется плоскостью симметрии?
4.Каким символом обозначают плоскость симметрии?
5.Какая фигура имеет 9 плоскостей симметрии?
6.Что называется центром симметрии?
7.Какие оси симметрии возможны в кристаллах?
8.Что такое инверсионные оси симметрии? Как определить их порядок?
9.Что называется видом симметрии? Какие виды симметрии вы знаете?
10.Что такое формула симметрии?
11.Сколько существует сингоний и категорий в кристаллографии?
12.Какая сингония относится к высшей категории?
13.Какие виды симметрии содержат центр инверсии?
14.Какие виды симметрии содержат центр инверсии, инверсионные оси,
только оси симметрии?
14

3. Простые формы кристаллов низшей категории
Изучение кристаллов, их элементов симметрии показывает, что совершенно разные по внешнему облику кристаллы могут иметь одинаковые формулы симметрии. Следовательно, одного определения элементов симметрии недостаточно, чтобы определить и охарактеризовать конкретный кристалл. Объясняется это тем, что каждый кристалл имеет характерную форму, представляющую собой сочетание разных по форме и размеру граней.
Простой формой называется сочетание одинаковых по размеру и форме граней, связанных друг с другом элементами симметрии. Каждый кристалл может представлять собой простую форму, если он состоит из одинаковых по форме и размеру граней. Он может быть также комбинацией простых форм, если образован разными по форме и размерам гранями. Следовательно, в кристалле столько простых форм, сколько типов граней он содержит. Для определения простой формы в кристалле надо взять любую грань, сосчитать ее количество и уяснить ее положение.
Название простых форм, как правило, происходит от греческих слов: гония – угол; пинакое – доска; эдра – грань; клинос – наклонный; скаленос – косой, неровный; трапезос – четырехугольник; морфо – форма, образ, вид; 1 – моно, 2 – ди, 3 – три, 4 – тетра, 5 – пента, 6 – гекса, 7 – гепта, 8 – окта, 10 – дека, 12 – додека.
В связи с особенностями строения кристаллов различных видов симметрии для каждого из них характерны и возможны только определённые простые формы. Число типов простых форм равняется 47: 7 – в низшей, 25 – в средней и 15 в высшей категориях.
Названия большей части простых форм низшей и средней категорий содержат два признака: первый указывает на форму основания, второй – на общее название фигуры (призма, пирамида, дипирамида). Основанием таких фигур может служить один из правильных многоугольников, показанных на рис. 12.
а– ромб, б – тригон (равносторонний треугольник), в – дитригон (удвоенный равносторонний треугольник), г – тетрагон (квадрат), д – дитетрагон (удвоенный квадрат),
е– гексагон (правильный шестиугольник), ж – дигексагон (удвоенный шестиугольник)
Рис. 12. Формы оснований призм, пирамид, дипирамид
Низшую категорию характеризуют следующие простые формы: моноэдр, пинакоид, диэдр, тетраэдр, призма ромбическая, пирамида ромбическая, дипирамида ромбическая (рис. 13).
15

а – моноэдр, б – пинакоид, в – диэдр, г – ромбическая пирамида, д – ромбическая призма, е – ромбический тетраэдр, ж – ромбическая дипирамида
Рис. 13. Простые формы низшей категории
Моноэдр – одиночная, неповторяемая грань в кристалле. Моноэдром является, например, основание пирамиды.
Пинакоид – простая форма, образованная двумя равными параллельными гранями. Ориентировка и положение граней кроме параллельности не имеют значения.
Диэдр – простая форма, образованная двумя равными гранями, расположенными под углом друг к другу.
Тетраэдр – простая форма, образованная четырьмя одинаковыми по форме и размерам гранями. Каждая грань имеет форму разностороннего треугольника.
Ромбическая призма – простая форма, которая состоит из четырех равных, попарно параллельных граней, которые в сечении образуют ромб.
Ромбическая пирамида – простая форма состоит из четырех равных пересекающихся граней; в сечении также – ромб.
Ромбический тетраэдр – простая форма, четыре грани которой имеют форму косоугольных треугольников и замыкают пространство.
Ромбическая дипирамида – две ромбические пирамиды, сложенные основаниями. Форма имеет восемь равных граней, дающих в поперечном сечении ромб.
4. Простые формы кристаллов средней категории
Средняя категория часть простых форм наследует из низшей категории, к которым относятся: моноэдр, пинакоид, тетраэдр (в отличие от ромбического тетраэдра тетрагональный имеет форму грани в виде равнобедренного треугольника), призма, пирамида и дипирамида (рис. 14). Последние три простые формы в соответствии с типом сингонии имеют треугольную, квадратную или шестиугольную форму сечения. В средней категории они могут быть тригональными, тетрагональными и гексагональными.
В средней категории полностью исчезает |
1 – ромбическая; 2 |
– тригональная; |
|
3 – тетрагональная; |
4 – гексагональная |
||
такая простая форма, как диэдр. Из новых форм |
|||
Рис. 14. Внешний вид призм |
|||
в средней категории появляются: ромбоэдр, трапецоэдр, скаленоэдр.
16
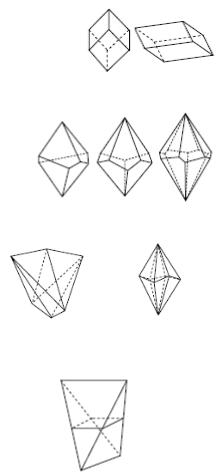
Ромбоэдр (рис. 15) – простая форма, состоящая из 6 рав- |
|
ных граней, три из которых располагаются не строго под (или |
|
над) другими тремя, а повёрнуты относительно друг друга на |
|
некоторый угол. Форма граней ромбоэдра – ромбическая. |
Рис. 15. Ромбоэдры |
Трапецоэдр (рис. 16) устроен аналогично ромбоэдру, но форма грани у него представляет собой трапецию. Эти фигуры отличаются от соответствующих дипирамид тем, что нижняя половина их находится не точно под верхней, а
смещена относительно нее на некоторый угол. |
Рис. 16. Трапециоиды |
|
|
Скаленоэдр (рис. 17) – простая форма, пред- |
|
ставляющая собой тетрагональный тетраэдр с раз- |
|
двоенной гранью или тригональный ромбоэдр с раз- |
|
двоенной гранью. |
Рис. 17. Тетрагональный |
|
и гексагональный скаленоэдры |
Тетрагональный тетраэдр (рис. 18) пред- |
|
ставляет собой четыре равные грани в виде равно- |
|
бедренных треугольников. |
|
|
Рис. 18. Тетрагональный |
|
тетраэдр |
5. Простые формы кристаллов высшей категории
Высшая категория имеет только одну простую форму, сходную с формами низшей и средней категории – тетраэдр. Но при этом тетраэдр кубической сингонии отличается от тетрагонального и ромбического тетраэдра тем, что его грани являются равносторонними треугольниками, тогда как у тетрагонального тетраэдра они являются равнобедренными, а у ромбического – произвольными треугольниками с тремя неравными ребрами.
Все остальные простые формы кубической сингонии новые. К ним относятся: гексаэдр, октаэдр, додекаэдр и производные от них формы (рис. 19).
Гексаэдр представляет собой правильный шестигранник (куб) с квадратной формой грани.
Октаэдр – это простая форма в виде правильного восьмигранника. Додекаэдр – правильный двенадцатигранник. В зависимости от формы грани
могут быть следующие простые формы этого типа: ромбододекаэдры – форма грани в виде ромба; пентагондодекаэдры с формой грани в виде пятиугольника. Правильный двадцатичетырёхгранник называется дидодекаэдром.
17

Рис. 19. Простые формы кубической сингонии
Куб (гексаэдр) (а), тетрагексаэдр (б), ромбододекаэдр (в), пентагондодекаэдр (г), дидодекаэдр (д)
При четырёх основных простых формах высшей категории (тетраэдр, гексаэдр, октаэдр и додекаэдр) существуют комбинированные простые формы. Названия таких форм кубической сингонии даны по следующему принципу: первая часть слова (тригон, тетрагон, пентагон) характеризует очертание грани данной формы (тригон = три + гон = треугольник), вторая часть слова (тритетраэдр - триоктаэдр) указывает: а) от какой простой формы данная форма является производной; б) сколько граней данной формы расположено на каждой грани простой формы; в) чему равно число граней данной формы.
Примеры названий комбинированных простых форм:
1.Кристалл представляет собой тетраэдр, у которого каждая из четырёх граней состоит из трёх маленьких треугольных граней. Такая форма будет иметь на-
звание тригон-три-тетраэдр.
2.Кристалл представляет собой октаэдр, каждая из восьми граней которого составлена из трёх малых четырёхугольных граней. Такая форма имеет назва-
ние тетрагрн-три-октаэдр.
Если взять за исходные простые формы тетраэдр и октаэдр, то можно получить ряд производных простых форм (рис. 20).
|
|
|
|
Форма граней |
|
|
|
|
|
|
|
|
|
форма |
Октаэдр |
|
|
|
|
|
|
Тетраэдр |
Тригонтритетраэдр |
Тетрагонтритетраэдр |
Пентагонтритетраэдр |
Гексатетраэдр |
|
Исходная |
|
|||||
Тетраэдр |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Октаэдр |
Тригонтриоктаэдр |
Тетрагонтриоктаэдр |
Пентагонтриоктаэдр |
Гексаоктаэдр |
Рис. 20. Простые формы кубической сингонии, образованные от тетраэдра и октаэдра
В верхней строке показаны формы граней. Первой изображена грань правильного (кубического) тетраэдра – равносторонний треугольник. Если вместо одной
18
грани появляются три, то фигура называется тритетраэдр, если шесть – гексатетраэдр. Так как тритетраэдров может быть несколько, то перед названием указывается форма каждой из получающихся граней. Грани тритетраэдров могут быть треугольные, четырехугольные и пятиугольные, соответственные фигуры, имеющие такие грани, получают название тригон-тритетраэдр, тетрагон-тритетраэдр и пентагонтритетраэдр.
Те же самые по форме грани могут быть и у октаэдров (нижняя строка). Их названия получаются таким же образом, как и для тетраэдров.
Соответственно получим следующие 5 простых форм кубической сингонии: октаэдр, тригон-триоктаэдр, тетрагон-триоктаэдр, пентагон-триоктаэдр и гексаоктаэдр.
Общее число граней у всех простых форм легко может быть высчитано, если учитывать их название.
Тетраэдр и октаэдр имеют соответственно 4 и 8 граней. Все тритетраэдры будут иметь по 12 граней, а триоктаэдры – по 24 . Гексатетраэдр также имеет 24 грани, а гексаоктаэдр – 48. Это максимальное число граней, которое может иметь простая форма.
Для определения простой формы кристаллов кубической сингонии следует сориентировать кристалл таким образом, чтобы одинаковые группы граней можно было свести к одной из базовых простых форм (тетраэдр, октаэдр, додекаэдр). После этого легко определить название комбинированной формы.
6. Комбинированные формы кристаллов
При росте кристаллов чаще образуются не простые формы, а их сочетания, комбинации. Комбинированной формой кристалла называют форму, состоящую из двух или более простых форм, соединенных в единый многогранник посредством элементов симметрии. Однако простые формы кристаллов не могут комбинироваться как угодно. На этот счет имеется жесткое правило: комбинируются между собой простые формы, принадлежащие лишь одной и той же сингонии. Исключением являются простые формы двух родственных сингоний – тригональной и гексагональ-
ной, которые могут образовывать совместные комбинации.
Примером комбинации может служить шестигранная пирамида. Шесть одинаковых треугольных граней представляют одну простую форму. Все они могут быть получены вращением одной грани вокруг L6. Резко отличается от них грань основания, которая принадлежит другой простой форме. В результате получается комбинация, состоящая из двух простых форм.
19
Комбинаций возможно бесконечное множество, в Приложении 2 указаны некоторые из них.
Контрольные вопросы:
1. Что такое простая форма?
3.Какие вам известны призмы, пирамиды, дипирамиды?
4.Какие вы знаете трапецоэдры? Каковы их характерные признаки?
5.Перечислите простые формы, содержащие: а) одну; б) две; в) три; г) четыре; д) шесть граней?
6.Назовите двенадцатигранники высшей категории.
7.Перечислите все простые формы, имеющие а) 12; б) 24; в) 48 граней.
8.Чем отличаются тригональный трапецоэдр, тригональная дипирамида и ромбоэдр?
9.Чем отличаются ромбический, тетрагональный и кубический тетраэдр?
10.Сопоставьте простые формы: а) пентагондодекаэдр и ромбододекаэдр; б) тетрагонтриоктаэдр и дидодекаэдр; в) ромбододекаэдр и ромбоэдр.
11.Что такое комбинация простых форм?
12.Как определить число простых форм, образовавших комбинацию?
13.Перечислите основные правила распределения простых форм по категориям и сингониям.
14.Какое максимальное число граней может иметь простая форма?
15.Сколько всего возможно комбинированных форм?
20
