
- •1. Определение функции нескольких переменных. Основные понятия.
- •2. Область определения и область значений функции нескольких переменных. График функции нескольких переменных. (см1)
- •3. Предел и непрерывность функции нескольких переменных.
- •4. Дифференцируемость функции нескольких переменных, частные производные, полный дифференциал.
- •5. Экстремум функции двух переменных: необходимое и достаточное условия.
- •6. Неопределенный интеграл и его свойства.
- •7. Таблица интегралов.
- •8. Методы интегрирования неопределенного интеграла: непосредственное, подстановки, по частям, разложение дроби на простейшие, тригонометрических функций.
- •9. Определенный интеграл и его геометрический смысл
- •10. Свойства определенного интеграла
- •11. Формула ньютона-лейбница (основная формула интегрального исчисления (!) )
- •12. Методы интегрирования определенного интеграла
- •13) Геометрические приложения определенного интеграла
- •14. Несобственные интегралы первого рода
- •15. Несобственные интегралы второго рода
- •16. Дифференциальные уравнения. Основные понятия.
- •19. Линейные дифференциальные уравнения 1-го порядка и уравнение Бернулли.
- •27. Элементы комбинаторики: правила суммы и произведения.
- •28. Алгебра событий: сумма, произведение событий. Противоположные события. Примеры.
- •29. Теорема сложения вероятностей для несовместных событий.
- •30. Зависимые и независимые события. Условная вероятность.
- •31. Теорема умножения вероятностей для зависимых и независимых событий.
- •32. Теорема сложения вероятностей для совместных событий.
- •33. Формула полной вероятности и формулы Байеса.
- •34. Повторные независимые испытания: постановка задачи, формула Бернулли.
- •35. Локальная теорема Муавра-Лапласа: формулировка теоремы, приближенная формула.
- •40. Закон распределения и функция распределения дискретной случайной величины.
- •41. Свойства интегральной функции распределения.
- •47. Числовые характеристики непрерывных случайных величин.
- •52. Закон больших чисел: неравенство Чебышева.
- •53. Теорема Чебышева.
- •54. Теорема Бернулли.
- •55. Понятие о центральной предельной теореме Ляпунова.
- •56. Генеральная совокупность и выборка: основные определения и понятия.
- •57. Статистическое распределение. Полигон и гистограмма.
- •58. Точечные и интервальные статистические оценки и их свойства.
- •59. Доверительный интервал для оценки неизвестного математического ожидания нормального распределения генеральной совокупности при известном среднем квадратическом отклонении вычисляется по формуле
- •60. Корреляция и регрессия. Метод наименьших квадратов.
- •61. Проверка статистических гипотез. Основные понятия.
11. Формула ньютона-лейбница (основная формула интегрального исчисления (!) )
Если f(x) непрерывна на отрезке [a;b], и F(x) - некоторая первообразная функции f(x), То:
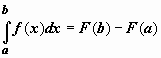
Формулу Ньютона-Лейбница обычно записывают так:

12. Методы интегрирования определенного интеграла
1) Метод замены переменной. Пусть функция x=φ(t) имеет производную во всех точках отрезка [α;β] и отображает этот отрезок на отрезке [a,b] таким образом, что a= φ(α) и b=φ(β). Тогда

2) Интегрирование по частям
Пусть функции u(x) и v(x) имеют производные во всех точках отрезка [a,b]. Тогда:
![]()
3) Метод непосредственного интегрирования. С помощью тождественных преобразований подынтегральной функции интеграл сводится к интегралу, к которому применимы основные правила интегрирования и возможно использование таблицы основных интегралов.
4) Интегрирование дробей. Элементарными дробями называются дроби следующих 4-ёх типов:
1)
 ;
2)
;
2)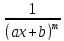 ;
3)
;
3) ; 4)
; 4) , гдеm,
n–натуральные
числа (m≥2,
n≥2,
b2-4ac<0)
, гдеm,
n–натуральные
числа (m≥2,
n≥2,
b2-4ac<0)
Дробь
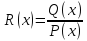 - правильная, если степень числителя
меньше степени знаменателя, в противном
случае дробь называется неправильной.
- правильная, если степень числителя
меньше степени знаменателя, в противном
случае дробь называется неправильной.
Если
 – правильная рациональная дробь,
знаменательP(x)
которой представлен в виде линейных и
квадратичных множителей P(x)=
– правильная рациональная дробь,
знаменательP(x)
которой представлен в виде линейных и
квадратичных множителей P(x)= ,
то эта дробь может быть разложена на
элементарные дроби по схеме:
,
то эта дробь может быть разложена на
элементарные дроби по схеме:
 =
= +…
+… +…+
+…+ +
+ +…+
+…+ +
+ +
+ +…+
+…+ ,где
A1…Ak,
B1
… Bp,
M1…Me,
N1…Nl
– некоторые
действительные числа. Коэффициенты Аi,
Bi,
Mi,
Ni
находят методом неопределенных
коэффициентов или методом частных
значений. Для этого необходимо привести
равенства к общему знаменателю, приравнять
коэффициенты при одинаковых степенях
x
в левой и правой частях полученного
тождества и решить систему линейных
уравнений относительно искомых
коэффициентов. Можно определить
коэффициент и другим способом, придавая
в полученном тождестве переменной х
произвольное числовое значение.
,где
A1…Ak,
B1
… Bp,
M1…Me,
N1…Nl
– некоторые
действительные числа. Коэффициенты Аi,
Bi,
Mi,
Ni
находят методом неопределенных
коэффициентов или методом частных
значений. Для этого необходимо привести
равенства к общему знаменателю, приравнять
коэффициенты при одинаковых степенях
x
в левой и правой частях полученного
тождества и решить систему линейных
уравнений относительно искомых
коэффициентов. Можно определить
коэффициент и другим способом, придавая
в полученном тождестве переменной х
произвольное числовое значение.
5)Интегрирование тригонометрических функций: универсальная тригонометрическая подстановка.
Интеграла вида
 ,
гдеR
– рациональная функция, приводятся к
интегралам от рациональных функций с
помощью универсальной
тригонометрической подстановки:
tg
,
гдеR
– рациональная функция, приводятся к
интегралам от рациональных функций с
помощью универсальной
тригонометрической подстановки:
tg =t
=t
В результате
подстановки: sinx= =
= cosx=
cosx= =
= x=2arctg(t)
dx=
x=2arctg(t)
dx=
Интегралы вида

1) Один из показателей m или n – нечетное положительное число.
Если n - нечетное положительное число, то подстановка sin x=t
Если m - нечетное положительное число, то подстановка cos x=t
2) Оба показателя степени m и n – четные положительные числа. Надо преобразовать подынтегральную функцию с помощью формул:
sinx*cosx=½sin(2x)


Интегралы вида
 ,
, ,
, .
Подынтегральную функцию преобразовываем
с помощью тригонометрических формул:
.
Подынтегральную функцию преобразовываем
с помощью тригонометрических формул:
![]()
![]()
![]()
13) Геометрические приложения определенного интеграла
а) Пусть f(x) положительна и непрерывна на [a;b]. Тогда площадь криволинейной трапеции, ограниченной сверху кривой y=f(x) выражается определенным интегралом: (выше оси Ox)


б) Пусть функция y=f(x) отрицательна и непрерывна на [a;b], т.е. кривая y=f(x) и криволинейная трапеция лежат под осью Ох. Тогда:


в) Общий случай, когда некоторые части кривой лежат над осью Ох, а другие – под осью Ох. Площадь криволинейной трапеции - алгебраическая сумма площадей тех частей фигуры, которые расположены над Ох, и тех ее частей, которые под Ох, причем первые входят в сумму с «+», а вторые – с «-».
Тогда:


г) Пусть фигура ограничена сверху и снизу кривыми y1=f1(x), y2=f2(x) и f1(x)≤f2(x), a≤x≥b, где f1(x), f2(x) – непрерывные функции. Тогда:
![]() f1(x),
f2(x)
– отрицательные значения
f1(x),
f2(x)
– отрицательные значения
Объем тела вращения:
y=f(x), f(x) – непрерывна на [a;b]. Если соответственно ей криволинейную трапецию вращать вокруг оси Ох, то получим тело вращения. Каждое сечение тела плоскостью х=const – это круг радиуса R=│y(x)│
Vx=π

Если криволинейную трапецию вращать вокруг оси Оy, то объем тела вращения по формуле:
Vy=π

