9. Определенный интеграл и его геометрический смысл

Геометрический смысл определенного интеграла:

Криволинейная трапеция – это фигура, ограниченная сверху кривой y=f(x), снизу – отрезком [a;b], слева – прямой х = а, справа – прямой х = b.

Определенный интеграл – площадь криволинейной трапеции

Достаточное условие существование определенного интеграла: если функция y=f(x) непрерывна на [a;b], то она интегрируема на этом отрезке.

Обязательная составляющая криволинейной трапеции – нижнее основание в виде [a;b] и верхняя часть в виде кривой y=f(x).

Пусть функция f(x) определена на [a;b]. Разобьем этот промежуток на n произвольных частей точками x₀, x₁, x₂,…x_n, полагая, что a=x₀<x₁<x₂<…<x_n-1<x_n=b

В каждом из полученных частичных промежутков [xi;xi+1], где i=0,1,2…выберем произвольную точку Ę_i (x_i≤Ę_i≥x_i+1)

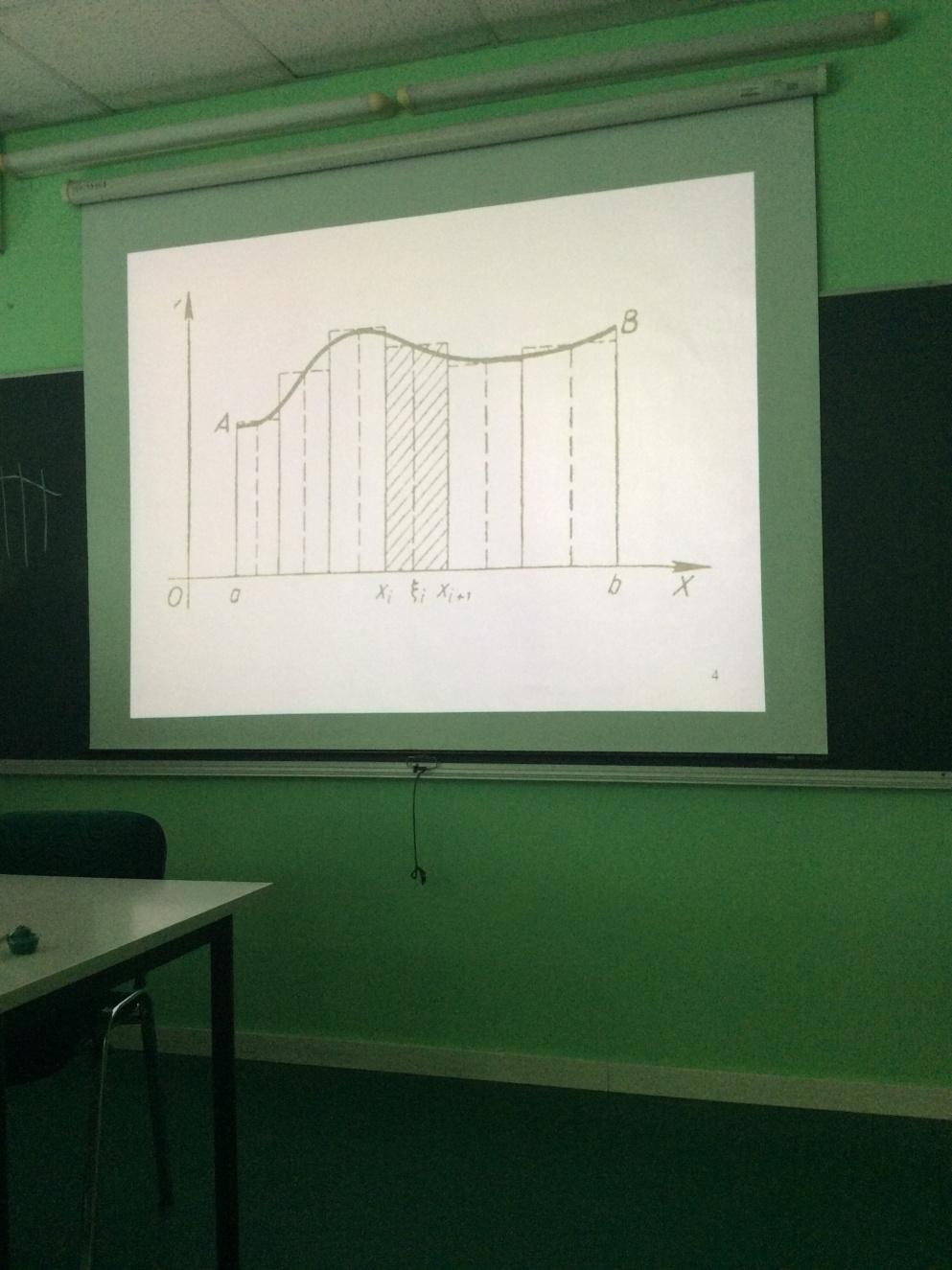
Вычислим значения функций f(Ę) и умножим его на разность x_i+1-x_i=Δ x_i. После этого составим сумму:

Если существует конечный предел интегральной суммы при λ→0, не зависящий ни от способа дробления промежутка [a;b] на части, ни от выбора точки Ę_i, то этот предел – определенный интеграл функции f(x)по промежутку [a;b]: I=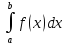

10. Свойства определенного интеграла

1) Если переставить пределы интегрирования, то изменится лишь знак:

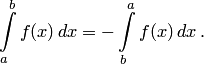
2) Каковы бы ни были а и b, всегда имеет место равенство:

3) Постоянный множитель А выносится за знак определенного интеграла:

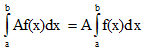
4) Определенной интеграл от алгебраической суммы конечного числа непрерывных функций равен такой же алгебраической сумме определенных интегралов от этих функций:

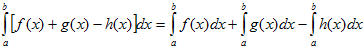
5) Если f(x) – неотрицательная на [a;b], функция и нижний предел меньше верхнего предела (a<b), то и сам интеграл – число неотрицательное, т.е.:

Замечание: если f(x) ≤0 на [a;b] и a<b, то 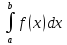≤0

Если f(x) ≥0 на [a;b] и a>b имеем ≤0

Если f(x) ≤0 на [a;b], то 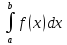≥0

6) Если a ≤ b, а f(x) и u·g(x) - две непрерывные функции, которые на [a, b] удовлетворяют условию f(x) ≤ g(x), то:

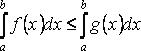, т.е. неравенство почленно интегрируется.

7) Если a ≤ b и f(x) непрерывна на [a, b], то:

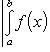
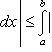
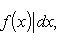, т.е. абсолютная величина интеграла не превосходит интеграла абсолютной величины подынтегральной функции.

8) Если m и M – наименьшее и наибольшее значения функции f(x) на отрезке [a;b], то:

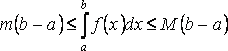
9) Теорема о среднем:

Если функция f(x) непрерывна на [a;b], то существует хотя бы одна точка С на этом отрезке, такая, что справедливо равенство:

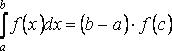
Замечание: формула справедлива также для a>b, кроме a<b

Если a>b, то:

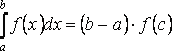, (b=<c=<a)

Отсюда

Геометрический смысл:

Если f(x) >=0 на отрезке [a;b], то интеграл левой части есть площадь криволинейной трапеции, ограниченной сверху кривой y=f(x), а правая часть – площадь прямоугольника с тем же основанием и h=f(c). Для площади криволинейной трапеции всегда есть равновеликий ей прямоугольник с тем же основанием и h, равной ординате этой кривой.

10) Определенный интеграл с одинаковыми пределами равен 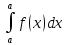0.

=0

Определенный интеграл как функция верхнего предела:

В отличие о неопределенного интеграла, определенный интеграл – это число, величина которого зависит только от пределов a и b. Если изменить верхний предел, то величина интеграла изменится.

Интеграл с переменным верхним пределом есть функция своего верхнего предела Ф(х):

Теорема: производная определенного интеграла от непрерывной функции по его верхнему пределу существует и равна подынтегральной функции в верхнем пределе.

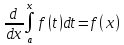
Если функция f(x) – непрерывна, то она имеет первообразную F(x), равную определенному интегралу.