1. Определение функции нескольких переменных. Основные понятия.

Если каждой паре независимых друг от друга чисел (х,у) из некоторого множества по какому-либо правилу ставится в соответствие одно значение переменной z, то она называется функцией двух переменных. z=f(x,y,)

Область определения функции z - совокупность пар (х,у), при которых функция z существует.

Множество значений (область значений) функции – все значения, которые принимает функция в ее области определения.

График функции двух переменных - множество точек P, координаты которых удовлетворяют уравнению z=f(x,y)

Окрестность точки M0 (х0;y0) радиуса r – совокупность всех точек (x,y), которые удовлетворяют условию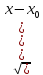<r

2. Область определения и область значений функции нескольких переменных. График функции нескольких переменных. (см1)

3. Предел и непрерывность функции нескольких переменных.

Число А называется пределом функции f(x,y) при стремлении точки М(х,у) к точке М₀(х₀,у_о), если для любого числа Е>0 найдётся такое число r>0, что для любой точки М(х,у), для которых верно условие ММ₀<r также верно условие

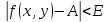
Записывают:

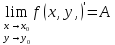
Пусть точка М₀(х₀,у₀) принадлежит области определения функции f(x,y). Тогда функция z=f(x,y) называется непрерывной в точке М₀(х₀,у₀), если 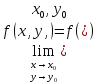, причём точка М(х,у) стремится к точке М₀(х₀,у₀) произвольным образом.

Если в какой-либо точке условие 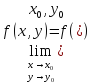не выполняется, то эта точка разрыва функции f(x,y). Это может быть в случаях:

1. Функция z=f(x,y) не определена в точке М₀(х₀,у_о)

2. Не существует предел в точке М₀(х₀,у_о),

3. Этот предел существует, но не равно f(х₀,у_о)

4. Дифференцируемость функции нескольких переменных, частные производные, полный дифференциал.

Функция называется дифференцируемой в данной точке, если ее полное приращение в этой точке может быть представлено в виде:, где А₁, А₂, …, А_m – некоторые не зависящие от ∆х₁, ∆х₂, …, ∆х_m числа, а α₁, α₂, …, α_m – бесконечно малые при 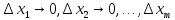функции, равные 0 при ∆х₁=∆х₂=…∆х_m=0.

Частная производная функции z=f(x,y) по х – предел отношения частного приращения функции по х к приращению Δх при Δх→0, если он существует и конечен: =

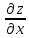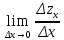
Частная производная функции z=f(x,y) по y- – предел отношения частного приращения функции по y к приращению Δy при Δy→0, если он существует и конечен:: =

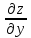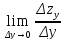
Полный дифференциал функции z=f(x,y) - главная линейная относительно 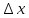и ∆у часть приращения функции ∆z в точке (х,у).

dz=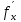(x,y)dx+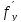(x,y)dy

Если функция f(x,y) определена в некоторой области D, то её частные производные f’x(x,y), f’y(x,y), тоже будут определены в той же области или её части. Будем называть эти производные производными I-ого порядка. Производные этих функций производными II-ого порядка.

; ;

; .

Продолжая дифференцировать полученные равенства, получим частные производные более высоких порядков.

5. Экстремум функции двух переменных: необходимое и достаточное условия.

Точка max М₀ – это если для функции z=f(x,y), определённой в некоторой области, в некоторой окрестности точки М₀(х₀,у₀), верно неравенство f(x₀,y₀)≥f(x,y)

Точка min М₀ – это если для функции z=f(x,y), определённой в некоторой области, в некоторой окрестности точки М₀(х₀,у₀), верно неравенство f(x₀,y₀)≤f(x,y)

Необходимое условие: если функция f(x,y) в точке (х₀,у₀) имеет экстремум, то в этой точке либо обе её частные производные первого порядка равны 0

f´_y(x₀,y₀)=0, f´_x(x₀,y₀)=0,

либо хотя бы одна из них не существует. Эту точку (х₀, у₀) будут называть критической точкой.

Достаточное условие: пусть в окрестности критической точки (х₀,у₀) функция f(x,y) имеет непрерывные частные производные до второго порядка включительно.

Рассмотрим выражение:

1. Если ∆(х₀,у₀)>0, то в точке (х₀, у₀) функция f(x,y) имеет экстремум,

Если (x₀, y₀)<0 – max, если 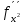(x₀, y₀)>0 – min.

2. Если ∆(х₀,у₀)<0, то в точке (х₀,у₀) функция f(x,y) не имеет экстремума.

3. Если ∆=0, вывод о наличии экстремума сделать нельзя.
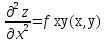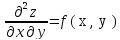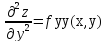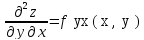