Оценка автокорреляции остатков по модели авторегрессии

Рассмотренный ранее критерий Дарбина — Уотсона не применим для моделей авторегрессии, содержащих в составе объясняющих переменных лаговые значения зависимой переменной. Связано это с тем, что критерий Дарбина — Уотсона для модели авторегрессии может принимать значение, близкое к двум, как при отсутствии, так и при наличии автокорреляции остатков.

Предположим, что в модели авторегрессии (5.51) имеет место автокорреляция остатков, т.е. случайное отклонение можно рассматривать как авторегрессию вида

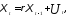(5.56)

где ρ — коэффициент автокорреляции первого порядка; Ut — случайная составляющая.

Тогда уравнение (5.51) можно представить как

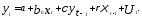(5.57)

В уравнении (5.57) 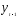связан с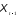как и по уравнению (5.51)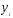связан с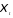. Таким образом, имеется систематическая связь лаговой зависимой переменной со случайной компонентой. Применение теста Дарбина — Уотсона к модели (5.57) может показать отсутствие автокорреляции в остаткахUtпри наличии ее для остатков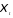. В связи с этим Дж. Дарбин предложил для моделей авторегрессии при оценке существенности автокорреляции остатков использовать другой критерий, который в литературе получил название

h-статистика Дарбина:

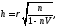(5.58)

где ρ — коэффициент автокорреляции в остатках первого порядка, который практически используется при расчете критерия Дарбина — Уотсона, т.е.

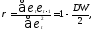
n— число наблюдений в модели; V — выборочная дисперсия коэффициента при лаговой зависимой переменной.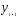

При большом числе наблюдений и при отсутствии в остатках автокорреляции первого порядка h-статистика Дарбина подчиняется стандартизированному нормальному распределению, Поэтому фактическое значениеhсравнивается с табличным по заданному уровню значимости α. Если |h| больше критического значения, то нулевая гипотеза об отсутствии автокорреляции ошибок отклоняется. При практических расчетах чаще всего α берется как 0,05 и если |h| > 1,96, то гипотеза об отсутствии автокорреляции остатков отвергается.

Из уравнения (15) следует, что h-статистика не применима, если величина (nV) > 1. Кроме того, данный критерий предназначен для больших выборок (например, дляn> 30).h-статистика зависит от квадрата стандартной ошибки параметра только при лаговой зависимой переменной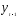(V) и не зависит от числа лагов, используемых в модели авторегрессии.

В рассматриваемом примере автокорреляция остатков не устранена, о чем свидетельствует h-статистики Дарбина: коэффициент автокорреляции в остатках ρ составил 0,440; стандартная ошибка коэффициента регрессии при переменной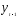оказалась равной 0,1635 (0,7946/4,86); соответственноV= 0,02673 и приn=23, что больше необходимого 1,96.

Автокорреляция в остатках по авторегрессионным моделям может быть устранена с помощью авторегрессионных преобразований с использованием моделей ARMA иARIMA.

Авторегрессионные процессы и их моделирование (общая характеристика) Авторегрессионные процессы

Рассмотренные ранее модели авторегрессии содержали в правой части наряду с лаговыми зависимыми переменными 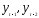и т.д. независимые переменныех. Авторегрессионная модель, в которой отсутствуют независимые переменные иy_tрассмат­ривается как линейная функция только предыдущих своих зна­чений, представляет собойавторегрессионный процесс

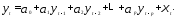(5.59)

В зависимости от того, сколько предыдущих уровней вре­менного ряда включено в уравнение (5.59), авторегрессионный процесс может быть разного порядка. Если текущее значение уровня динамического ряда 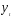рассматривается как линей­ная функция от одного предыдущего значения, то имеем дело с авторегрессионным процессом первого порядка (AR(1), что обычно в англоязычной литературе обозначается какAR(1).

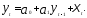(5.60)

Процессы ARмогут быть стационарными и нестационарными. Чтобы процесс был стационарным, коэффициенты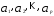в модели (5.59) должны образовывать сходящийся ряд и все кор­ни характеристического уравнения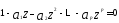(вещественные и комплексные) должны лежать вне единич­ного круга, т.е..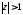

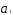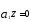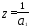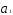Рассмотренное условие стационарности для процесса AR(1) означает, что в уравнении (5.60) параметрдолжен соответствовать величине |а| < 1, так как характеристическое уравнение 1-имеет кореньи |z|>lпри ||<1.

Авторегрессионный процесс с большим числом лагов пред­полагает очень длинные динамические ряды, которые дале­ко не всегда имеются в эконометрических исследованиях.

При наличии коротких временных рядов стационарные AR - процессы могут иметь место после удаления из уровней ряда тенденции и сезонных колебаний. Это означает, что иссле­дователь должен вычленить эти компоненты динамического ряда и подвергать дальнейшей обработке остаточные вели­чины.В этом случае авторегрессионный процесс первого по­рядкаAR(1) примет вид

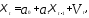(5.61)

где 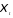— остатки после устранения из уровней ряда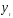тенденции и периодической составляющей;V_t— белый шум.