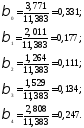- •«Российская таможенная академия»
- •План чтения лекции №1
- •«Российская таможенная академия»
- •Понятие «эконометрика»
- •Формулировки определений понятия «эконометрика»
- •Задачи эконометрики
- •Эконометрическая модель
- •Задачи эконометрическoго моделирования
- •Классы эконометрических моделей
- •Типы данных и виды переменных в эконометрическом моделировании Типы данных
- •Виды переменных
- •Этапы эконометрического моделирования
- •Модели парной регрессии
- •Множественная регрессия. Мультиколлинеарность данных
- •3.2. Отбор факторов при построении множественной регрессии
- •3.2.1. Требования к факторам
- •3.2.2. Мультиколлинеарность
- •3.3. Выбор формы уравнения регрессии
- •3.4. Оценка параметров уравнения линейной
- •3.5. Качество оценок мнк линейной множественной регрессии. Теорема Гаусса-Маркова
- •3.6. Проверка качества уравнения регрессии. F-критерий Фишера
- •3.7. Точность коэффициентов регрессии. Доверительные интервалы
- •3.8 Прогнозирование по модели множественной регрессии
- •3.9 Гетероскедастичность случайных остатков
- •3.10. Обобщенный метод наименьших квадратов
- •3.11. Фиктивные переменные
- •3.12. Тест Чоу
- •Системы одновременных уравнений
- •4.1. Структурная и приведённая форма модели
- •4.2. Оценивание параметров структурной модели
- •Методы оценивания структурных уравнений различных видов
- •1. Точная идентифицируемость
- •2.Сверхидентифицируемость
- •3.Неидентифицируемость
- •Порядковое условие идентификации
- •Ненулевое ограничение
- •3. Анализ методов оценивания
- •Моделирование изолированного динамического ряда
- •Компоненты динамического ряда
- •Выявление и характеристика основной тенденции развития
- •Экспоненциальное сглаживание.
- •Моделирование основной тенденции
- •Статистическое изучение сезонных колебаний
- •Автокорреляция уровней динамического ряда и характеристика его структуры
- •3; 1; 2; 1; 2; 1; 3; 3; 2; 3; 1; 2; 1; 1; 3; 3; 2; 2; 1; 3; 3; 2; 2; 3; 1; 2; 2; 1; 3; 1.
- •Специфика изучения взаимосвязей по рядам динамики
- •Методы исключения тенденции
- •Метод последовательных разностей
- •Метод отклонений от тренда
- •Включение в модель регрессии фактора времени
- •Обобщенный метод наименьших квадратов при построении модели регрессии по временным рядам
- •Модели с лаговыми переменными
- •Модели с распределенными лагами
- •Метод Койка
- •Модели авторегрессии
- •Интерпретация параметров модели авторегрессии
- •Инструментальные переменные как метод оценивания параметров модели авторегрессии
- •Оценка автокорреляции остатков по модели авторегрессии
- •Авторегрессионные процессы и их моделирование (общая характеристика) Авторегрессионные процессы
- •Модели скользящей средней
- •Модели arma
- •Модели arima
- •Методология построения модели arima для исследуемого временного ряда включает следующую последовательность шагов.
- •Кластерный анализ
Модели с распределенными лагами
Интерпретация параметров модели с распределенными лагами
Модели с распределенными лагами бывают двух типов:
— с конечным числом лагов
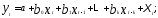 (5.38)
(5.38)
— с бесконечным числом лагов
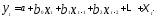 (5.39)
(5.39)
Практическое применение чаще имеют модели с конечным числом лагов, т.е. модели, в которых число лагов экспериментально определено.
Предположим, рассматривается модель,
в которой k= 4, т.е.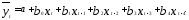 Данная модель означает, что изменение
во времениtобъясняющей
переменнойхбудет влиять на
значения результативного признака в
течение 4-х следующих моментов времени.
Данная модель означает, что изменение
во времениtобъясняющей
переменнойхбудет влиять на
значения результативного признака в
течение 4-х следующих моментов времени.
Коэффициент b0 называют
краткосрочным мультипликатором, так
как он характеризует среднее изменение
результата упри изменении
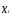 на 1 ед. своего измерения в фиксированный
момент времениt.
на 1 ед. своего измерения в фиксированный
момент времениt.
В момент времени (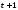 )
воздействие объясняющей переменнойхна результату составит (
)
воздействие объясняющей переменнойхна результату составит (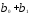 )
единиц, а в момент времени (t+ 2) общее
изменение составит
)
единиц, а в момент времени (t+ 2) общее
изменение составит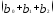 единиц.
единиц.
Любую сумму коэффициентов
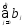 ,
гдеh<kназываютпромежуточным
мультипликатором, а сумму всех
коэффициентов регрессии
,
гдеh<kназываютпромежуточным
мультипликатором, а сумму всех
коэффициентов регрессии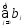 —долгосрочным мультиплипликатором,
который характеризует общее изменениеучерезkинтервалов времени под воздействием
измененияхв моментtна 1 ед.
—долгосрочным мультиплипликатором,
который характеризует общее изменениеучерезkинтервалов времени под воздействием
измененияхв моментtна 1 ед.
При k = 4долгосрочный
мультипликатор составит (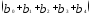 .
Он характеризует общее среднее изменениеучерез четыре временных
интервала при увеличениихв
момент времениt на 1 ед., а
промежуточные мультипликаторы
.
Он характеризует общее среднее изменениеучерез четыре временных
интервала при увеличениихв
момент времениt на 1 ед., а
промежуточные мультипликаторы
(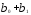 )
— изменение в момент времени (t+
1);
)
— изменение в момент времени (t+
1);
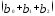 — изменение в момент времени (t+
2);
— изменение в момент времени (t+
2);
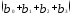 — изменение в момент времени (t+
3).
— изменение в момент времени (t+
3).
Если все коэффициенты регрессии имеют
одинаковые знаки, т.е. характеризуются
однонаправленным изменением yв исследуемыеkмоментов
времени, то можно определить относительные
коэффициенты модели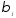 ,
т.е.
,
т.е.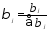 ,
где
,
где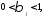 a
a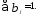 Иными словами,
Иными словами,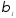 характеризует долю общего измененияyв момент времени
(t + j).
характеризует долю общего измененияyв момент времени
(t + j).
Предположим, что регрессия основных
производственных фондов (у — в млн.
руб.) в зависимости от размера инвестиций
(х — в млн. руб.) характеризуется
уравнением
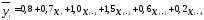 ,
где t — года.
,
где t — года.
Анализ уравнения показывает, что рост инвестиций на 1 млн руб. в текущем периоде приводит к росту основных производственных фондов:
— в том же периоде — на 0,7 млн. руб. (краткосрочный мультипликатор);
— через 1 год — на 0,7 + 1 = 1,7 млн. руб.;
— через 2 года — на 0,7 + 1 + 1,5 = 3,2 млн. руб.;
— через 3 года — на 3,8 млн. руб. (промежуточный, как и предыдущие два, мультипликатор);
— через 4 года — на 4 млн. руб. (долгосрочный мультипликатор).
Относительные коэффициенты модели составят
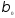 =
0,7/4 = 0,175;
=
0,7/4 = 0,175;
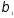 =
1/4 = 0,25;
=
1/4 = 0,25;
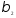 =
1,5/4 = 0,375;
=
1,5/4 = 0,375;
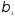 =
0,6/4 = 0,15;
=
0,6/4 = 0,15;
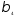 =
0,2/4 = 0,05.
=
0,2/4 = 0,05.
Следовательно, в текущем году реализуется 17,5% воздействия увеличения инвестиций на рост основных производственных фондов, а через год — еще 25%. Через 2 года — еще 37,5%, через 3 года — еще 15% и через 4 года — еще 5%.
Относительные коэффициенты модели
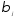 можно использовать как весовые
коэффициенты для расчета средней
величины лага по средней арифметической:
можно использовать как весовые
коэффициенты для расчета средней
величины лага по средней арифметической:
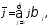
где j— величина лага.
Величина
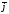 показывает средний интервал времени,
в течение которого будет происходить
изменение зависимой переменнойупод
воздействием изменения объясняющей
переменнойхв момент времениt. Чем меньше величина среднего
лага, тем быстрее реагирует результатуна изменениех. И
наоборот, высокое значение среднего
лага показывает, что воздействие
объясняющей переменной на результат
будет сказываться с течением длительного
промежутка времени. В рассматриваемом
примере величина среднего лага составит
показывает средний интервал времени,
в течение которого будет происходить
изменение зависимой переменнойупод
воздействием изменения объясняющей
переменнойхв момент времениt. Чем меньше величина среднего
лага, тем быстрее реагирует результатуна изменениех. И
наоборот, высокое значение среднего
лага показывает, что воздействие
объясняющей переменной на результат
будет сказываться с течением длительного
промежутка времени. В рассматриваемом
примере величина среднего лага составит
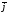 = 0
= 0 0,175 + 1
0,175 + 1 0,25 + 2
0,25 + 2 0,375 + 3
0,375 + 3 0,15 + 4
0,15 + 4 0,05 = 1,65 года.
0,05 = 1,65 года.
Следовательно, основная часть эффекта
увеличения инвестиций проявляется
через 1,65 года. Кроме среднего лага можно
рассчитывать медианный лаг
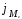 , т.е. тот период времени, в течение
которого с момента времениtбудет реализована половина общего
эффекта воздействия объясняющей
переменнойхна результату.
Для медианного лага справедливо
равенство
, т.е. тот период времени, в течение
которого с момента времениtбудет реализована половина общего
эффекта воздействия объясняющей
переменнойхна результату.
Для медианного лага справедливо
равенство
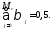
В нашем примере медианный лаг составляет 2 года, т.е. увеличение инвестиций в период времени t на 1 млн. руб. приводит к росту размера основных производственных фондов через 2 года на величину, составляющую половину долгосрочного мультипликатора, т.е. на 2 млн руб. Наибольший аналитический интерес представляет расчет величины медианного лага для моделей с большим числом лаговых переменных.
Оценка параметров моделей с распределенными лагами
Модель с конечным числом лагов при правильной ее спецификации может быть оценена обычным МНК. В этом случае в уравнении
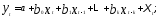 (5.40)
(5.40)
переменные
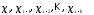 рассматриваются как объясняющие
переменные обычной множественной
регрессии.
рассматриваются как объясняющие
переменные обычной множественной
регрессии.
Вместе с тем применение МНК к моделям с конечным числом лагов может быть реально затруднено ввиду следующих причин:
1) при наличии тенденции переменные
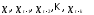 тесно связаны между собой, что вызывает
мультиколлинеарность факторов, которая
может привести к не интерпретируемым
знакам у коэффициентов регрессии и к
снижению их точности;
тесно связаны между собой, что вызывает
мультиколлинеарность факторов, которая
может привести к не интерпретируемым
знакам у коэффициентов регрессии и к
снижению их точности;
2) возможна автокорреляция остатков, так как МНК применяется к временным рядам с тенденцией.
Поэтому нередко для оценки параметров модели с распределенным конечным числом лагов используются специальные методы преобразования, как и для модели с бесконечным числом лагов. Разработаны разные методы оценивания параметров моделей с распределенными лагами, которые учитывают характер распределения коэффициентов регрессии при лаговых объясняющих переменных. Иными словами, методы оценивания параметров модели с распределенными лагами основаны на изучении структуры лага. Так, предполагая полиномиальное распределение лаговых коэффициентов, используют метод Алмон, а при гипотезе геометрической прогрессии для лаговых коэффициентов применяется преобразование Койка.
Полиномиально распределенные лаги Алмон
В 1965 г. III. Алмон предложила способ оценки
параметров модели с распределенными
лагами на основе гипотезы о том, что
лаговые коэффициенты регрессии
аппроксимируются полиномом соответствующей
степени от величины лага. Это значит,
что в модели
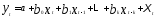 параметр
параметр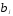 рассматривается как функция:
рассматривается как функция: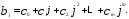 При этом априори выдвигается предположение
о степени полинома. Как правило,
используется многочлен невысокой
степени (m≤ 4).
При этом априори выдвигается предположение
о степени полинома. Как правило,
используется многочлен невысокой
степени (m≤ 4).
Предположим, что
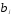 имеет распределение в виде параболы
второй степени, т.е.
имеет распределение в виде параболы
второй степени, т.е.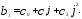 Тогда каждый из коэффициентов
Тогда каждый из коэффициентов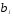 можно представить в виде
можно представить в виде
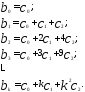
Подставим эти соотношения для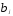 в модель с распределенными лагами и
перегруппируем слагаемые с одинаковыми
значениями с:
в модель с распределенными лагами и
перегруппируем слагаемые с одинаковыми
значениями с:
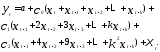
Будем рассматривать слагаемые в скобках
при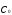 ,
,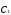 и
и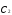 как новые переменныеz,
т.е. модель с распределенными лагами
примет вид
как новые переменныеz,
т.е. модель с распределенными лагами
примет вид
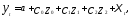
где
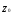 ,
,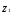 и
и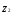 определяются как
определяются как
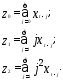
Оценка параметров при преобразованных
переменных z реализуется традиционным
МНК. При этом случайные отклонения
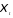 удовлетворяют предпосылкам МНК. Далее
на основе параметров
удовлетворяют предпосылкам МНК. Далее
на основе параметров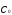 ,
,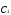 и
и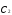 переходим к оценке параметров
переходим к оценке параметров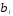 ,
используя выражения коэффициентов
,
используя выражения коэффициентов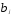 через коэффициенты полинома:
через коэффициенты полинома:
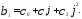
В матричном виде можно записать, что b = Hc, где
 -
матрица весов при лаговых коэффициентах
-
матрица весов при лаговых коэффициентах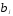 ;
с — вектор коэффициентов при переменных
z.
;
с — вектор коэффициентов при переменных
z.
Тогда модель в целом принимает вид у
= ХНс +
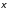 = Zc +
= Zc +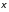 .
.
Стандартная ошибка коэффициентов
регрессии при лаговых переменных
определится как
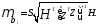
Далее через t-критерий Стьюдента
оценивается значимость коэффициентов
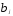 .
.
Качество модели оценивается через
коэффициент детерминации
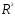 для уравнения регрессии
для уравнения регрессии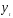 от преобразованных переменныхz,
т.е. по модели
от преобразованных переменныхz,
т.е. по модели
у = Zc +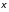 .
.
Таким образом, применение метода Алмон включает в себя следующие этапы работы:
1) определение максимальной величины лага k;
2) определение степени полинома m,
описывающего распределение коэффициентов
регрессии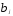 в зависимости от величины лага;
в зависимости от величины лага;
3) расчет преобразованных переменных z;
4) расчет параметров линейной регрессии
уот преобразованных переменныхz, т.е. оценка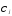 ;
;
5) переход к исходным параметрам
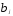 модели с распределенными лагами.
модели с распределенными лагами.
Теоретически достаточно сложно определить максимальную величину лага к. В основном для этой цели используется экспериментальный путь: строится уравнение с большим числом последовательных лагов и с постепенным его уменьшением изучается значимость коэффициентов регрессии при лаговых объясняющих переменных. Останавливаются на варианте, для которого все коэффициенты регрессии статистически значимы.
Степень полинома задается исследователем, исходя из соответствующих теоретических соображений и результатов предыдущих исследований.
Пример 5.6
По данным за 32 квартала об объеме продукции (у — в млн. руб.) и инвестициях в основной капитал (х — в млн. руб.) строится модель с распределенными лагами
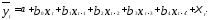 (5.41)
(5.41)
Объем продукции и инвестиции в основной капитал
Таблица 5.13.
|
Номер квартала |
|
|
|
|
|
|
|
|
| |||||||||
|
1 |
5,2 |
0,87 |
|
|
|
|
|
|
| |||||||||
|
2 |
5,6 |
0,9 |
0,87 |
|
|
|
|
|
| |||||||||
|
3 |
6,5 |
1,05 |
0,9 |
0,87 |
|
|
|
|
| |||||||||
|
4 |
6,4 |
1,04 |
1,05 |
0,9 |
0,87 |
— |
— |
— |
— | |||||||||
|
5 |
6,5 |
1,05 |
1,04 |
1,05 |
0,9 |
0,87 |
4,91 |
9,32 |
27,26 | |||||||||
|
6 |
7 |
1,08 |
1,05 |
1,04 |
1,05 |
0,9 |
5,12 |
9,88 |
29,06 | |||||||||
|
7 |
7,4 |
1,12 |
1,08 |
1,05 |
1,04 |
1,05 |
5,34 |
1,05 |
31,44 | |||||||||
|
8 |
7,8 |
1,16 |
1,12 |
1,08 |
1,05 |
1,04 |
5,45 |
10,59 |
31,53 | |||||||||
|
9 |
8,1 |
1,17 |
1,16 |
1,12 |
1,08 |
1,05 |
5,58 |
10,84 |
32,16 | |||||||||
|
10 |
8 |
1,14 |
1,17 |
1,16 |
1,12 |
1,08 |
5,67 |
11,17 |
33,17 | |||||||||
|
11 |
8,5 |
1,17 |
1,14 |
1,17 |
1,16 |
1,12 |
5,76 |
11,44 |
34,18 | |||||||||
|
12 |
8,6 |
1,2 |
1,17 |
1,14 |
1,17 |
1,16 |
5,84 |
11,6 |
34,82 | |||||||||
|
13 |
8,8 |
1,2 |
1,2 |
1,17 |
1,14 |
1,17 |
5,88 |
11,64 |
34,86 | |||||||||
|
14 |
8,9 |
1,24 |
1,2 |
1,2 |
1,17 |
1,14 |
5,95 |
11,67 |
34,77 | |||||||||
|
15 |
8,9 |
1,22 |
1,24 |
1,2 |
1,2 |
1,17 |
6,03 |
11,92 |
35,56 | |||||||||
|
16 |
9,3 |
1,26 |
1,22 |
1,24 |
1,2 |
1,2 |
6,12 |
12,1 |
36,18 | |||||||||
|
17 |
9,4 |
1,23 |
1,26 |
1,22 |
1,24 |
1,2 |
6,15 |
12,22 |
36,5 | |||||||||
|
18 |
9,3 |
1,23 |
1,23 |
1,26 |
1,22 |
1,24 |
6,18 |
12,37 |
37,09 | |||||||||
|
19 |
9,6 |
1,26 |
1,23 |
1,23 |
1,26 |
1,22 |
6,2 |
12,35 |
37,01 | |||||||||
|
20 |
9,7 |
1,28 |
1,26 |
1,23 |
1,23 |
1,26 |
6,26 |
12,45 |
37,41 | |||||||||
|
21 |
9,7 |
1,3 |
1,28 |
1,26 |
1,23 |
1,23 |
6,3 |
12,41 |
37,07 | |||||||||
|
22 |
9,8 |
1,32 |
1,3 |
1,28 |
1,26 |
1,23 |
6,39 |
12,56 |
37,44 | |||||||||
|
23 |
10 |
1,32 |
1,32 |
1,3 |
1,28 |
1,26 |
6,48 |
12,8 |
38,2 | |||||||||
|
24 |
10,2 |
1,33 |
1,32 |
1,32 |
1,3 |
1,28 |
6,55 |
12,98 |
38,78 | |||||||||
|
25 |
10,3 |
1,33 |
1,33 |
1,32 |
1,32 |
1,3 |
6,6 |
13,13 |
39,29 | |||||||||
|
26 |
10,4 |
1,35 |
1,33 |
1,33 |
1,32 |
1,32 |
6,65 |
13,23 |
39,65 | |||||||||
|
27 |
10,5 |
1,35 |
1,35 |
1,33 |
1,33 |
1,32 |
6,68 |
13,28 |
39,76 | |||||||||
|
28 |
10,6 |
1,36 |
1,35 |
1,35 |
1,33 |
1,33 |
6,72 |
13,36 |
40 | |||||||||
|
29 |
10,5 |
1,32 |
1,36 |
1,35 |
1,35 |
1,33 |
6,71 |
13,43 |
40,19 | |||||||||
|
30 |
10,6 |
1,35 |
1,32 |
1,36 |
1,35 |
1,35 |
6,73 |
13,49 |
40,51 | |||||||||
|
31 |
10,7 |
1,38 |
1,35 |
1,32 |
1,36 |
1,35 |
6,76 |
13,47 |
40,47 | |||||||||
|
32 |
11 |
1,4 |
1,38 |
1,35 |
1,32 |
1,36 |
6,81 |
13,48 |
40,42 |
Предполагая квадратичную зависимость
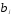 от величины лага
от величины лага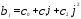 имеем
соотношения
имеем
соотношения
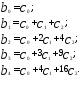 (5.42)
(5.42)
Соответственно модель с распределенными лагами примет вид
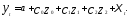
Расчет преобразованных переменных z,- представлен в табл., где
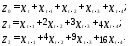
Применяя к преобразованным данным обычный МНК, получим следующее уравнение:
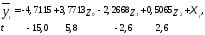
Все параметры уравнения статистически
значимы (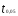 ;df= 26).
;df= 26).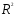 = 0,9955 указывает на хорошее качество
модели.
= 0,9955 указывает на хорошее качество
модели.
Далее найдем коэффициенты регрессии
исходной модели, т.е.
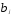 ,
используя выражения (5.42):
,
используя выражения (5.42):
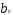 =3,7713;
=3,7713;
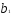 =
3,7713 + (-2,2668) + 0,5065 = 2,011;
=
3,7713 + (-2,2668) + 0,5065 = 2,011;
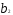 = 3,7713 - 2 • 2.2668 + 4 • 0,5065 = 1,2637;
= 3,7713 - 2 • 2.2668 + 4 • 0,5065 = 1,2637;
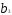 = 3,7713 - 3 • 2,2668 + 9 • 0,5065 = 1,5294;
= 3,7713 - 3 • 2,2668 + 9 • 0,5065 = 1,5294;
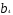 = 3,7713 - 4 • 2,2668 +16 • 0,5065 = 2,8081.
= 3,7713 - 4 • 2,2668 +16 • 0,5065 = 2,8081.
Модель регрессии с распределенными лагами примет вид
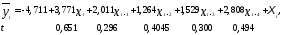
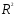 =
0,9955.
=
0,9955.
Для свободного члена астандартная ошибка составила 0,313. Соответственно по t-критерию Стьюдента все параметры оказались статистически значимыми.
Модель показывает, что рост инвестиций в текущем периоде на 100 тыс. руб. способствует росту объема продукции в том же периоде в среднем на 377 тыс. руб., а через квартал — на 578 тыс. руб. В целом же через год прирост объема продукции за счет роста инвестиций на 100 тыс. руб. ожидается в размере 1,138 млн руб. (3,771 + 2,011 + 1,264 + 1,529 + 2,808 = 11,383).
Определив относительные коэффициенты
регрессии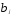 увидим, что половина воздействия фактора
на результат реализуется с лагом в один
квартал:
увидим, что половина воздействия фактора
на результат реализуется с лагом в один
квартал: